以下都是个人理解,刚刚有点理解,所以可能表达不清楚……但是又想把一些理解表达出来,故写了这篇
上篇文章说了,拉格朗日乘子法,可以在等式约数的条件下,求得某函数f的极大或极小值,但是,等式约束只是不等式约束中的特例,如果我们遇到了不等式约束,该怎么办呢?(其实理解了拉格朗日乘子法后,KTT就贼NM简单了)
本文不打算怎么放图了,感觉完全可以接着上一篇继续搞!
首先,对于等式约数,我们可以看成我们自变量可以取的点组成的几条线,也就是约束函数在某高度上的等高线。不过约束换成了不等式约束以后,此时约束就可能由“线”变成了面。
但是,看上去需要考虑的取值变多了,其实不然:
其实把约束由等式变为不等式,对于每个不等式约束,我们要处理的也只有两种情况:
- 要优化函数的极小值点就在约束内
- 要优化函数的极小值点在约束外
第一种情况最好处理——直接无视掉,因为:既然极小值都在约束内了,那么这个约束就如同虚设一般。
第二种情况呢?都已经知道极值在约束外头了,那就不可能往约束里面找了,所以我们至于要考虑约束的边界,其实就是那条熟悉的等高线……所以对于第二种情况,我们可以转化为等式约束的求极值,也就是用前一章所说的东西解决、、、
但是还有问题:我怎么知道极小值是在约束内还是约束外……
其实这个问题挺好解决的,不过首先我们需要把所有的约束条件都统一一下,比如统一改成 g ( x , y , . . . ) < = 0 g(x,y,…)<=0 g(x,y,...)<=0的形式,至于为什么、、、一会就清楚了
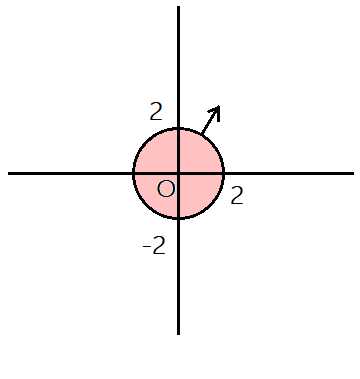
先看看约束吧,比如对于一个约束 g ( x , y ) < = 0 g(x,y)<=0 g(x,y)<=0,我们先看看它的边界,也就是 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0,随机取一个满足条件的 ( x , y ) (x,y) (x,y),求 g ( x , y ) g(x,y) g(x,y)在这里的梯度。由于我们的约束都统一过,所以不难想象,这时的梯度向量的方向肯定是指向约束外而不是约束内
比如图中浅红色区域代表 g ( x , y ) = x 2 + y 2 − 4 < = 0 g(x,y) = x^2+y^2-4<=0 g(x,y)=x2+y2−4<=0,黑圆就是约束边界,箭头是梯度向量,根据约束来看,边界的高度(值)都是0,如果继续顺着梯度走,那么肯定会跳出约束范围,所以梯度指向为约束外。
然后我们再考虑要优化函数在约束边界任意一点的梯度方向,如果梯度方向和约束的梯度方向夹角都小于90度,也就是都指向约束外面,则要优化函数的极小值一定在约束内(该约束可以忽略),反之则在约束外。
OK,现在我们可以来看看怎么求得极值了、
设 F ( x , y , . . . ) = f ( x , y , . . . ) + ∑ λ i g i ( x , y , . . . ) F(x,y,…) = f (x,y,…)+ \sum \lambda_i g_i(x,y,…) F(x,y,...)=f(x,y,...)+∑λigi(x,y,...)
首先,不等式约束可以间接为等式约束,并且可行解一定在约束边界上
则有 ▽ f + ∑ λ i ▽ g i = 0 \bigtriangledown f + \sum \lambda_i \bigtriangledown g_i = 0 ▽f+∑λi▽gi=0,也就是我们上一篇说的梯度共线。
不过需要满足: λ i g i = 0 \lambda_i g_i=0 λigi=0
解释如下:
上面说了,对于某个约束,可行解可能落在约束内,也可能落在约束外。
如果落在约束内,则这个约束可以忽略掉,此时令 λ i = 0 \lambda_i=0 λi=0约去这个约束;而如果可行解在约束外,此时我们要考虑的是约束边界,此时有 g ( x , y , . . . ) = 0 g(x,y,…) = 0 g(x,y,...)=0
总结一下就是 λ i g i = 0 \lambda_i g_i=0 λigi=0
对于 λ i \lambda_i λi还有一些限制,因为要求梯度共线,所以目标函数梯度方向和约束函数的梯度方向只能相同和相反,结合上面所说,只有这两个向量夹角大于90度(此时也就是共线,方向相反),这个约束才有用,故有 λ i > 0 \lambda_i >0 λi>0 ,而刚才说了可行解可能落在约束内有 λ i = 0 \lambda_i =0 λi=0 ,总结一下就是 λ i > = 0 \lambda_i>=0 λi>=0
总的来看:对于
m i n x f ( x , . . . ) s . t .    h i ( x ) = 0 , i = 1 , 2 , 3 , . . . , m .           g j ( x ) ⩽ 0 , j = 1 , 2 , 3 , . . . , n \underset{x}{min} f(x,…) \\ s.t.\: \: h_i(x) = 0 , i = 1,2,3,…,m\\ . \, \: \: \: \: \; \; g_j(x) \leqslant 0 , j = 1,2,3,…,n xminf(x,...)s.t.hi(x)=0,i=1,2,3,...,m.gj(x)⩽0,j=1,2,3,...,n
设 F ( x , μ , λ ) = f ( x ) + ∑ μ i h i ( x ) + ∑ λ j g j ( x ) F(x,\mu ,\lambda )=f(x) + \sum \mu _i h_i(x) + \sum \lambda _j g_j(x) F(x,μ,λ)=f(x)+∑μihi(x)+∑λjgj(x)
解方程:
{ ▽ x F ( x , μ , λ ) = 0 h i ( x ) = 0               g j ( x ) ⩽ 0               λ j g j = 0                     λ j ⩾ 0                     \left\{\begin{matrix} \bigtriangledown_x F(x,\mu ,\lambda ) = 0 \\ h_i(x) = 0\: \: \: \: \: \: \: \: \: \: \: \: \: \\ g_j(x) \leqslant 0 \: \: \: \: \: \: \: \: \: \: \: \: \: \\ \lambda_j g_j = 0 \: \: \: \: \: \: \, \, \, \, \, \, \, \, \, \, \, \, \: \\ \lambda_j \geqslant 0 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:\: \end{matrix}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧▽xF(x,μ,λ)=0hi(x)=0gj(x)⩽0λjgj=0λj⩾0
例子:
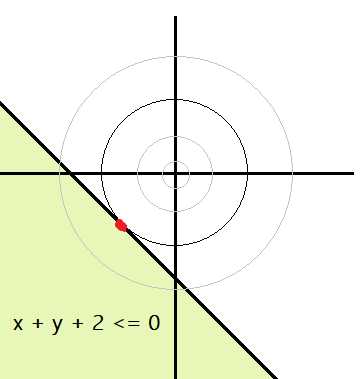
对于 m i n   min\: min f ( x , y ) = x 2 + y 2 f(x,y) = x^2 + y^2 f(x,y)=x2+y2, s . t .    s.t. \: \: s.t. h ( x , y ) = x + y + 2 ⩽ 0 h(x,y) = x + y + 2 \leqslant 0 h(x,y)=x+y+2⩽0,
设 F = f + λ h F = f + \lambda h F=f+λh
则有
∂ F ∂ x = ∂ f ∂ x + ∂ g ∂ x = 2 x + λ = 0 \frac{\partial F}{\partial x} = \frac{\partial f}{\partial x} + \frac{\partial g}{\partial x} = 2x + \lambda = 0 ∂x∂F=∂x∂f+∂x∂g=2x+λ=0
∂ F ∂ y = ∂ f ∂ y + ∂ g ∂ y = 2 y + λ = 0 \frac{\partial F}{\partial y} = \frac{\partial f}{\partial y} + \frac{\partial g}{\partial y} = 2y + \lambda = 0 ∂y∂F=∂y∂f+∂y∂g=2y+λ=0
解得 x = y x = y x=y
则 x + y + 2 = 2 x + 2 ⩽ 0 ⇒ x ⩽ − 1 x + y + 2 = 2x + 2 \leqslant 0 \Rightarrow x \leqslant -1 x+y+2=2x+2⩽0⇒x⩽−1
且要满足 λ h = 0 \lambda h = 0 λh=0,且 λ = − 2 x \lambda = – 2x λ=−2x。故 − 2 x × ( 2 x + 2 ) = 0 -2x \times (2x + 2) = 0 −2x×(2x+2)=0
解得 { x = 0 ( 舍 去 )      x = − 1 ( 满 足 ) \left\{\begin{matrix} x = 0 (舍去) \:\:\:\: \\ x = -1(满足) \end{matrix}\right. {
x=0(舍去)x=−1(满足)
且 λ = 2 ⩾ 0 \lambda = 2 \geqslant 0 λ=2⩾0
故在 x = − 1 , y = − 1 x = -1, y = -1 x=−1,y=−1时, f ( x , y ) = ( − 1 ) 2 + ( − 1 ) 2 = 2 f(x,y) = (-1)^2 + (-1)^2 = 2 f(x,y)=(−1)2+(−1)2=2为所求极小值
参考资料:
约束优化方法之拉格朗日乘子法与KKT条件
今天的文章KTT条件_kkt算法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/71031.html