彻底理解0-1背包问题

0-1背包问题

给定$n$个重量为$w_1$，$w_2$，$w_3$，…，$w_n$，价值为$v_1$，$v_2$，$v_3$，…，$v_n$的物品和容量为$C$的背包，求这些物品中一个最有价值的子集，使得在满足背包的容量的前提下，包内的物品总价值最大

注：0-1背包问题指的是每个物品只能使用一次

V1.0——递归方法

首先我们用最容易理解的递归方法来尝试解决这个问题

我们用$F(n,C)$表示将前$n$个物品放进容量为$C$的背包里，得到的最大的价值。

我们从自顶向下的角度来看，假如我们已经进行到了最后一步（即求解将第$n$个物品放到背包所获得的最大价值），此时我们便有两种选择

1. 不放第$n$个物品，此时总价值为$F(n-1,C)$
2. 放置第$n$个物品，此时总价值为$v_n+F(n-1,C-w_n)$

两种选择中总价值最大的方案就是我们的最终方案，递推式（有时也称之为状态转移方程）如下

$$F(i,C)=max(F(i-1,C),v(i)+F(i-1,C-w(i)))$$

编程实现如下：

public class KnapSackV1 { 
   
    /** * 解决背包问题的递归函数 * * @param w 物品的重量数组 * @param v 物品的价值数组 * @param index 当前待选择的物品索引 * @param capacity 当前背包有效容量 * @return 最大价值 */
    private static int solveKS(int[] w, int[] v, int index, int capacity) { 
   
        
        //基准条件：如果索引无效或者容量不足，直接返回当前价值0
        if (index < 0 || capacity <= 0)
            return 0;

        //不放第index个物品所得价值
        int res = solveKS(w, v, index - 1, capacity);
        
        //放第index个物品所得价值（前提是：第index个物品可以放得下）
        if (w[index] <= capacity) { 
   
            res = Math.max(res, v[index] + solveKS(w, v, index - 1, capacity - w[index]));
        }
        return res;
    }

    public static int knapSack(int[] w, int[] v, int C) { 
   
        int size = w.length;
        return solveKS(w, v, size - 1, C);
    }

    public static void main(String[] args){ 
   
        int[] w = { 
   2,1,3,2};
        int[] v = { 
   12,10,20,15};
        System.out.println(knapSack(w,v,5));
    }
}

V2.0——记忆化搜索

我们用递归方法可以很简单的实现以上代码，但是有个严重的问题就是，直接采用自顶向下的递归算法会导致要不止一次的解决公共子问题，因此效率是相当低下的。

我们可以将已经求得的子问题的结果保存下来，这样对子问题只会求解一次，这便是记忆化搜索。

下面在上述代码的基础上加上记忆化搜索

public class KnapSack01 { 
   

    private static int[][] memo;

    /** * 解决背包问题的递归函数 * * @param w 物品的重量数组 * @param v 物品的价值数组 * @param index 当前待选择的物品索引 * @param capacity 当前背包有效容量 * @return 最大价值 */
    private static int solveKS(int[] w, int[] v, int index, int capacity) { 
   
        //基准条件：如果索引无效或者容量不足，直接返回当前价值0
        if (index < 0 || capacity <= 0)
            return 0;

        //如果此子问题已经求解过，则直接返回上次求解的结果
        if (memo[index][capacity] != 0) { 
   
            return memo[index][capacity];
        }

        //不放第index个物品所得价值
        int res = solveKS(w, v, index - 1, capacity);
        
        //放第index个物品所得价值（前提是：第index个物品可以放得下）
        if (w[index] <= capacity) { 
   
            res = Math.max(res, v[index] + solveKS(w, v, index - 1, capacity - w[index]));
        }
        
        //添加子问题的解，便于下次直接使用
        memo[index][capacity] = res;
        
        return res;
    }

    public static int knapSack(int[] w, int[] v, int C) { 
   
        int size = w.length;
        memo = new int[size][C + 1];
        return solveKS(w, v, size - 1, C);
    }

    public static void main(String[] args) { 
   
        int[] w = { 
   2, 1, 3, 2};
        int[] v = { 
   12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

V3.0——动态规划算法

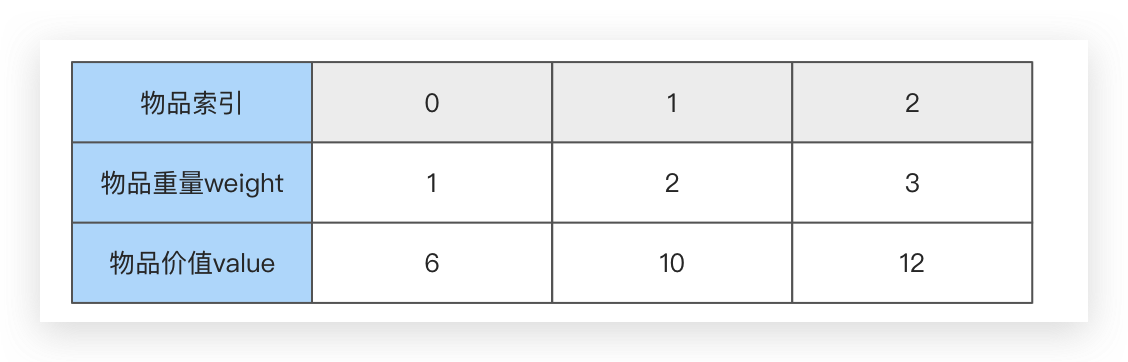
假如我们现在有三个物品，物品的重量和价值如下表所示，背包的最大容量是5

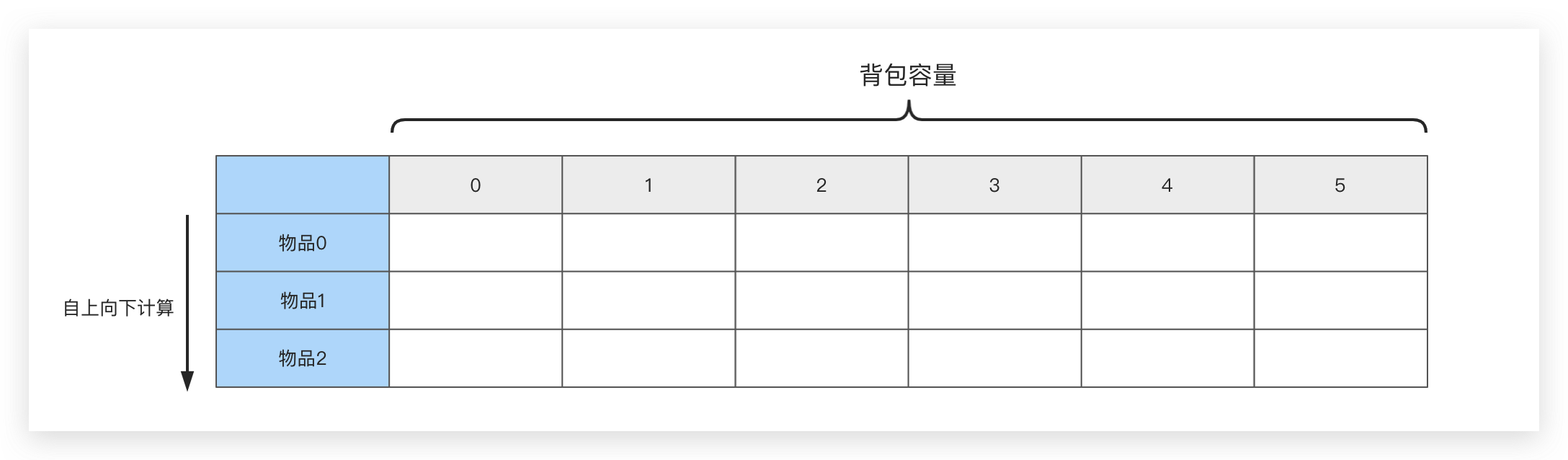
通过上述信息，我们可以得到一张二维表，二维表中每一个空格对应的就是V1.0版本中提到的$F(n,C)$

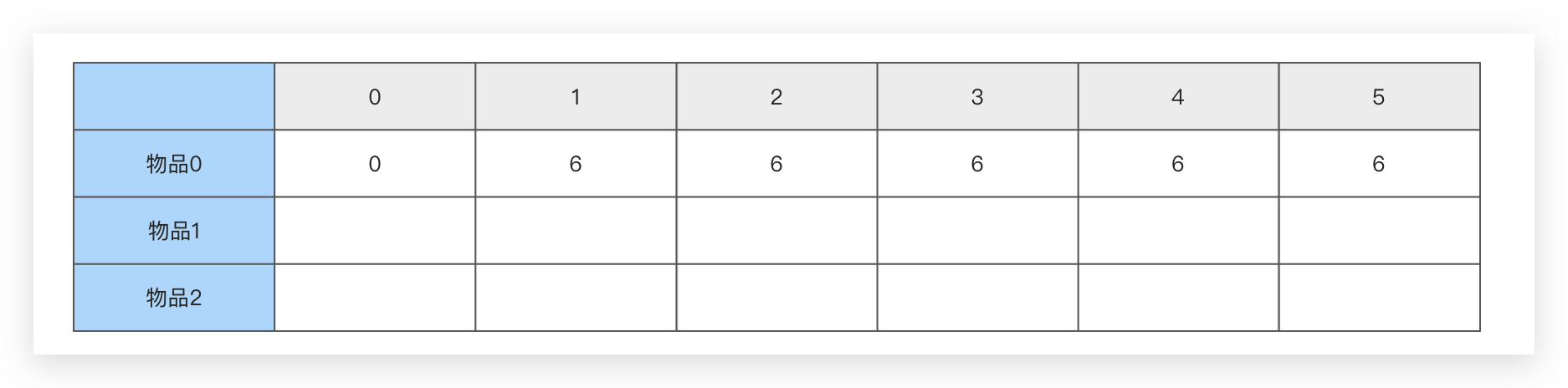
我们可以很轻松地填充二维表的第一行数据，所代表的含义是$F(0,C)$

即在背包容量从0到5时，选择物品0所能获得的最大价值

继续填充第二行数据，此时的含义是，当背包容量从0到5时，待选择物品为物品1时背包的最大价值

注意：我这里说的 不是 选择物品1时 也不是 不选择物品1时的背包最大价值，因为选或不选都有可能

除了第一行以外，其他行的计算都包含当前行物品选或不选的两种可能，按照上文的递推公式来计算

以下图中标记的位置为例，当背包容量为3，待选择为物品1时，此时我们只需要根据之前在表格中填充过的数据进行计算即可，这就是动态规划！

更具体点说，标记位置的值取自下面两种情况的最大值

• 当选择将物品1放入背包时（前提是放得下），此时背包的最大价值为物品1的价值+二维表[0][1]处的值，因为现在的背包容量需要减去物品1所占用的空间（3-2=1）
• 当不选择将物品1放入背包时，此时背包的最大价值为二维表中[0][3]的值

再给大家看一遍递推公式，好好品味一下上面的这个关系，你肯定能搞明白
$$F(i,C)=max(F(i-1,C),v(i)+F(i-1,C-w(i)))$$

public class KnapSack01 { 
   
    public static int knapSack(int[] w, int[] v, int C) { 
   
        int size = w.length;
        if (size == 0) { 
   
            return 0;
        }

        int[][] dp = new int[size][C + 1];
        
        //初始化第一行
        //仅考虑容量为C的背包放第0个物品的情况
        for (int i = 0; i <= C; i++) { 
   
            dp[0][i] = w[0] <= i ? v[0] : 0;
        }
        
		//填充其他行和列
        for (int i = 1; i < size; i++) { 
   
            for (int j = 0; j <= C; j++) { 
   
                dp[i][j] = dp[i - 1][j];
                if (w[i] <= j) { 
   
                    dp[i][j] = Math.max(dp[i][j], v[i] + dp[i - 1][j - w[i]]);
                }
            }
        }
        
        return dp[size - 1][C];
    }

    public static void main(String[] args) { 
   
        int[] w = { 
   2, 1, 3, 2};
        int[] v = { 
   12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

V4.0——动态规划空间复杂度的极致优化

上面的动态规划算法使用了$O(n\ast C)$的空间复杂度（因为我们使用了二维数组来记录子问题的解）

其实我们完全可以只使用一维数组来存放结果，但同时我们需要注意的是，为了防止计算结果被覆盖，我们必须从后向前分别进行计算。为什么呢？往下看。

我们仍然假设背包空间为5，根据
$$F(i,C)=max(F(i-1,C),v(i)+F(i-1,C-w(i)))$$
我们可以知道，当我们利用一维数组进行记忆化的时候，我们只需要使用到当前位置的值和该位置之前的值，举个例子

假设我们要计算$F(i,4)$,我们需要用到的值为$F(i-1,4)$和$F(i-1,4-w(i))$,因此为了防止结果被覆盖，我们需要从后向前依次计算结果

经过V3.0版本的思考，你们画个图就能理解刚才的解释了，给出最终的动态规划代码

public class KnapSack01 { 
   
    public static int knapSack(int[] w, int[] v, int C) { 
   
        int size = w.length;
        if (size == 0) { 
   
            return 0;
        }

        int[] dp = new int[C + 1];
        
        //初始化第一行
        //仅考虑容量为C的背包放第0个物品的情况
        for (int i = 0; i <= C; i++) { 
   
            dp[i] = w[0] <= i ? v[0] : 0;
        }

        for (int i = 1; i < size; i++) { 
   
            for (int j = C; j >= w[i]; j--) { 
   
                dp[j] = Math.max(dp[j], v[i] + dp[j - w[i]]);
            }
        }
        return dp[C];
    }

    public static void main(String[] args) { 
   
        int[] w = { 
   2, 1, 3, 2};
        int[] v = { 
   12, 10, 20, 15};
        System.out.println(knapSack(w, v, 5));
    }
}

利用背包问题的思想解决问题

leetcode 416 Partition Equal Subset Sum

给定一个仅包含正整数的非空数组，确定该数组是否可以分成两部分，要求两部分的和相等

问题分析

该问题我们可以利用背包问题的思想进行求解。

假设给定元素个数为$n$的数组arr，数组元素的和为sum，对应于背包问题，等价于有$n$个物品，每个物品的重量和价值均为为arr[i]，背包的限重为sum/2，求解背包中的物品最大价值为多少？

class Solution { 
   
    private boolean knapSack(int[] nums,int sum){ 
   
        int size = nums.length;
        
        boolean[] dp = new boolean[sum + 1];
        for (int i = 0;i <= sum;i ++){ 
   
           dp[i] = i == nums[0];
        }
        
        for (int i = 1;i < size;i++){ 
   
            for (int j = sum;j >= nums[i];j--){ 
   
                dp[j] = dp[j] || dp[j-nums[i]];
            }
        }
        return dp[sum];
    }
    
    public boolean canPartition(int[] nums) { 
   
        int sum = 0;
        for (int item : nums){ 
   
            sum += item;
        }
        
        //如果数组元素和不是2的倍数，直接返回false
        if (sum % 2 != 0)
            return false;
        
        return knapSack(nums,sum/2);
    }
}

今天的文章彻底理解0-1背包问题分享到此就结束了，感谢您的阅读。