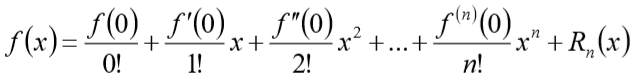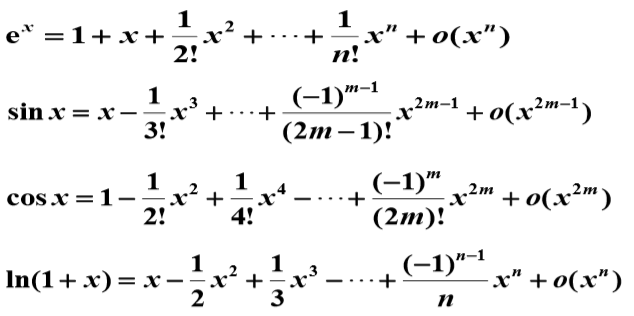比较通俗地讲解一下泰勒公式是什么。
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值
所以泰勒公式是做什么用的?
简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像),注意,逼近的时候一定是从函数图像上的某个点展开。如果一个非常复杂函数,想求其某点的值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。泰勒公式在机器学习中主要应用于梯度迭代。
***********************************************************************************************************************************
***********************************************************************************************************************************
1. 问题的提出
多项式 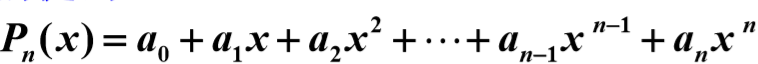
***********************************************************************************************************************************
***********************************************************************************************************************************
2. 近似计算举例
初等数学已经了解到一些函数如: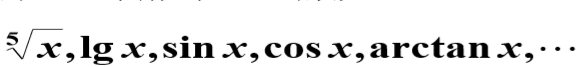

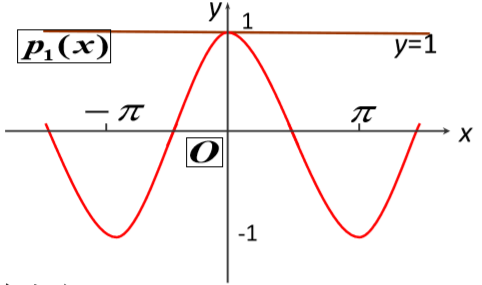
①. 一次(线性)逼近
利用微分近似计算公式 f(x) 











线性逼近优点:形式简单,计算方便;缺点:离原点O越远,近似度越差。
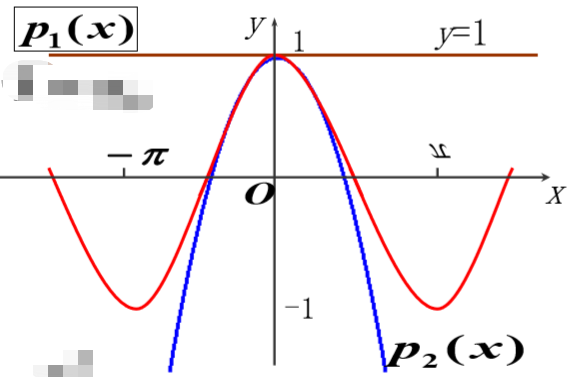
②. 二次逼近
二次多项式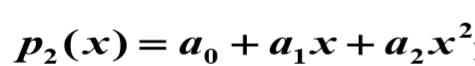














所以 



二次逼近要比线性逼近好得多,但局限于 [ 

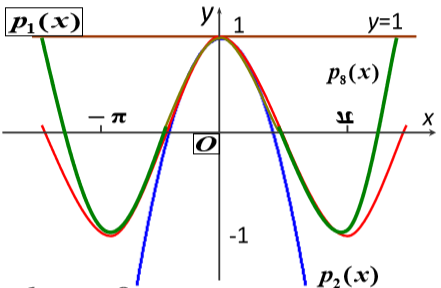
③. 八次逼近
八次多项式 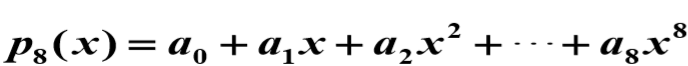





…. …. ….


所以 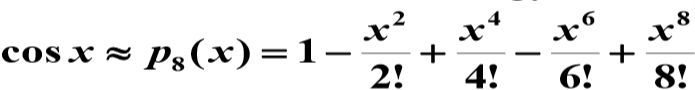


由上述3次不同程度的函数逼近可以看出:对于精确度要求较高且需要估计误差的时候,必须用高次多项式来近似表达函数,同时给出误差公式 。
以上就是利用多项式函数去逼近给定函数的一个过程。
*****************************************************************************************************************************************
*****************************************************************************************************************************************
3. 泰勒公式的推导
由此引出一个问题:给定一个函数 



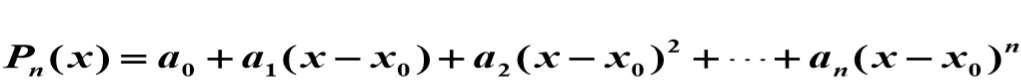




从几何上看,

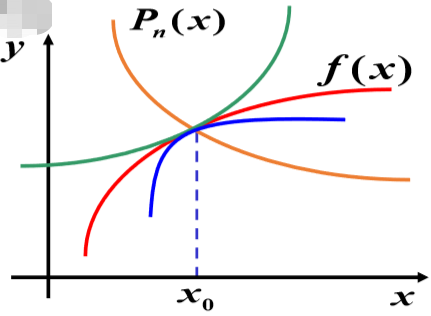
使它们在 
1. 首先要求两曲线在 

2. 如果要靠得更近,还要求两曲线在 


3. 如果还要靠得更近,还要求曲线在 







综上所述,所要找的多项式应满足下列条件:
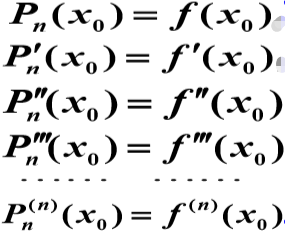

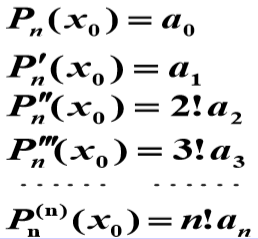

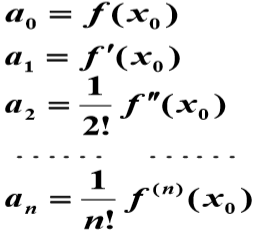
解释一下上面的转换时如何做的,以上面第三行的二阶导数为例:
第一个箭头的转换:将 


第二个箭头的转换:所以 

多项式函数 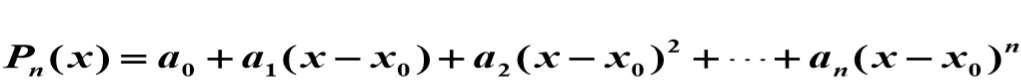


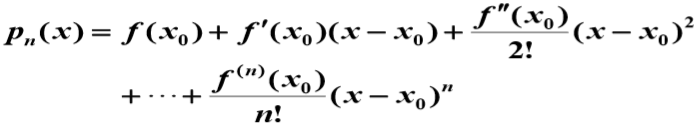

****************************************************************************************************************************************
****************************************************************************************************************************************
4. 泰勒公式的定义
所以我们就得到了泰勒公式的定义:
如果函数 





其中余项 (即误差) 


****************************************************************************************************************************************
****************************************************************************************************************************************
5. 扩展 —— 麦克劳林公式
是泰勒公式的一种特殊情况:即当 

几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
佩亚诺余项为 
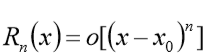
今天的文章泰勒公式展开式大全_八个常见的泰勒公式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/77893.html