叉乘的几何意义_叉乘的本质

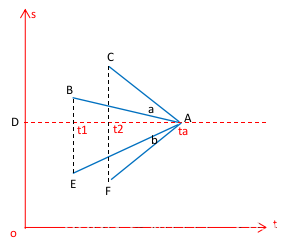
如上图所示：
AB x AC = |AB||AC|sin(a) (a表示AB与AC的夹角），根据叉乘的右手准则，ABx AC的朝向为sot平面的坐标负值方向。
AE x AF = |AE||AF|sin(b) (b表示AE与AF的夹角），根据叉乘的右手准则，AE x AF的朝向为sot平面的坐标正值方向。

其几何意义是：AB x AC的结果为负值，表明B、C两点是按顺时针方向移动；AE x AF的结果为正值，表明E、F两点是按逆时针方向移动。

如果横坐标定义为时间t，纵坐标定义为位移s，且s(t)是t的非单调递减函数，且排除待测试的两个点出现跨越直线DA的情形（即待测试的两个点不能出现类似于E、B这个情形），则其几何意义是：AB x AC的结果为负值，表明B、C两点在A点上方；AE x AF的结果为正值，表明E、F两点在A点下方。

今天的文章叉乘的几何意义_叉乘的本质分享到此就结束了，感谢您的阅读。