研究论文出现的名词,飞速Google、Baidu、Bing等齐上阵。
一、演化博弈理论的概述
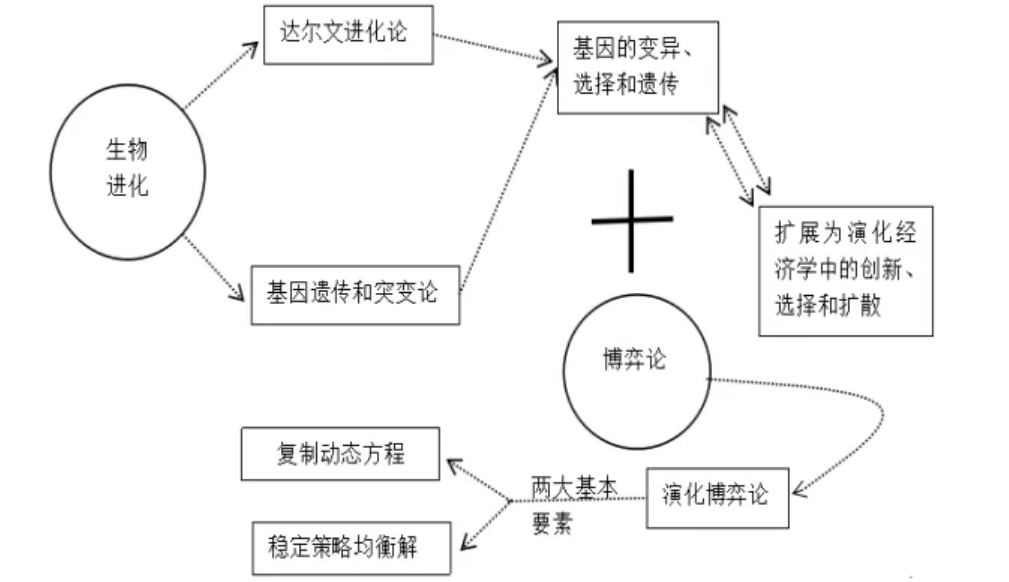
演化博弈理论的英文名是Evolutionary Game Theory。演化博弈理论一般会探讨博弈论在生物学中的应用,尤其是纳什均衡的一种很重要的生物学角度的解释:纳什均衡是无数次动态博弈的稳定状态,也可以说成:物竞天择,适者生存。虽然演化思想最初来自于生物学领域,但演化博弈论和演化经济学都把“创新,选择和扩散”视为演化的主要机制,演化博弈论也为演化经济学提供了微观基础,演化博弈的基本形成如下图:
在传统博弈理论中,常假定参与人是完全理性的,且参与人在完全信息条件下进行的,但在现实的经济生活中的参与人来讲,参与人的完全理性与完全信息的条件是很难实现的。在企业的合作竞争中,参与人之间是有差别的,经济环境与博弈问题本身的复杂性所导致的信息不完全和参与人的有限理性问题也显而易见。
与传统博弈理论不同,演化博弈理论并不要求参与人是完全理性的,也不要求完全信息的条件。演化博弈论是把博弈理论分析和动态演化过程分析结合起来的一种理论。在方法论上,它不同于博弈论将重点放在静态均衡和比较静态均衡上,强调的是一种动态的均衡。演化博弈理论源于生物进化论,它曾相当成功地解释了生物进化过程中的某些现象。如今,经济学家们运用演化博弈论分析社会习惯、规范、制度或体制形成的影响因素以及解释其形成过程,也取得了令人瞩目的成绩。演化博弈论目前成为演化经济学的一个重要分析手段,并逐渐发展成一个经济学的新领域。
二、演化博弈模型的特征
演化博弈模型有如下几个特征:
- 以参与人群体为研究对象,分析动态的演化过程,解释群体为何达到以及如何达到目前的这一状态;
- 群体的演化既有选择过程也有突变过程;
- 经群体选择下来的行为具有一定的惯性。
三、演化博弈理论的两大要素
关于演化博弈的实例可以查看【四、参考文献】中的第 3 条。
3.1 复制动态方程
演化博弈模型中,所构建的复制动态方程的基本形式为:
d x ( t ) d t = [ f ( s i , x ) − f ( x , x ) ] x i \frac{\mathrm{d} x(t)}{\mathrm{d} t} = [f(s_i, x)-f(x,x)]x_i dtdx(t)=[f(si,x)−f(x,x)]xi
其中:
| 符号 | 含义 |
|---|---|
| s i s_i si | 演化群体内博弈的策略集 |
| x i x_i xi | 在 t 时刻下,博弈群体中有多少数量比例的个体选择了策略 s i s_i si |
| f ( s i , x ) f(s_i, x) f(si,x) | 当博弈个体选择 s i s_i si 时,个体的期望支付 |
| f ( x , x ) f(x, x) f(x,x) | 整个群体的平均期望支付 |
3.2 稳定策略均衡解
在演化博弈过程中,博弈双方不再是以稳定的纳什均衡解作为策略最终的选择结构,而是通过一个不断比较、学习和模仿的过程,逐渐去探究演化稳定均衡解。
演化博弈模型的基本形式如下:
| 主体A \ 主体B | 选择 P 1 P_1 P1 策略 | 选择 P 2 P_2 P2 策略 |
|---|---|---|
| 选择 P 1 P_1 P1 策略 | (g, g) | (k, f) |
| 选择 P 2 P_2 P2 策略 | (f, k) | (c, c) |
在这个博弈矩阵中,P1 策略博弈主体的数量比例为 x x x,P2 策略博弈主体的数量比例为 1 − x 1-x 1−x。
其中:
| 符号 | 含义 |
|---|---|
| g g g | 双方都采取 P 1 P_1 P1 策略时的收益 |
| c c c | 双方都采取 P 2 P_2 P2 策略时的收益 |
| k k k | 主体 A 选择了 P 1 P_1 P1 策略,而 B 选择了 P 2 P_2 P2 策略时行为主体 A 的收益 |
| f f f | 主体 A 选择了 P 2 P_2 P2 策略,而 B 选择了 P 1 P_1 P1 策略时行为主体 A 的收益 |
因此,行为主体 A(用 U 1 U_1 U1 代表)和行为主体 B(用 U 2 U_2 U2 代表)各自的收益以及整个博弈群体的平均收益(用 U 代表)满足以下等式。
U 1 = x g + ( 1 − x ) k U 2 = x c + ( 1 − x ) f U = x U 1 + ( 1 − x ) U 2 U_1 = xg + (1-x)k \\ U_2 = xc + (1-x)f \\ U = xU_1 + (1-x)U_2 U1=xg+(1−x)kU2=xc+(1−x)fU=xU1+(1−x)U2
根据演化博弈概念,构建演化博弈的复制动态方程:
F ( x ) = d x d t = x ( U 1 − U ) F(x)=\frac{dx}{dt}=x(U_1-U) F(x)=dtdx=x(U1−U)
通过数理计算可以得出复制动态方程的最终形式为:
F ( x ) = x ( 1 − x ) [ k − f + x ( g − f − k + c ) ] F(x)=x(1-x)[k-f+x(g-f-k+c)] F(x)=x(1−x)[k−f+x(g−f−k+c)]
令复制动态方程结果为零,得出三个解如下:
x 1 = 0 x 2 = 1 x 3 = c − k g − f − k + c x1=0 \\ x2=1 \\ x3=\frac{c-k}{g-f-k+c} x1=0x2=1x3=g−f−k+cc−k
再将这三个解入公式 F ’ ( x ) F’(x) F’(x) 中,即复制动态方程的一阶导方程中。
若 F ’ ( x ) < 0 F’(x)<0 F’(x)<0,则该解就是演化博弈的稳定策略均衡解。
四、参考文献
- 演化博弈理论
- 百度百科:演化博弈理论
- Chapter7:演化博弈论(Evolutionary Game Theory)
今天的文章
演化博弈理论模型_博弈论模型分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/80689.html