gis空间数据的三个基本特征_数据的三个基本特征

3.1 地理空间数据的基本结构

1.地理空间数据定义与特征

空间对象：GIS处理的客体，是现实世界中客观存在的实体或现象。可以抽象成点、线、面、体等多种数据类型。 

● 点对象的表达：相对集中于一个较小范围，且按比例尺缩小后仅能呈点状分布的实体或现象。eg.温度监测站的分布
● 线对象的表达：呈线状或带状分布的实体或动态现象。eg.物流配送线路
● 面对象的表达：分布于较广大范围，且按比例尺缩小后仍能明确显示其轮廓的实体或现象。eg.土地利用类型图
● 体对象的表达：通常用来表示人工或自然的具有长、宽、高的三维目标。eg.三维场景
在GIS中，地理数据是表示地理位置、分布特点的自然现象和社会现象的诸要素文件。它包括自然地理数据和社会经济数据。

地理空间数据的特征：

1. 空间特征：指空间物体的几何特征以及拓扑关系。
2. 属性特征：与空间现象的属性信息相关联。
3. 时间特征：地理空间数据是动态的信息。

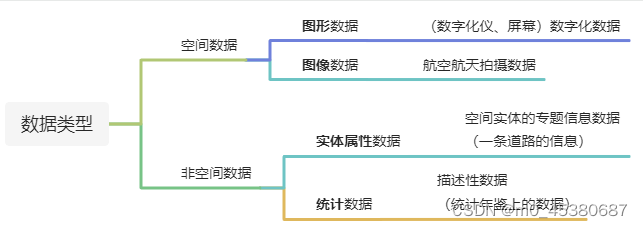
2.地理空间数据的分类

根据数据来源划分为四类

3.地理空间数据结构与组织

图形数据

● 概念：把构成地图要素的点、线、面以点的坐标对(×,y)形式记录下来,形成有规律的数据集合体。
● 来源：纸质地图数字化，空间分析结果，测量获得，图像数据转换获得。
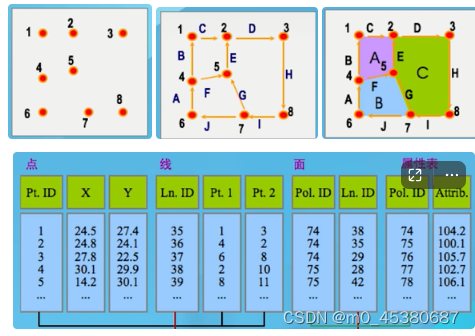
● 表达：
点以单一的坐标对来表示。(“代码”，1，x,Y,)
线以多个坐标对来表示。(“代码”，n，x1,Y1,x2,Y2…xn,Yn)
面以多个坐标对来表示,且最后一个坐标对与第一个坐标对相重合。(“代码”,n,x1,Y1,x2,Y2…xn-1,Yn-1)
● 组织：

● 图形数据的比例尺：反映了制图区域和地图的比例关系。地图上某线段的长度与实地相应线段的水平长度之比，称为地图比例尺。
图上1cm=实地1公里，即地图比例尺为1:。
● 图形数据的拓扑结构：指基本要素点、线、面和体之间具有邻接、关联和包含的拓扑关系，与长度、面积无关。
欧几里德平面上实体对象都具有着拓扑和非拓扑属性。
拓扑属性：

1. 一个点在一个弧段的端点。
2. 一个弧段是一个简单弧段。(自身不相交)
3. 一个点在一个区域的边界上。
4. 一个面的连接性。（任意两点有路径)
   非拓扑属性：●两点之间的距离●弧段的长度●一个区域的周长、面积
   拓扑邻接：存在于空间图形同类要素之间的拓扑关系，如节点邻接关系，多边形邻接关系。eg.湖南与湖北
   拓扑关联：存在于空间图形中不同类要素之间的拓扑关系，如多边形与弧段、弧段与节点之间的关联关系。eg.道路与建筑
   拓扑包含：存在于空间图形中同类但不同级的基本要素之间的拓扑关系。eg.省与市

图像数据

● 概念：图像数据的最小单元为象元或像素，像元的数值可用于描述客观世界中存在的现象。
● 实质：像元的阵列。每个像元由行列号确定其位置，且具有实体属性的编码值。

图像栅格数据是地表一定面积内数据的近似、离散化的表示。
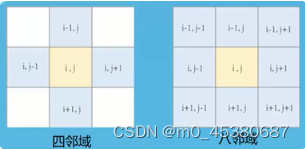
空间分辨率：像素所代表的的地面范围的大小，即扫描仪的瞬时视场，或地面物体能分辨的最小单元。

距离d1<分辨率，不可分辨出两个地物。距离d2>分辨率，可以分辨出两个地物。
● 表达

● 组织形式
1.面向栅格单元：以不同层中对应于同一象元位置上的各个属性值表示为一个数组。
2.面向地理实体：以多边形为单位，记录属性值及组成多边形的各个像元坐标。
3.以“层”方式存储：以层为基础，每层以像元为序，记录其坐标和属性值。
● 方向表达

水文分析应用

3.2 矢量数据的结构特征

1.矢量数据的概念

矢量数据是指通过记录地理实体坐标的方式精确地表示点、线、面等实体的空间位置和形状。

2.矢量数据的编码

数据编码：把需要加工处理的信息，根据一定的数据结构和目标的定性特征，用特定的代码或编码字符表示，以便于计算机识别和管理。eg.矩阵二元映射为数组

编码分类

● 坐标序列法：任何点、线、面实体都可以用某一坐标体系中的坐标点坐标（x,y )来表示。
优点：文件结构简单。易于实现以多边形为单位的运算和显示。
缺点：公共边重复存储，造成冗余和匹配误差。缺少邻域关系信息。不能解决多边形嵌套问题。

● 树状索引编码法：采用树状索引以减少数据冗余并间接表示邻域信息。
优点：消除了相邻多边形边界的数据冗余和不一致。
缺点：获取邻域信息和岛状信息较麻烦，需要查找所有多边形索引文件。

● 拓扑结构编码法：解决多边形嵌套和邻域关系。输入数据的同时输入拓扑连接关系。从一系列相互关联的链建立拓扑结构。

双重独立地图编码系统：DIME(Dual Independent ）数据文件的基本元素是由始末点定义的弧段，复杂的曲线可由多条弧段组成。每条弧段有两个指向结点的指针，和两边多边形的编码。查找组织多边形的各条边界线的效率较低。

3.矢量数据的压缩

● 概念：从所取得的矢量数据集合中抽出一个子集作为一个新的信息源，在规定的精度范围内最好地逼近原集合，而又取得尽可能大的压缩比。
● 原则：最好地逼近原集合（形状、密度、空间关系…）；取得尽可能大的压缩比。
压缩比：表示信息载负量减少的程度

压缩方法

● 间隔取点法：每隔n个点取一点，或每隔一规定的距离取一点，但首末点一定要保留。
● 间隔取点法-按距离取点：没有考虑相邻点对之间的精确关系，可能会遗漏拐点和极值点。

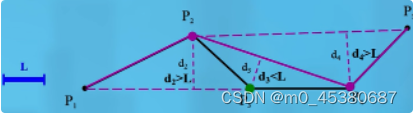
● 垂距法：在给定的曲线上每次顺序取三个点，计算中间点与其它两点连线的垂距d，并与阈值L比较。若大于阈值，则保留该节点，否则删除。（考虑点间距离变化）

● 偏角法：计算连接第一点和第二点，与连接第一点和第三点的矢量间的夹角。如果这个角度超过了预定的角度限差，就保留中间点，否则删除。（考虑点间角度变化）

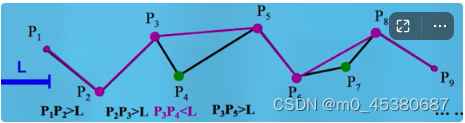
● 光栏法：由点和限差圆盘来定义一个扇形，根据曲线上点是否在扇形区域内来确定取舍

1)以P1为起点，连接P1P2，过P2做P1P2的垂线a1a2，使得a1P2 = a2P2 = L/2，定义扇形区域a1P1a2。

2)判断P3是否在扇形内。若在，舍去P2，连接P1P3，过P3作P1P3的垂线b1b2，使b1P3 = b2P3 = L/2。若b1或b2落在扇形a1P1a2外，则用b1b2与扇形的交点c1或c2代替。定义扇形b1P1c2
3)判断下一个节点是否在扇形内。是，则重复②，直到下一节点在最新定义的扇形外。

4)当发现在扇形外的节点，如图P4，此时保留P3，并以P3为新的起点，重复1—3的步骤。直到整个点列处理完，保留的节点顺序构成新的点列。
● 道格拉斯-普克法:对给定曲线的首末点虚连一条直线，求中间所有点与直线间的距离，并找出最大距离dmax，用dmax与限差L比较:
大则保留对应点，以该点为界将曲线分为两段，对每一段重复使用该方法。小则舍去所有中间点。(整体出发，递归选择曲线弯曲强(转角大)的地方)

优点：选择的点是原始曲线上的点，保证了精度;与原曲线相比，整体位移最小;.与手工综合中选择的关键点基本一致。

4.矢量数据的变换

二维几何图形的变换
点的变换可以由矩阵算子来实现，含有点的坐标矩阵(x,y)和一个一般的2*2的变换矩阵（称之为矩阵算子）相乘的结果是:

平移变换translate：x’( i)=x(i)Tri(xp,yp)。Tri(xp，yp)是平移变换算子，其元素排列形式为∶

比例变换scale：x ‘( i） =x(i)Scl(s 1 , S2)。Scl(S1,S2)为比例变换算子，其元素排列形式为:

S1=S2≠1时，为相似变换
S1=1, S2≠1时，为y方向的变换
S1≠ 1， S2=1时，为x方向的变换
当S1≠ S2≠1时，为x和y方向都变比例，且不等。
旋转变换rotation：x ‘( i ) =x(i)Rot(θ)。θ为旋角，它从x轴正向起算，逆时针为正，顺时针为负，Rot(θ)为旋转变换因子，其矩阵元素排列为∶
即
错移变换：x ‘(i） =x(i)T ( m , n )。m和n方向错移，T( m, n)为错移变换算子，其矩阵元素排列形式为∶

当n=0时，向x方向错移（沿着x的边改变角度）。当m=0时，向y方向错移。

Trl(2,1)，Rot(30° ) , Scl ( 2,2 )，scl ( 2, 1 )
Scl ( 1, 2 ) ，Scl ( 0.5,0.5 )，T(0.5,0),T(0,0.5)
Rot ( -θ )是Rot ( θ )的逆运算，即Rot ( – θ ) ·Rot(θ)=1
Rot -1(θ)=Rot(- θ)。Trl -1(xp, yp)=Trl(-xp , -yp)。Scl -1(S1,S2)=Scl(1/S1,1/S2)

正交矩阵：

3.3 栅格数据的结构特征

1.栅格数据的概念

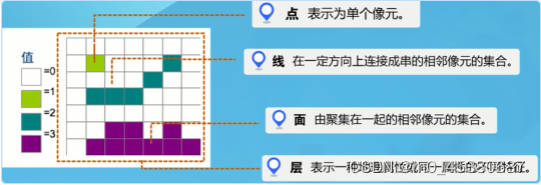
● 概念：把空间分割成统一的尺寸与形状（栅格或格子)的一种空间填充数据结构，整个区域由栅格单元(象元或像素）组成。
● 分层:每个层只能描述一种信息。
● 获取：1.中心归属法，每个栅格单元的值以网格中心点对应的面域属性值来确定。（人口密度分布）
2.面积归属法：值以在该网格单元中占据最大面积的属性值来确定。（城市绿地）
3.长度归属法：值以网格中线的大部分长度所对应的面域的属性值来确定。（地质断裂带）

栅格单元位置和属性值:每个栅格单元都有自己的位置和属性值。
分辨率为50m，X所处的位置为(4,3)，左上角坐标为(1000,1000 )，x’=1000-504=800，y’=1000+503=1150。

2.栅格数据的压缩编码

长度编码法：从左向右，从上至下扫描栅格数据，记录属性值及相同的栅格数目。
改变扫描顺序法：迂回式的读取数据方法，省去每次跳回每行开始处的时间，节省扫描时间。
链式编码/边界链码法:多边形的边界可表示为由某一原点开始并按某些基本方向确定的单位矢量链。缺点：难以实现叠加运算。局部修改将改变整体结构，效率低。相邻边界重复存储。
游程长度编码：按行的顺序存储多边形内的各个像元的列号，即在某行上从左到右存储该多边形的始末像元列号。

特点：在许多相邻像元属性值相同的基础上，压缩效率更高。进行网格加密时，数据量没有明显增加。易于检索、叠加、合并等操作。压缩和解压处理工作都有所增加。
块式编码：将游程长度编码扩大到二维的情况，把多边形范围划分成由像元组成的正方形，然后对各个正方形进行编码。

特点：所能包含的正方形越大，边界越简单，编码的效果越好。在合并、插入、检查延伸性、计算面积等操作时有明显的优越性。对不适应的运算方式，必须再转换成简单数据形式才能顺利进行。
四叉树编码：将2n×2n像元阵列的区域，逐步分解为包含单一类型的方形区域，最小的方形区域为一个像元。（广泛使用）

优点：容易而有效地计算多边形的数量特征。阵列各部分的分辨率是可变的。与简单栅格编码的相互转换较容易。多边形中嵌套不同类型小多边形的表示较方便。
缺点：转换的不确定性，用同一形状和大小的多边形可能得出多种不同的四叉树结构。

3.栅格数据的运算

二值图像：每个像素只有两个可能值（0,1），灰度值没有中间过渡的数字图像。
优点：占用空间少。容易识别图像的结构特征。
缺点：只能描述轮廓，不能描述图像内部细节。
布尔逻辑运算是一种基本运算

宏运算
扩张：描述地理事物的扩张，如城市扩张，污染物扩散。

侵蚀：描述地理事物分布或影响范围的缩小，如农田被侵占。

加粗：

减细运算的原理:加粗“0”象元，但需要添加限制条件，以避免线划断裂或象元消失。
填充:带有边界条件的逐步加粗法

栅格数据重采样：当栅格单元分辨率不一致的情况下，为实现入库或叠加处理，需要使用重采样技术(Resampling)，把不同尺寸的栅格转化为同一种尺寸的栅格。
通常把尺寸较小的栅格转化为较大的尺寸。

3.4 矢量和栅格数据格式的转换

矢量与栅格数据比较
矢量数据 栅格数据
优点 数据结构更加严密，
便于拓扑操作，
图形输出美观。 数据结构简单，叠加操作更易实现、更有效。能有效表达空间可变性。便于进行图像的有效增强。

缺点 数据结构复杂，叠加操作不方便，表达空间变化性能力差，难以实现增强处理。 数据量大，需要压缩。难以表达拓扑关系。图像放大输出不美观，有锯齿。

1.矢量转栅格

点的转换
设点的矢量坐标为(x,y )，转换后栅格单元的行列值分别为Ⅰ和J，则有I=1+INT 〔( y max-y )/dy ] J=1+INT 〔(x- Xmin )/dx 〕

线的转换
某一线段两端点的坐标为（×1，y1 ) ，( x2，y2 ) ，且y2> y1。
线段两端点所在栅格的行列号分别为I，J和I2，J2。
点(xi,yi)为直线段经过的中间栅格的水平中心线与直线段交点的坐标。

多边形的转换
● 扫描算法：沿栅格阵列的行的方向扫描，在每两次遇到多边形边界点的两个位置之间的栅格，属于该多边形。
● 边界代数填充法：对含有多边形信息的弧段文件，沿其前进方向逐栅格搜索。
弧段上行∶弧段左边的栅格点赋值=左多边形特征码-右多边形特征码
弧段下行：弧段左边的栅格点赋值=右多边形特征码-左多边形特征码。

2.栅格转矢量

步骤
step1.图像二值化
step2.细化或提取边界点和节点
step3.边界线跟踪和生成的拓扑关系
目的是将细化处理后的栅格数据，整理为从结点出发的线段或闭合的线条，并以适量形式存储。
step4.删除冗余取点
方法
边界的检索——双边界直接搜索法
让左右多边形信息保存在边界点上，每条边界弧段由两个并行的边界链组成，分别纪录该边界弧段的左右多边形信息。
边界点和节点的提取：

线的细化——剥皮法
每次剥离一个栅格宽的一层像元，直至省下彼此连通的由单个栅格组成的图形。将栅格转换成点，并依次连通，生成线段。

今天的文章
gis空间数据的三个基本特征_数据的三个基本特征分享到此就结束了，感谢您的阅读。