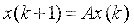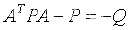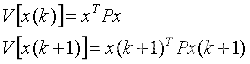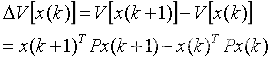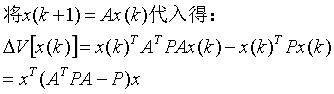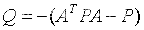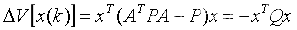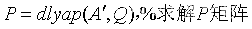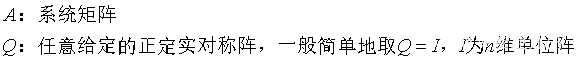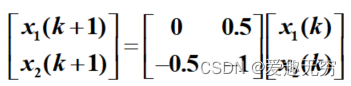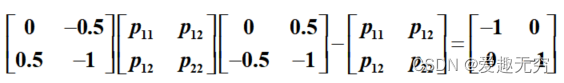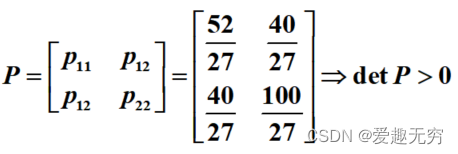离散系统稳定性判据_离散系统的因果性和稳定性

注：Lyapunov稳定性理论主要内容：李雅普诺夫第一方法和第二方法，本篇文章继续上一篇分析线性离散时间系统稳定性，非线性系统稳定性将单独写文章进行分析！敬请关注，谢谢~

一、李雅普诺夫稳定性判定

1.1 Lyapunov两类稳定性方法分析：

（1）Lyapunov渐近稳定的充要条件（第一方法）：A的特征值模均小于1；
（2）Lyapunov渐近稳定的充要条件（第二方法）：对于任意的正定矩阵Q，存在**正定矩阵P**满足Lyapunov方程：

证明：
和连续时间系统一样，取Lyapunov函数为：

则有


与连续时间系统一样，令：

即为Lyapunov方程，则：

只要Q正定，Lyapunov函数变化率为负数，能量随着时间增加肯定逐渐减小至收敛。和连续时间系统一样，一般也是先确定Q，然后求解Lyapunov方程，最后找到正定的P，Q一般取单位阵。

1.2 总结：

二、举例

2.1 MATLAB函数形式：

注意：
同连续时间系统Lyapunov稳定性一样，这里只求解开环系统稳定性，只分析系统矩阵A，还没有涉及到闭环系统反馈矩阵K以及闭环状态状态矩阵A_cl=(A–BK)

2.2 MATLAB函数实例：

eg1. 确定二阶系统在原点处的稳定性


在Lyapunov方程中，取Q =I，得

>> P=[52/27 40/27;40/27 100/27]

P =
    1.9259    1.4815
    1.4815    3.7037

用MATLAB函数dlyap()

>> A=[0 0.5;-0.5 1];Q=eye(2,2)

Q =
    1     0
    0     1

>> P=dlyap(A',Q)

P =
   1.9259   -1.4815
  -1.4815    3.7037

从而系统在原点的平衡状态是大范围渐近稳定的。

eg2. 求线性定常离散时间系统的稳定性条件

eg3. 求线性定常离散时间系统的稳定性条件

>> eig(A)
ans =
    1
    1

A的特征值模均等于1；所以该系统不稳定，Lyapunov方程无解。

>> A=[0.99 0;0 0.99];Q=eye(2,2);dlyap(A',Q)

ans =
  50.2513         0
        0   50.2513
        
>> eig(A)
ans =
   0.9900
   0.9900

A的特征值模均等于1；所以该系统稳定，Lyapunov方程有解。

三、离散Lyapunov方程的解

形式

区别：与第一、二章的区别在于在Q的基础上加了K^TRK

>> A

A =

   1.1000    2.0000
        0    0.9500

>> B

B =

        0
   0.0790
   >> Q

Q =

    1     0
    0     1

>> R

R =

   0.1000

先用离散dlqr()函数求解最优反馈增益矩阵K

[K,P,r] = dlqr(A,B,Q,R)
K =
    2.4950   12.5106

P =
    4.0373    8.5226
    8.5226   31.5400

r =
   0.5308 + 0.2651i
   0.5308 - 0.2651i

① 根据lyapunov方程可知闭环系统矩阵Q2=Q+K^TRK
② 再求解闭环系统矩阵Acl

>> Acl=A-B*K
Acl =
   1.1000    2.0000
  -0.1971   -0.0383

>> eig(Acl)
ans =
  0.5308 + 0.2651i
  0.5308 - 0.2651i

闭环系统矩阵特征值在单位圆内，所以系统稳定
再来求解Lyapunov方程P

>> P=dlyap(Acl',Q2)
P =
 4.0373    8.5226
 8.5226   31.5400

再求解反馈矩阵Kmpc

Q_ =

   1.0000         0         0         0         0         0         0         0
        0    1.0000         0         0         0         0         0         0
        0         0    1.0000         0         0         0         0         0
        0         0         0    1.0000         0         0         0         0
        0         0         0         0    1.0000         0         0         0
        0         0         0         0         0    1.0000         0         0
        0         0         0         0         0         0    4.0373    8.5226
        0         0         0         0         0         0    8.5226   31.5400

>> K_=(Fai'*Q_*Fai+R_)^(-1)*Fai'*Q_*F

K_ =

   2.4950   12.5106
   0.2785    4.5107
  -0.5822    0.3856
  -0.7165   -1.1786

发现第一个k跟dlqr()求出的结果相同

今天的文章离散系统稳定性判据_离散系统的因果性和稳定性分享到此就结束了，感谢您的阅读。