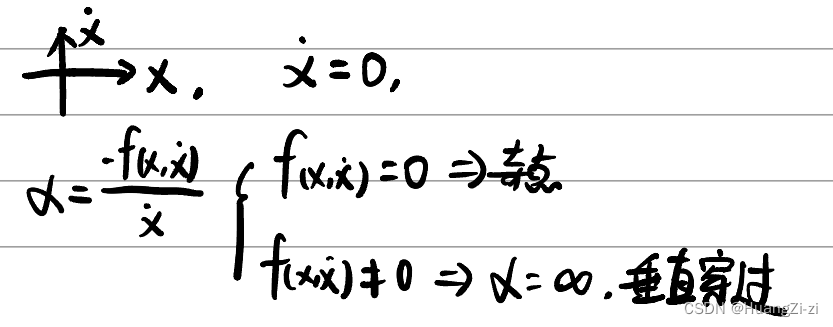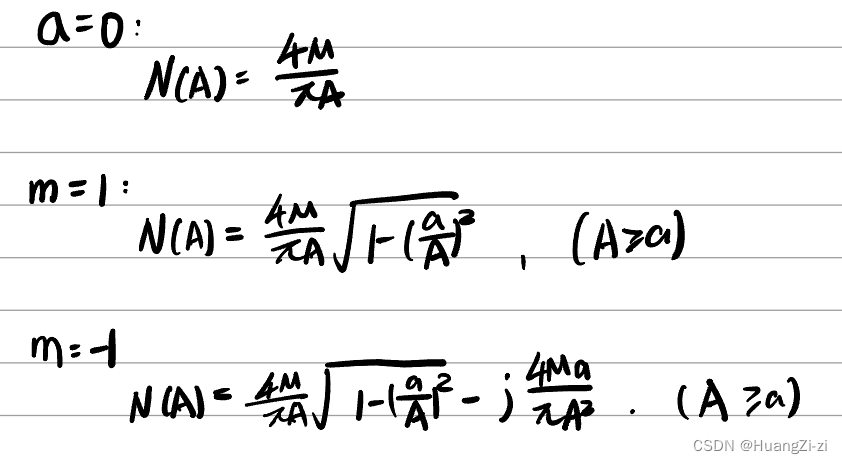本节介绍非线性系统的典型特性
本节介绍相平面法、描述函数法分析非线性系统
文章目录
非线性控制系统概述
- 非线性是普遍规律,广泛存在的。非线性系统运动形式多样,种类繁多
- 线性模型是特殊情况,是实际系统在特定条件下的近似描述
非线性系统的特殊性体现在:
-
不满足叠加原理
-
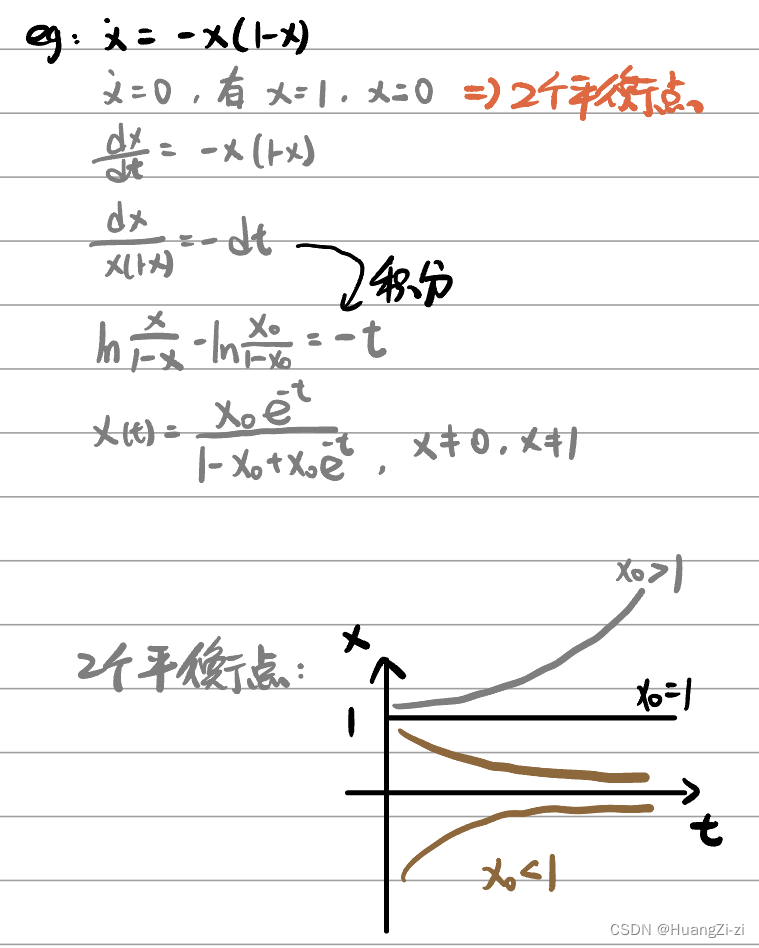
稳定性——不仅与自身结构参数有关,还与输入、初始条件有关。平衡点可能不唯一
-
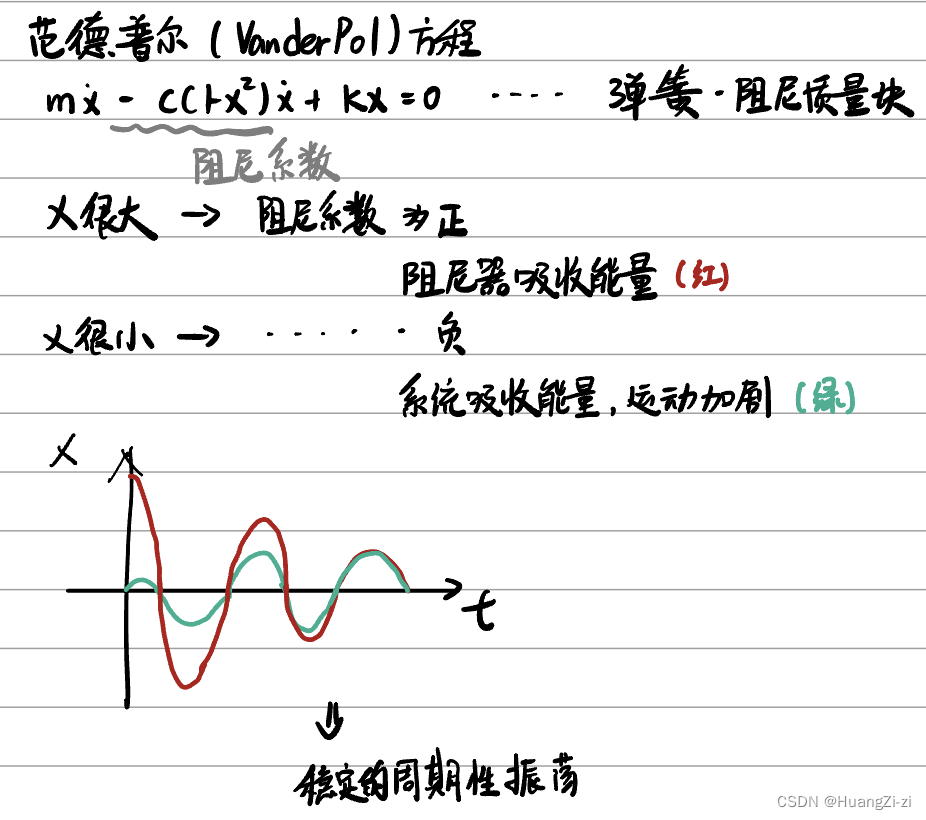
自激震荡——受到外部扰动后,自行维持一个稳定的震荡(区别无阻尼震荡:与输入无关)
-
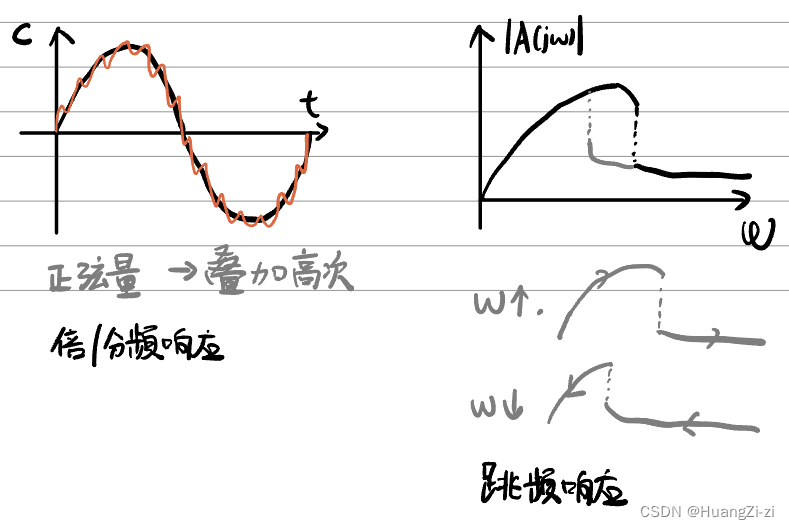
频率响应——畸变、不连续
典型非线性特性
饱和特性
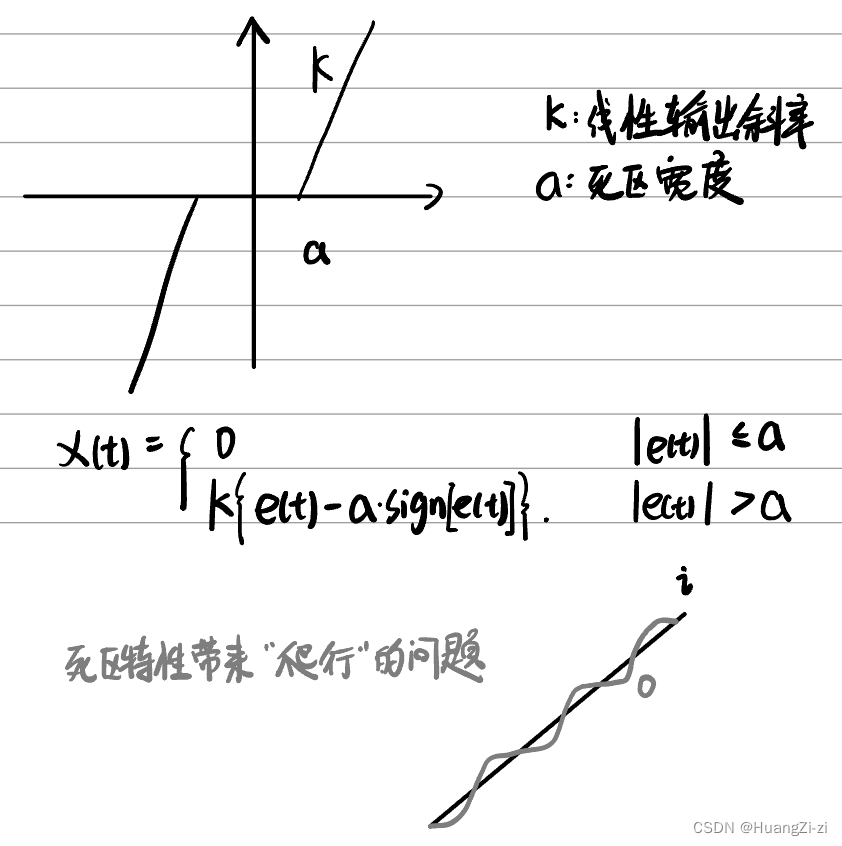
死区特性
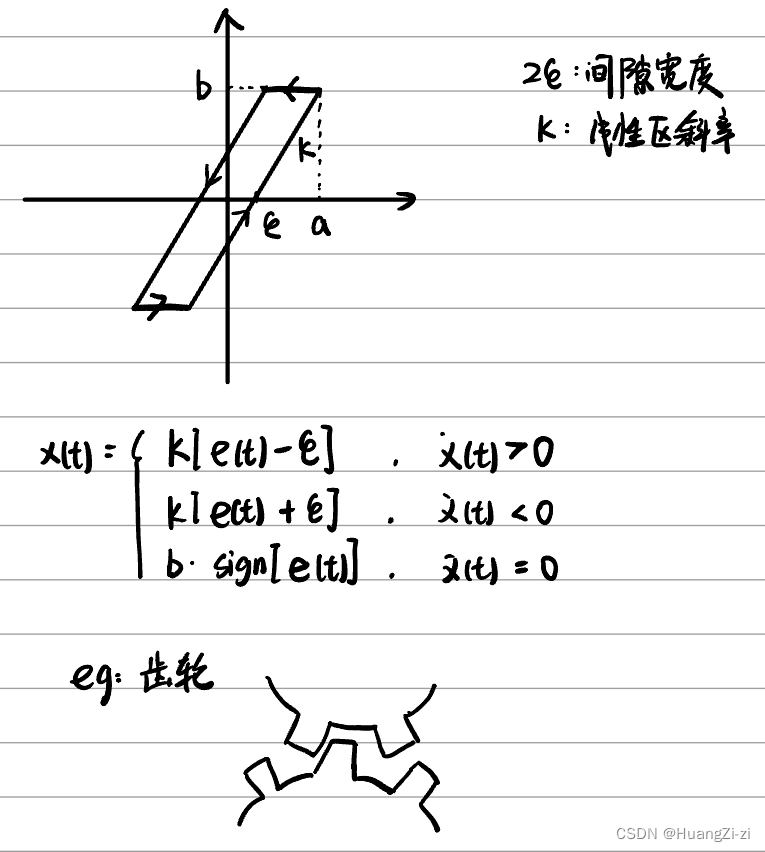
间隙特性
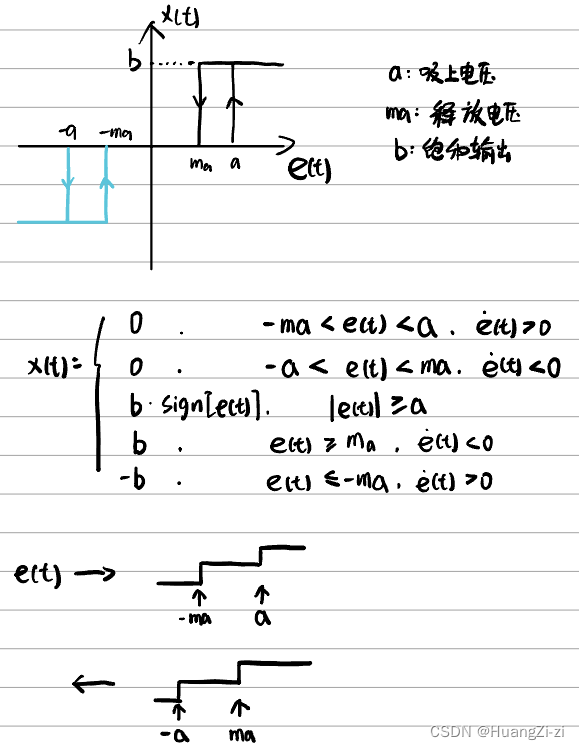
继电器特性
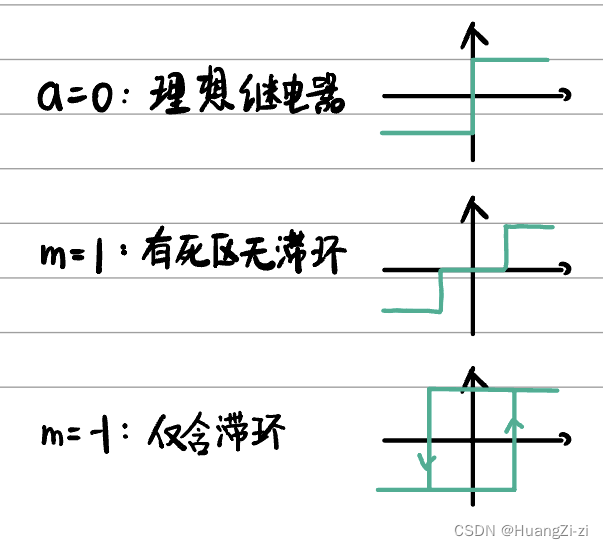
特殊情况:
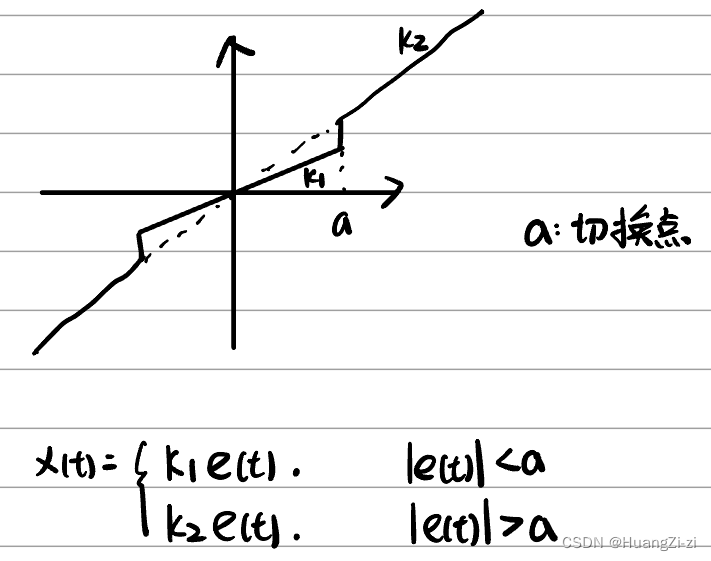
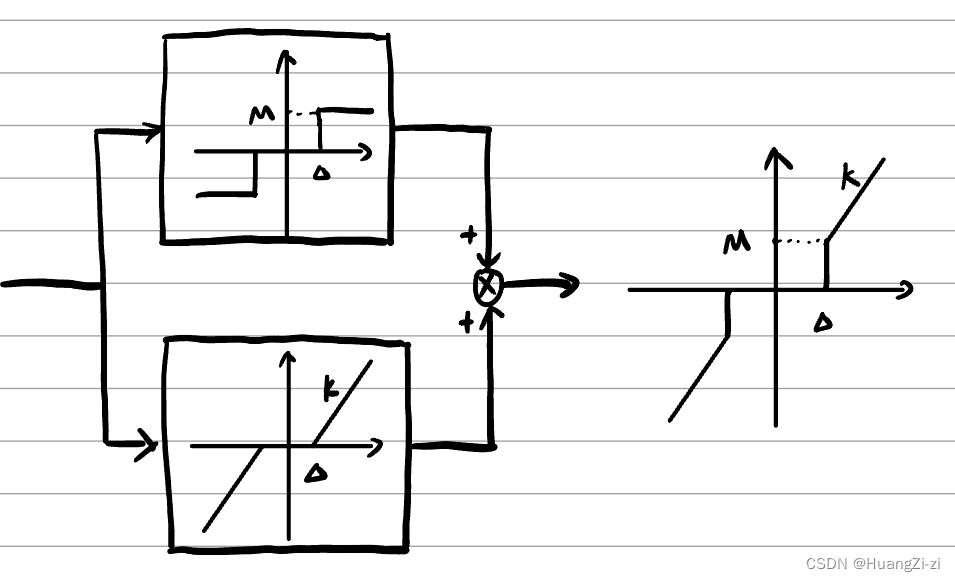
变增益特性
非线性特性的等效变换
- 并联等效
直接叠加就可以
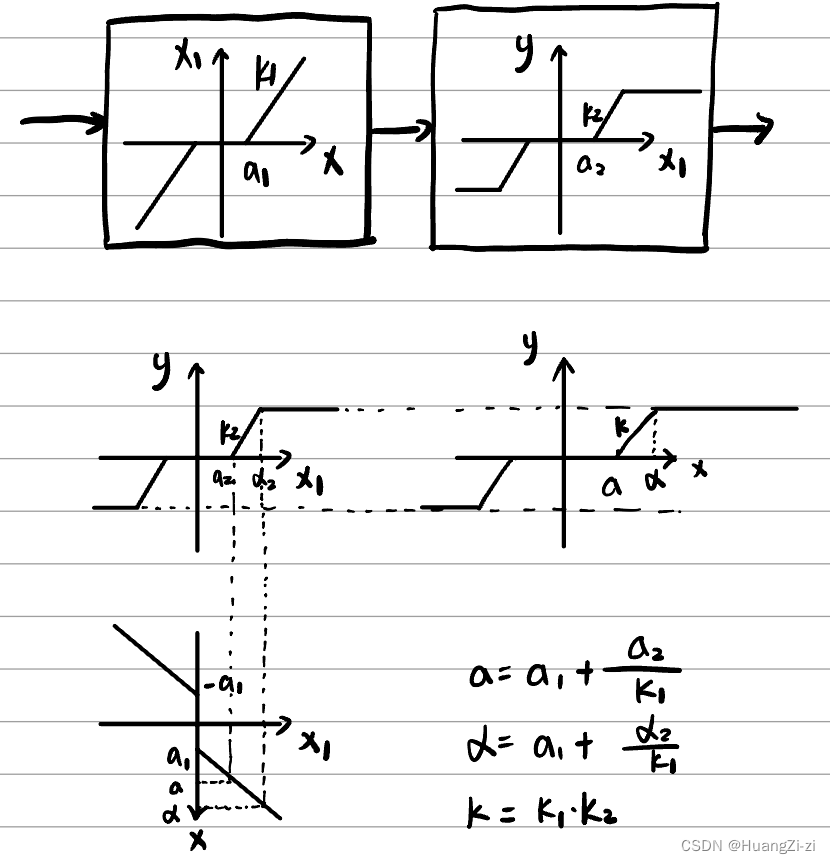
- 串连等效
一方输出作为另一方输入,需画图分析
相平面法
1885年庞加莱提出,用于解决一阶、二阶;线性、非线性系统的问题(平面->两个变量->二阶)
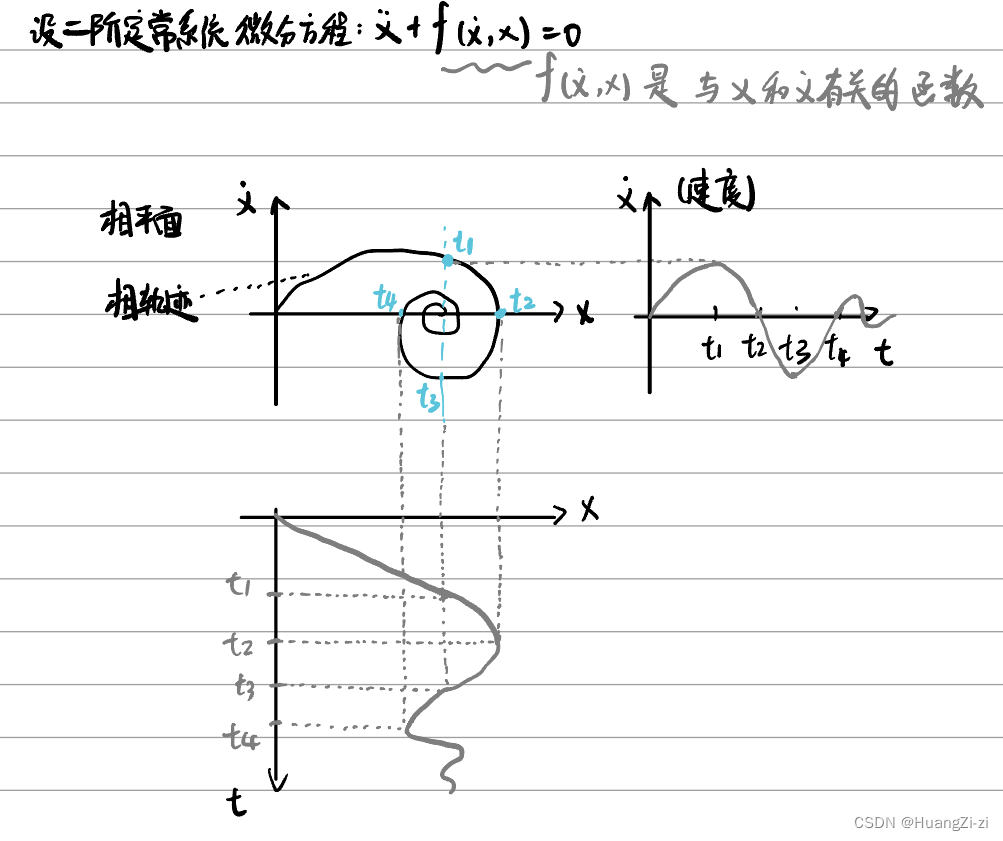
相平面:某参变量及其导数构成的, X ˙ \dot{X} X˙为纵轴, X X X为横轴的平面(X可以为任意一个变量),用于描述系统状态
相轨迹:这个参变量及其导数随时间变化在相平面上描绘出来的轨迹
直观感受一下:
根据 X ˙ \dot{X} X˙和 X X X之间的函数关系可以描绘出相轨迹:
相轨迹里隐藏了时间变量,把时间变量展开就可以看到输出、输出变化速度与时间的关系,进而分析系统了。
相轨迹的性质
-
斜率
-
对称性条件
-
奇点
-
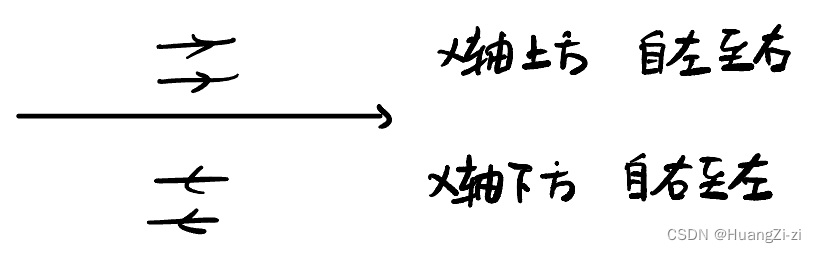
通过X轴的斜率
-
运动方向
相轨迹的绘制
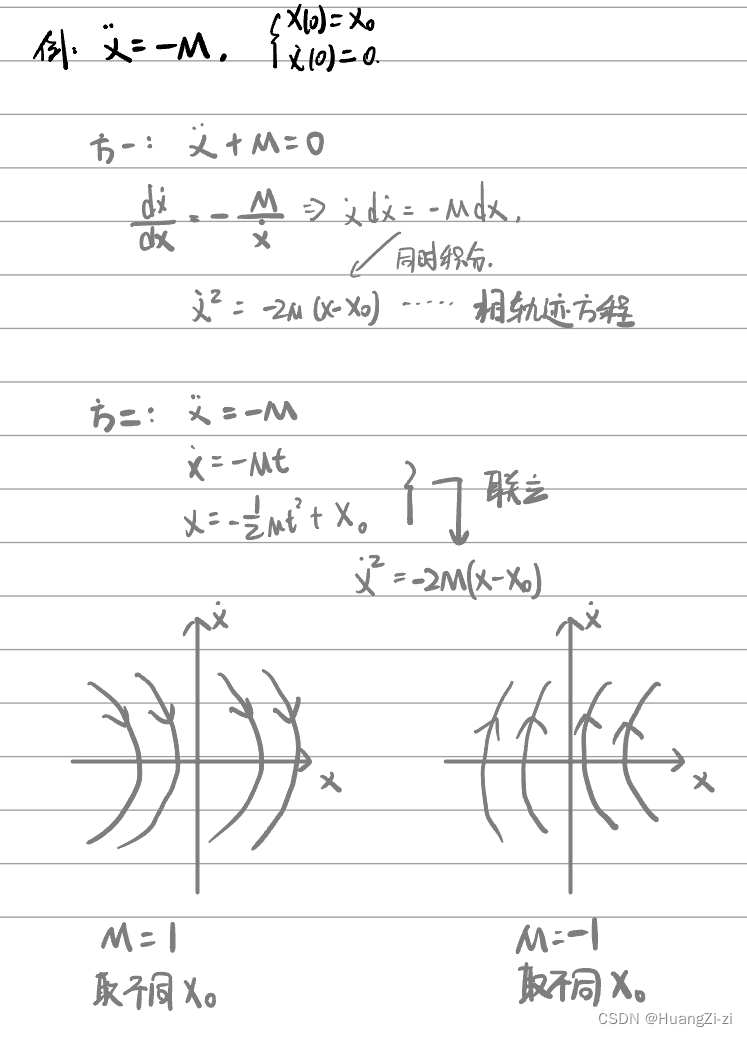
解析法
直接运算出相轨迹方程,然后将函数关系画出来。
大多数时候,相轨迹方程不好算,所以这个方法其实不太常用
等倾线法
线性系统的相平面分析
典型二阶系统:
Φ ( s ) = ω n 2 s 2 + 2 ξ ω n s + ω n 2 \Phi(s)=\displaystyle \frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2} Φ(s)=s2+2ξωns+ωn2ωn2
X ¨ + 2 ξ ω n X ˙ + ω n 2 X = 0 \ddot{X}+2\xi\omega_n\dot{X}+\omega_n^2X=0 X¨+2ξωnX˙+ωn2X=0
d X ˙ d X = − 2 ξ ω n + ω n 2 X X ˙ \displaystyle \frac{\rm{d}\dot{X}}{\rm{d}X}=-\frac{2\xi \omega_n+\omega_n^2X}{\dot{X}} dXdX˙=−X˙2ξωn+ωn2X
根据闭环极点不同,相轨迹不同:
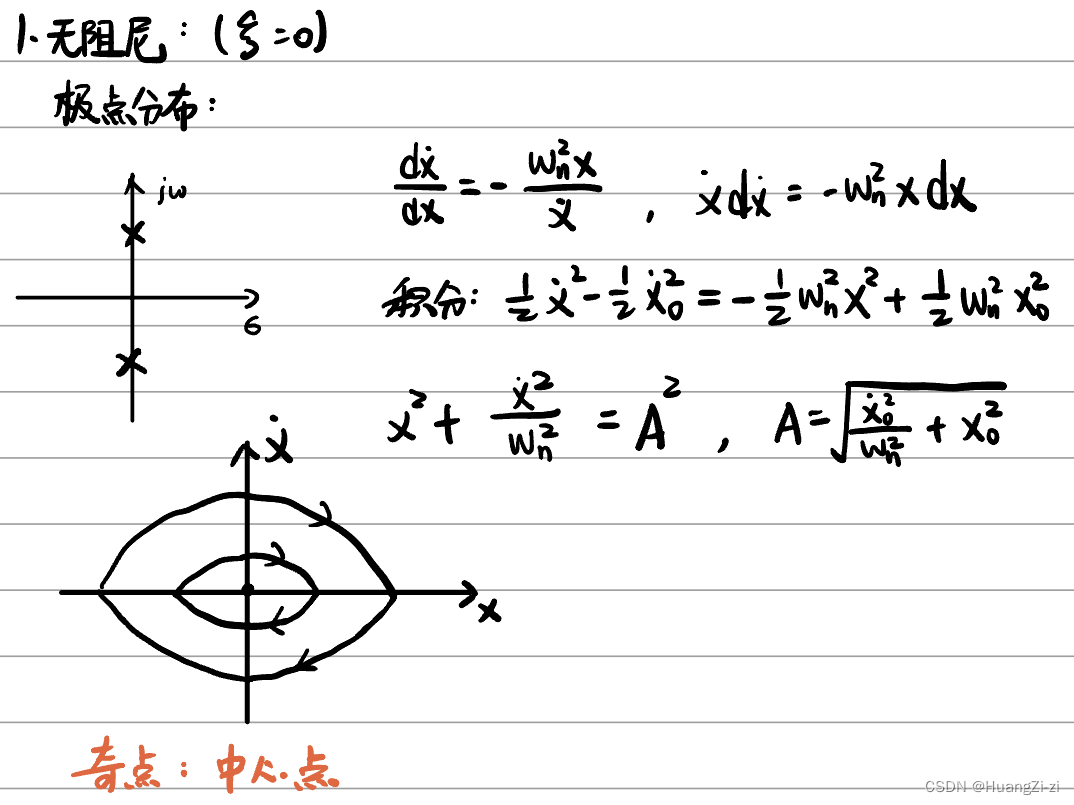
-
两个纯虚根
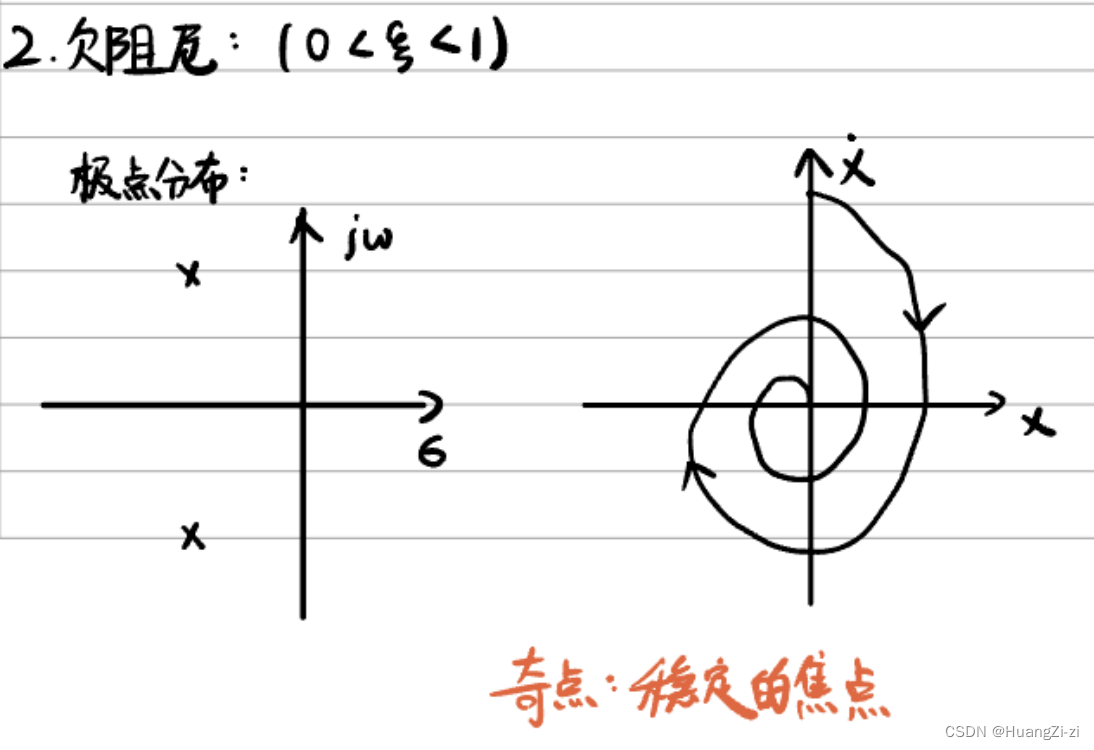
-
共轭复根(虚轴左侧)
-
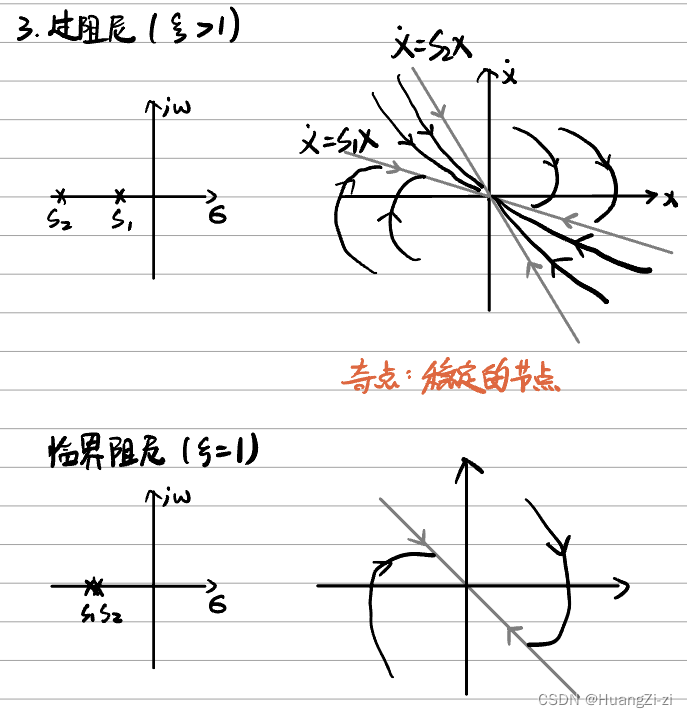
两个实根(虚轴左侧)
-
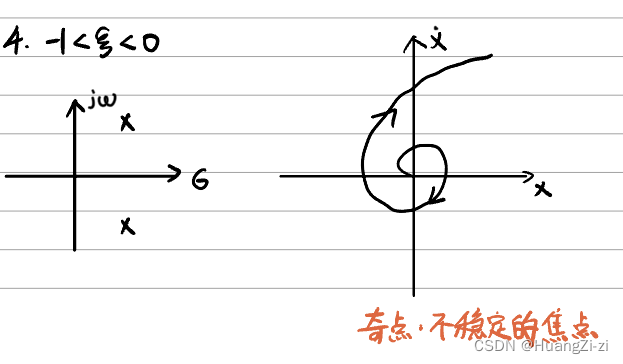
共轭复根(虚轴右侧)
-
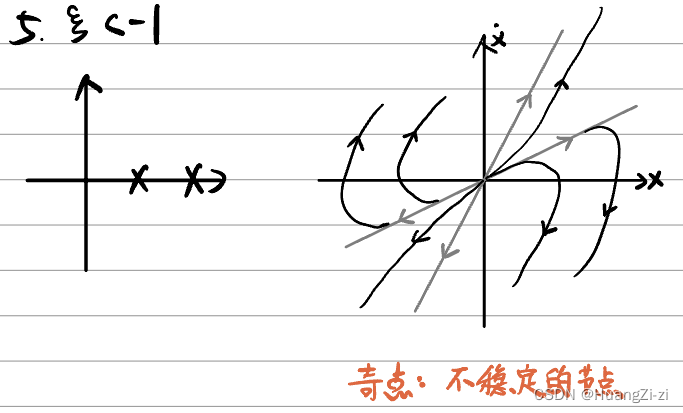
两个实根(虚轴右侧)
-
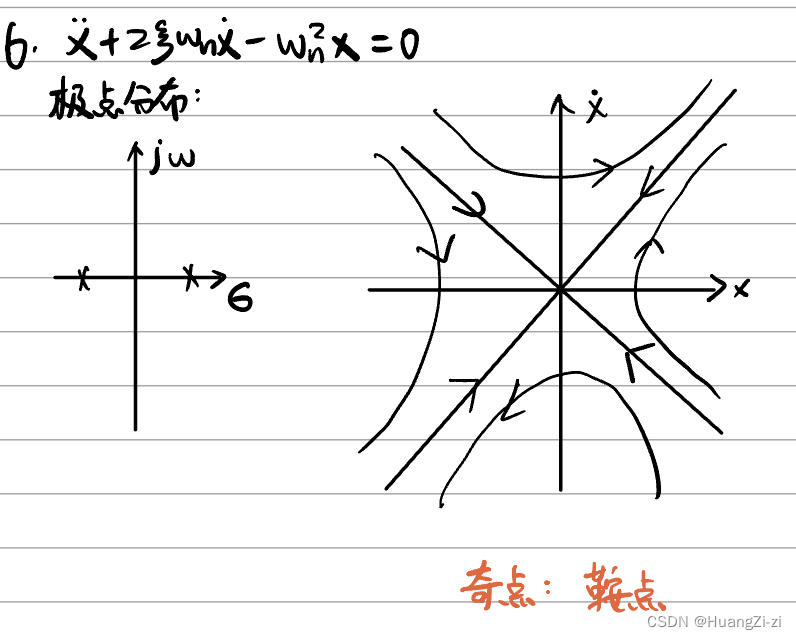
两个实根(一正一负)
非线性系统的相平面分析
这里涉及的非线性系统是非本质非线性系统,即连续的非线性系统。
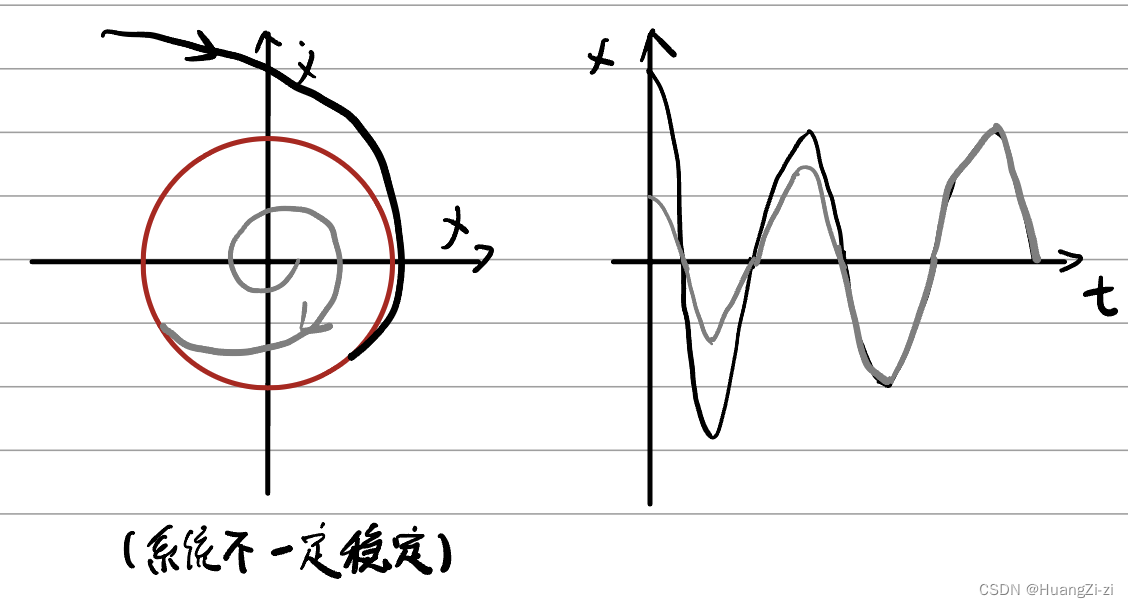
极限环等幅震荡
也就是之前提到的自激震荡现象。
-
稳定极限环:不论初始状态如何,相轨迹总收敛于极限环,系统趋于等幅震荡
-
半稳定极限环:相轨迹能否收敛,取决于初始值和受扰动情况
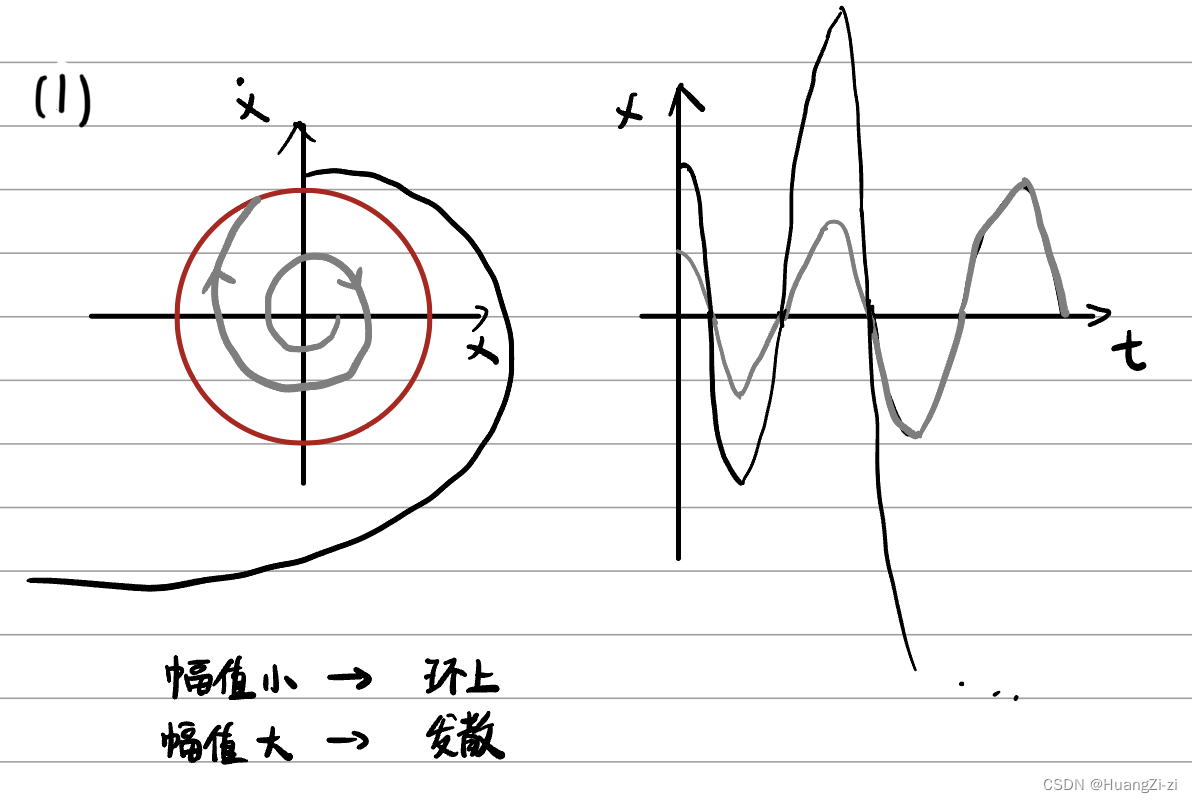
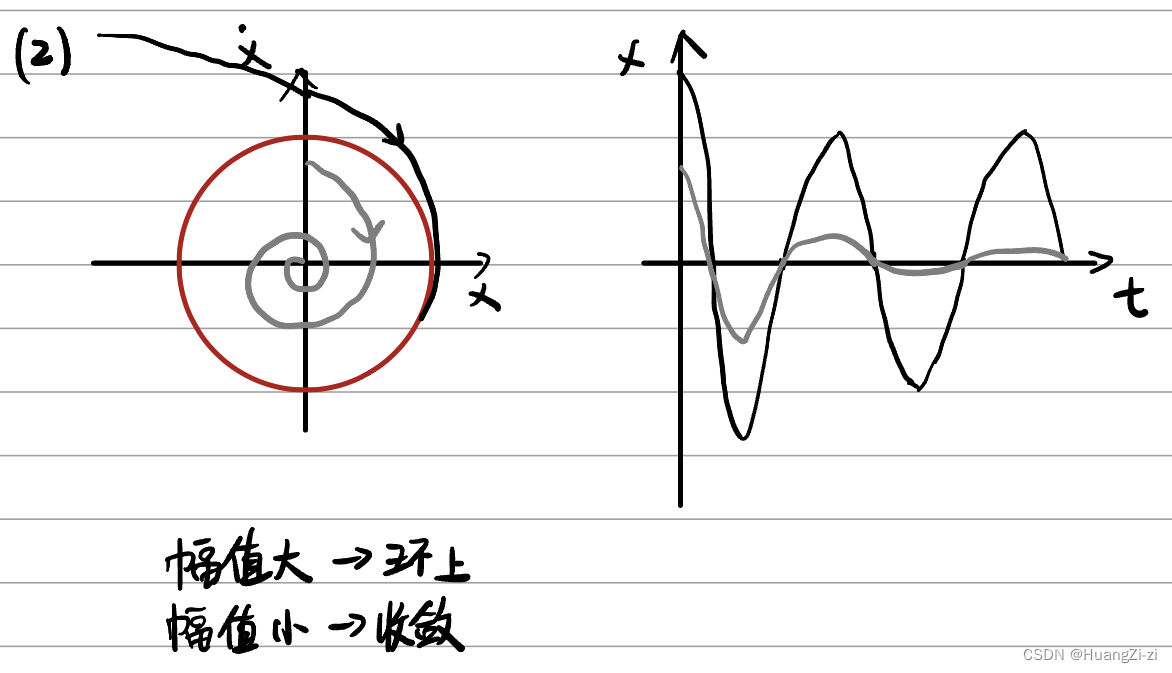
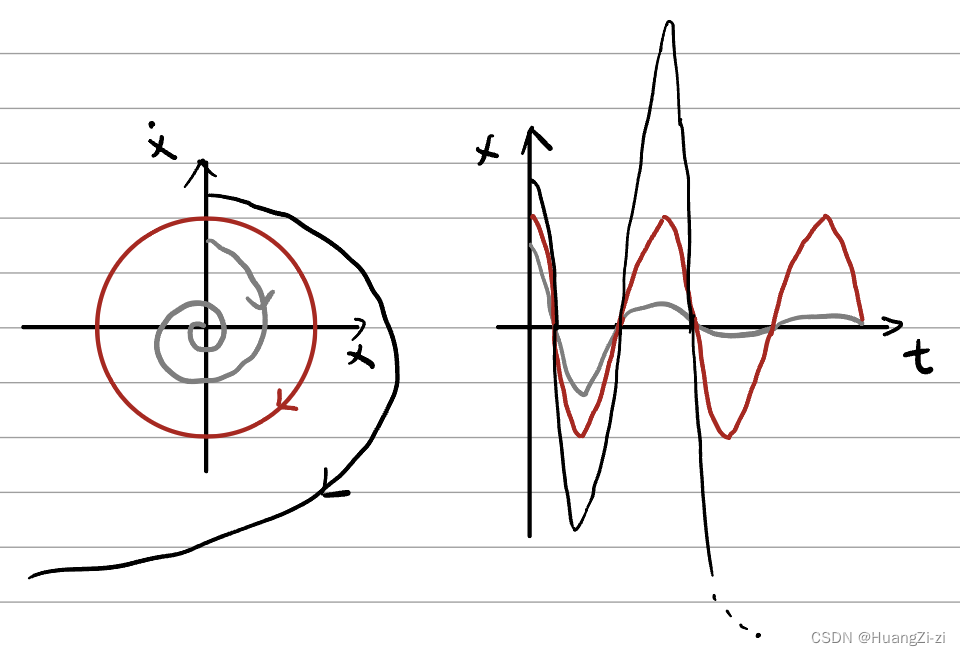
-
不稳定极限环:极限环内外,相轨迹或收敛于它,或由它发散而去
如果不稳定极限环内外没有其他的极限环,则它就是孤立极限环。
利用相平面法分析系统
- 找系统平衡点:让参变量各阶导数为0,求微分方程的解
- 绘制相轨迹,分析平衡点附近相轨迹性质。如上题,则有可能产生极限环,发生等幅震荡,也有可能平衡点处是稳定的节点。
- 一部分二阶非线性系统,求出平衡点后,在平衡点处线性化,借助二阶系统的相轨迹分析其特性。
- 本质非线性:即不连续。使用分区绘制的方法
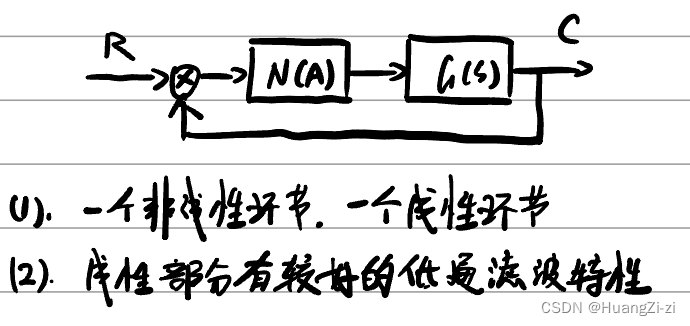
描述函数法
-
概述
一个周期函数,傅立叶展开:
如果这个周期函数是奇对称的,则 A 0 = 0 A_0=0 A0=0 (A0称为直流分量)
如果忽略高次谐波,认为只有基波分量有意义,则可以将非线性环节近似为线性环节,即谐波线性化。
定义描述函数:输出信号基波分量与输入信号的相量比(幅值相除,相角相减)
对于奇对称的非线性环节,描述函数仅与输入幅值A有关。(课程中涉及的典型非线性环节都是奇对称的) -
应用描述函数分析非线性系统的条件
典型非线性特性的描述函数
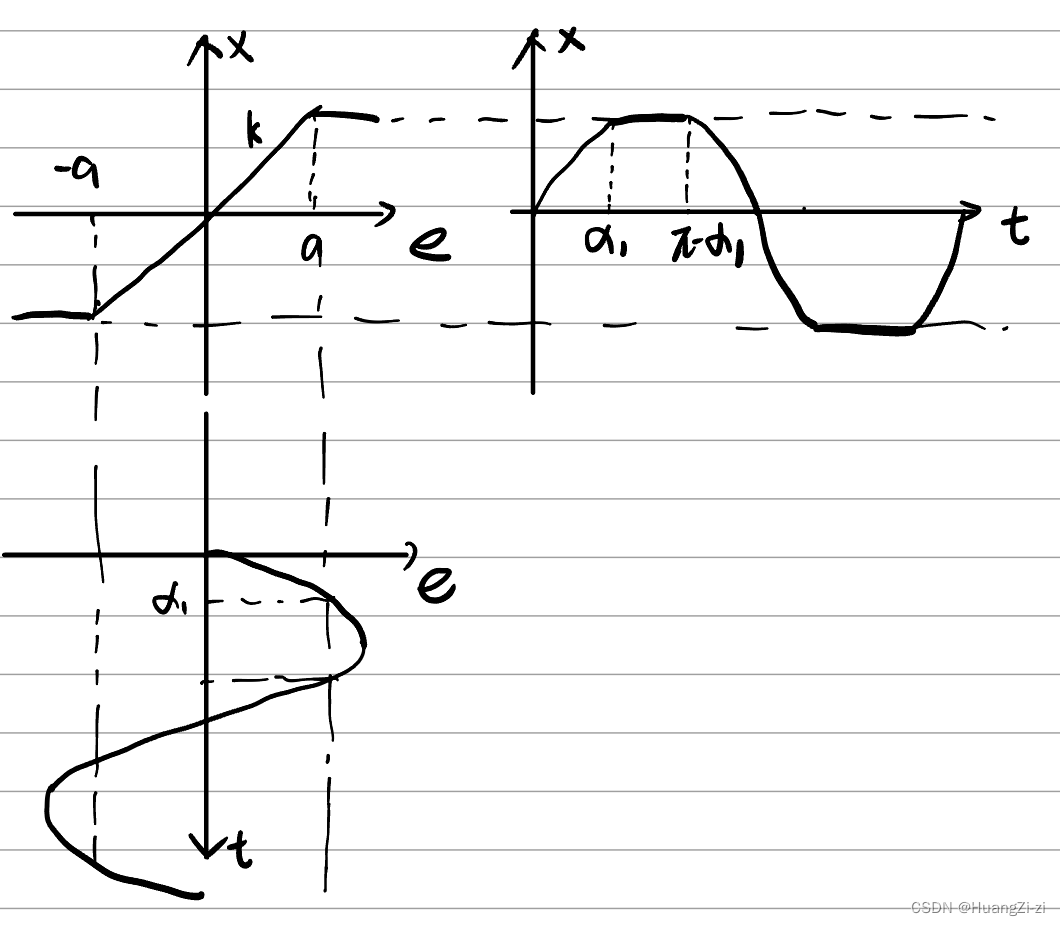
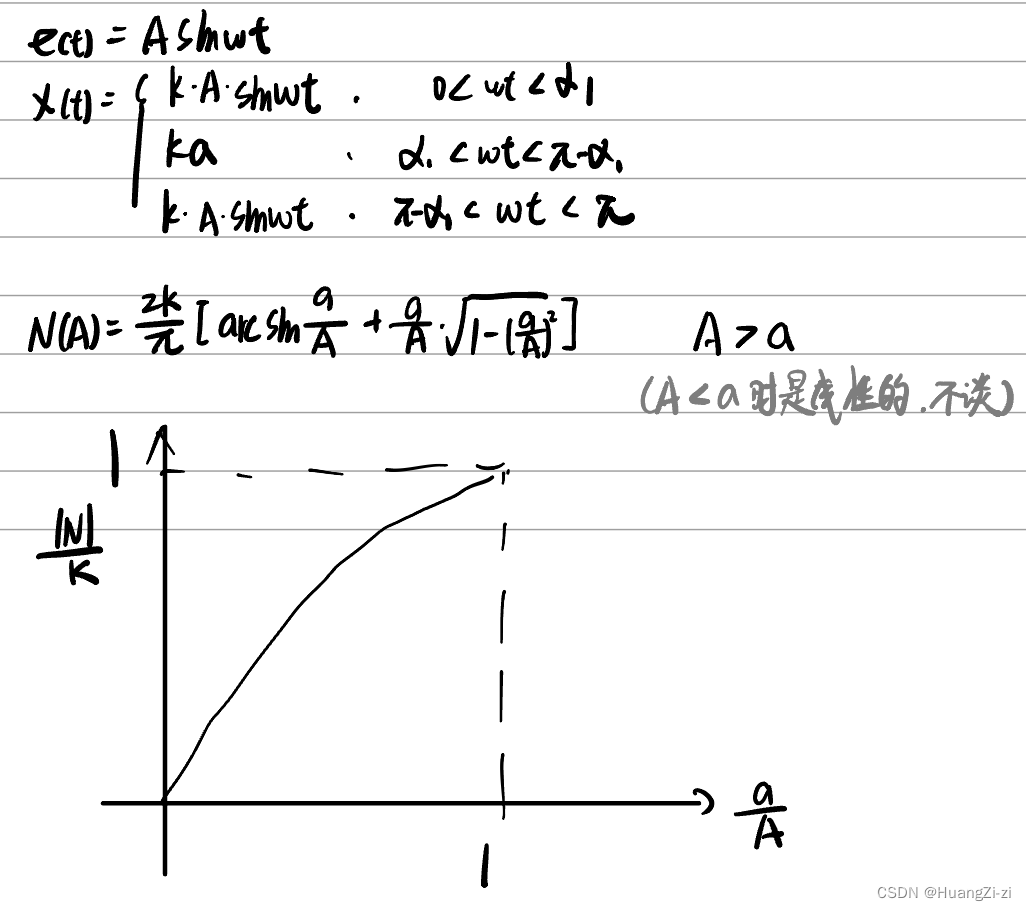
- 饱和特性
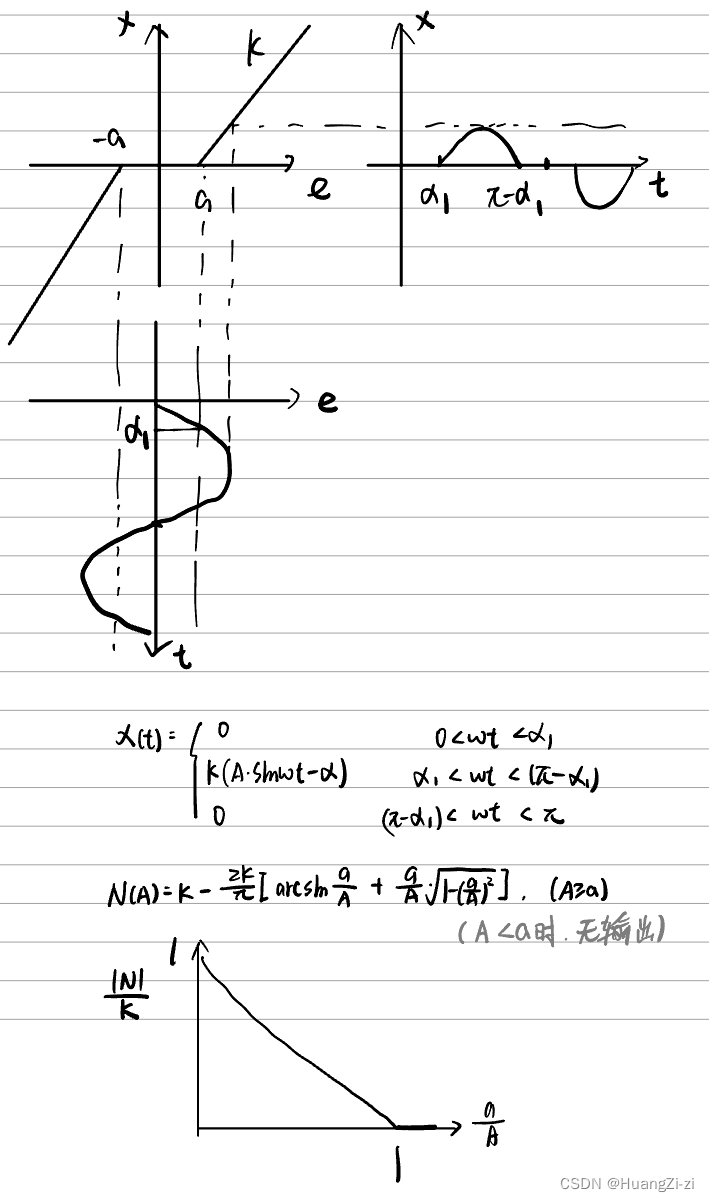
- 死区特性
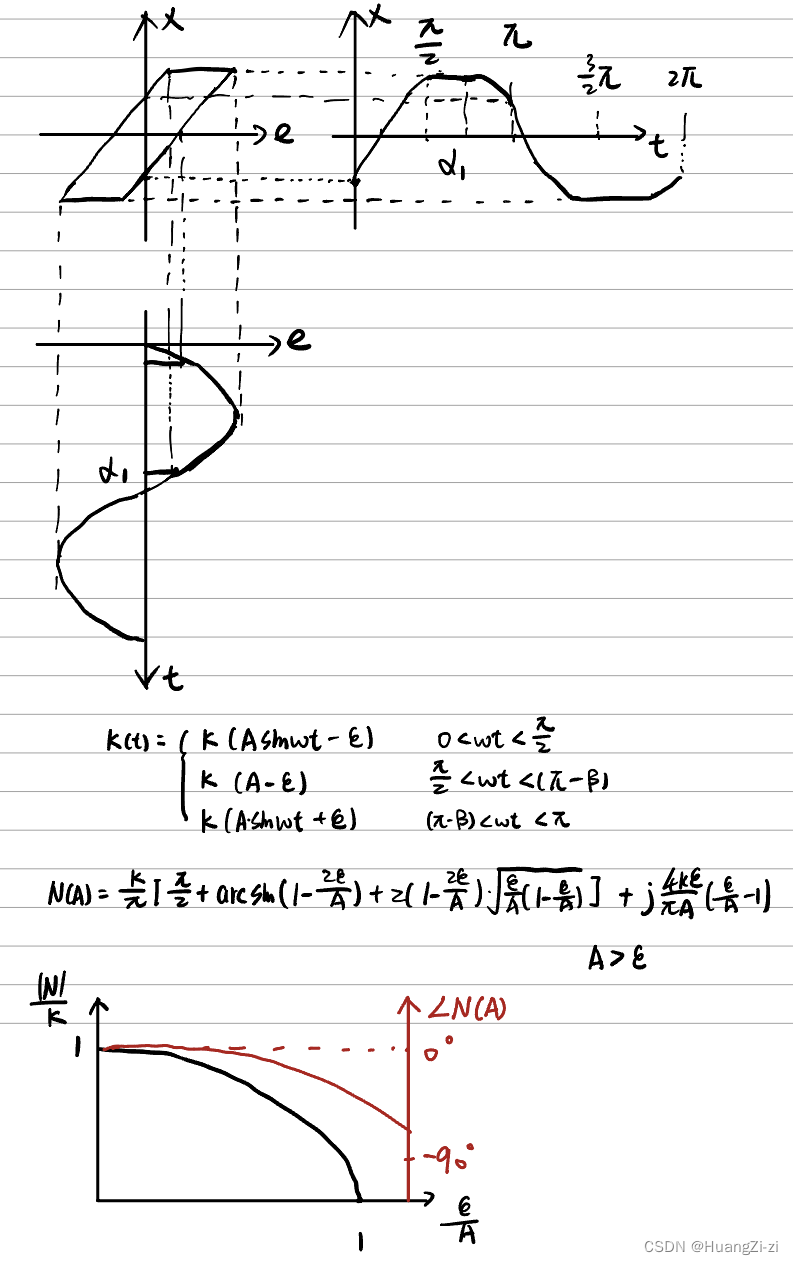
- 间隙特性
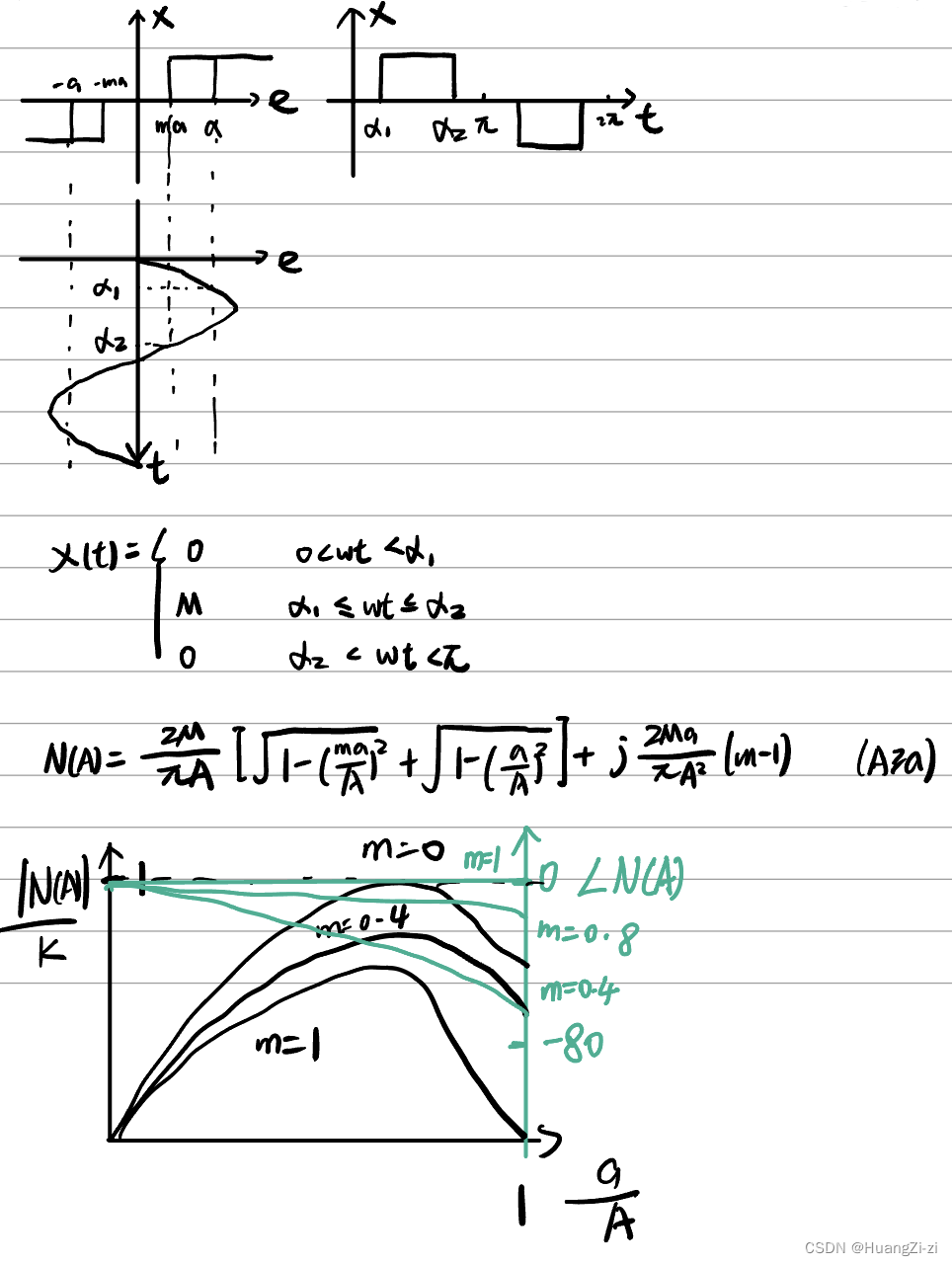
- 继电器特性
特殊情况:
利用描述函数法分析系统稳定性
原理
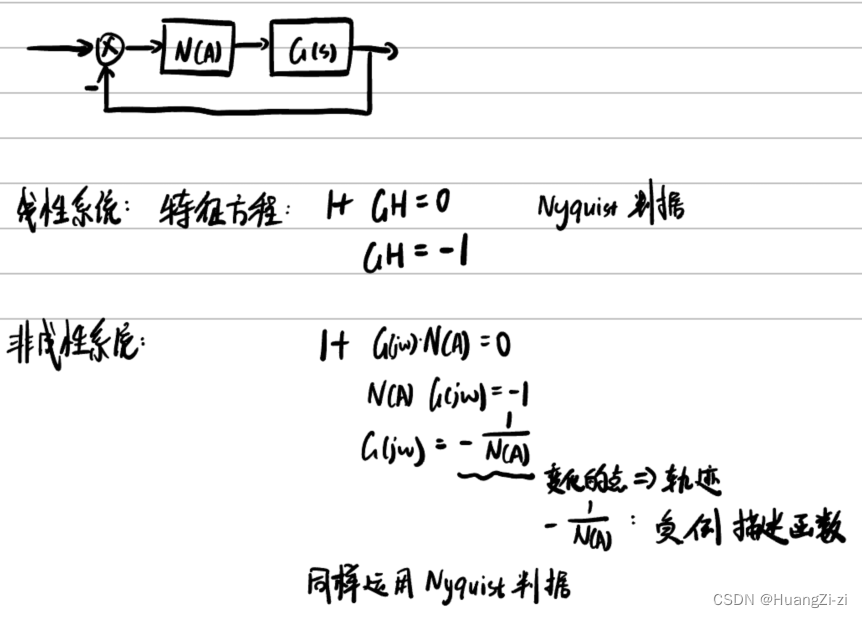
奈奎斯特稳定判据:特征方程化成GH=-1的形式,看幅相频率曲线包围(-1,j0)点的圈数分析稳定性。
将描述函数代入,特征方程化成NG=-1的形式,进而化为G=-1/N的形式,看幅相频率曲线包围负倒描述函数上某点的圈数,分析稳定性。
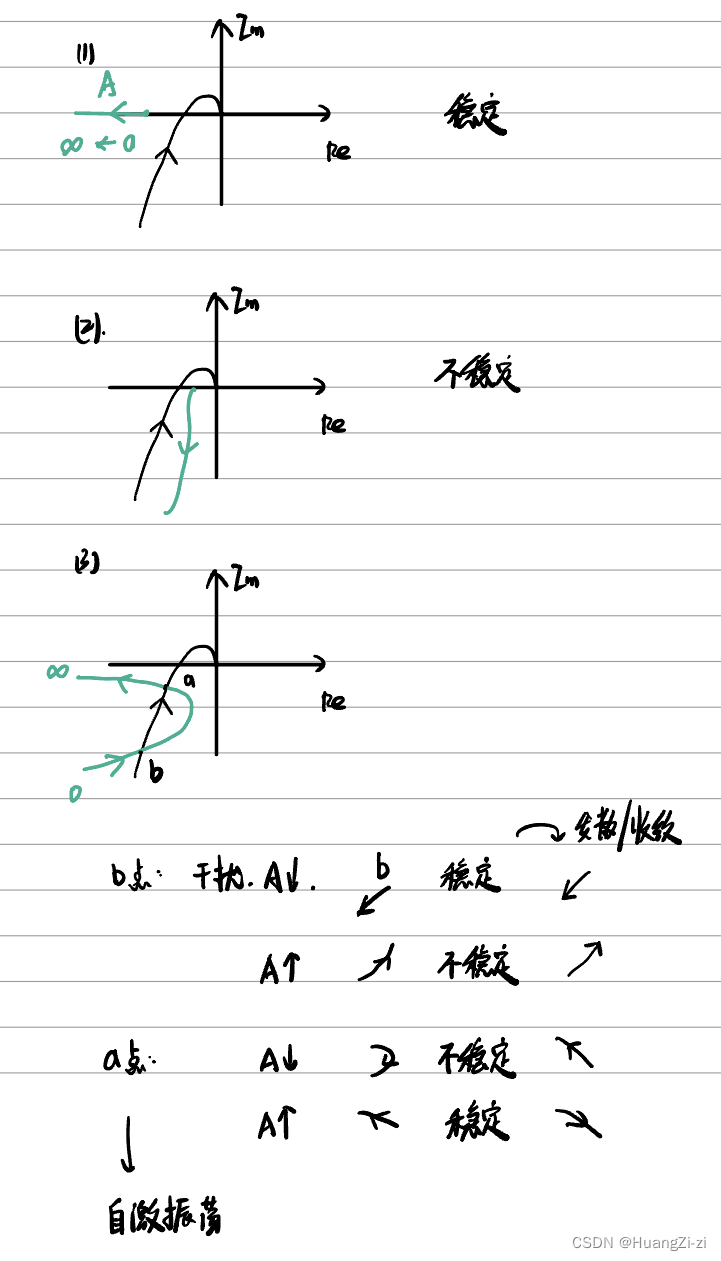
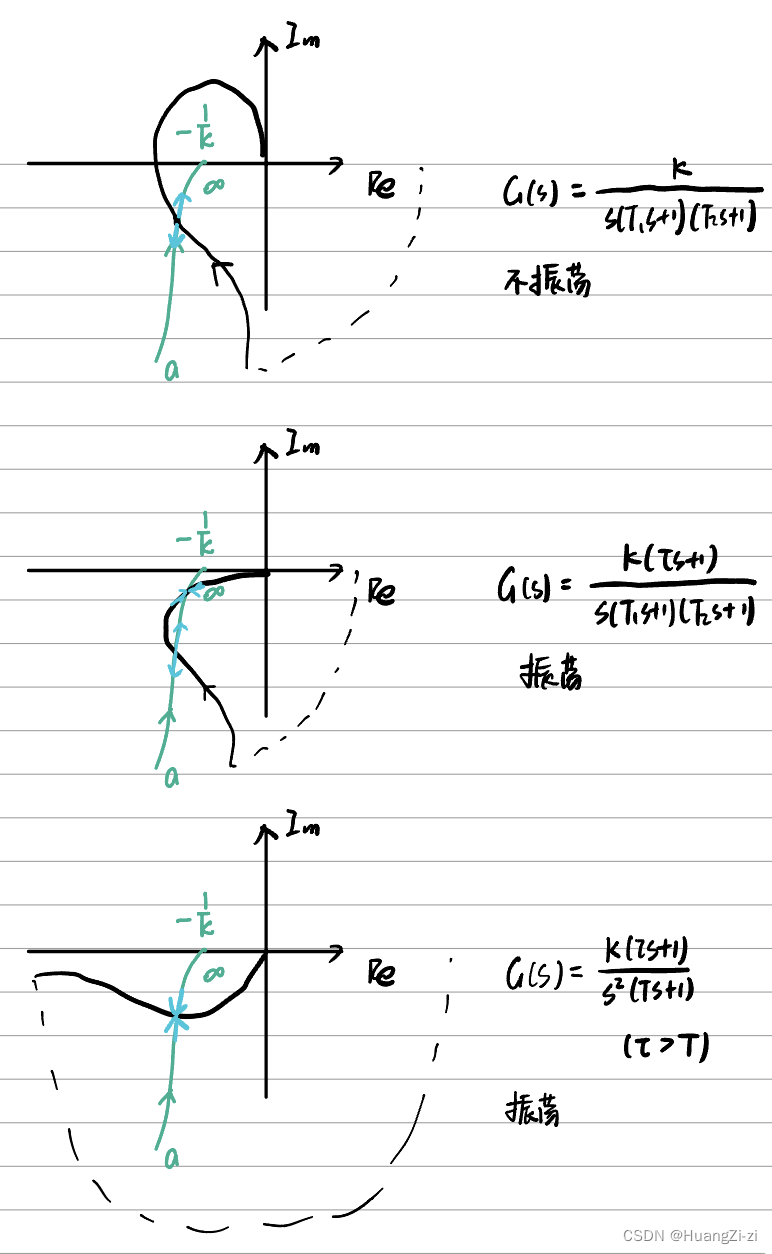
典型非线性特性对系统稳定性的影响
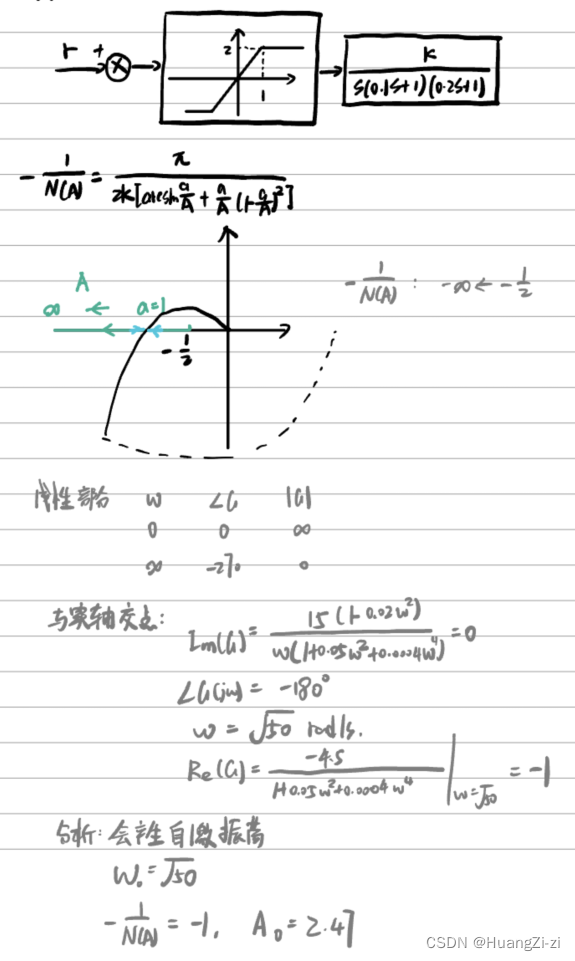
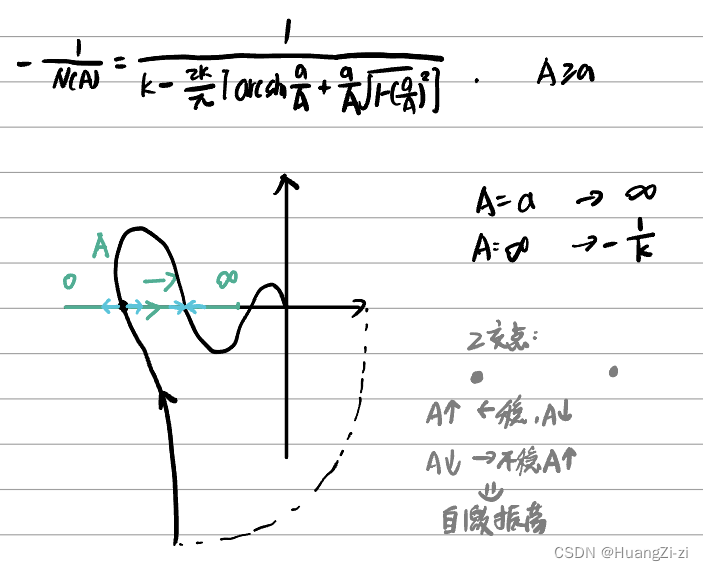
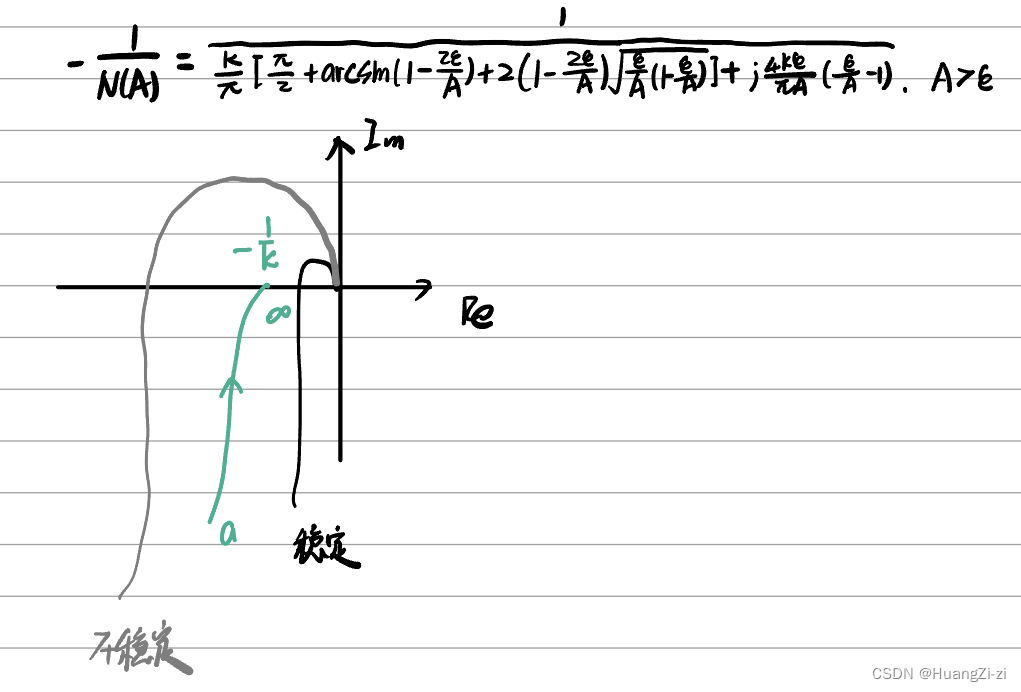
非线性特性对系统稳定性的影响主要还是跟两条曲线的位置关系有关,这里主要学习各典型非线性特性的负倒描述函数曲线的画法。「注意绿色曲线的形状和走向」
- 饱和特性
- 死区特性
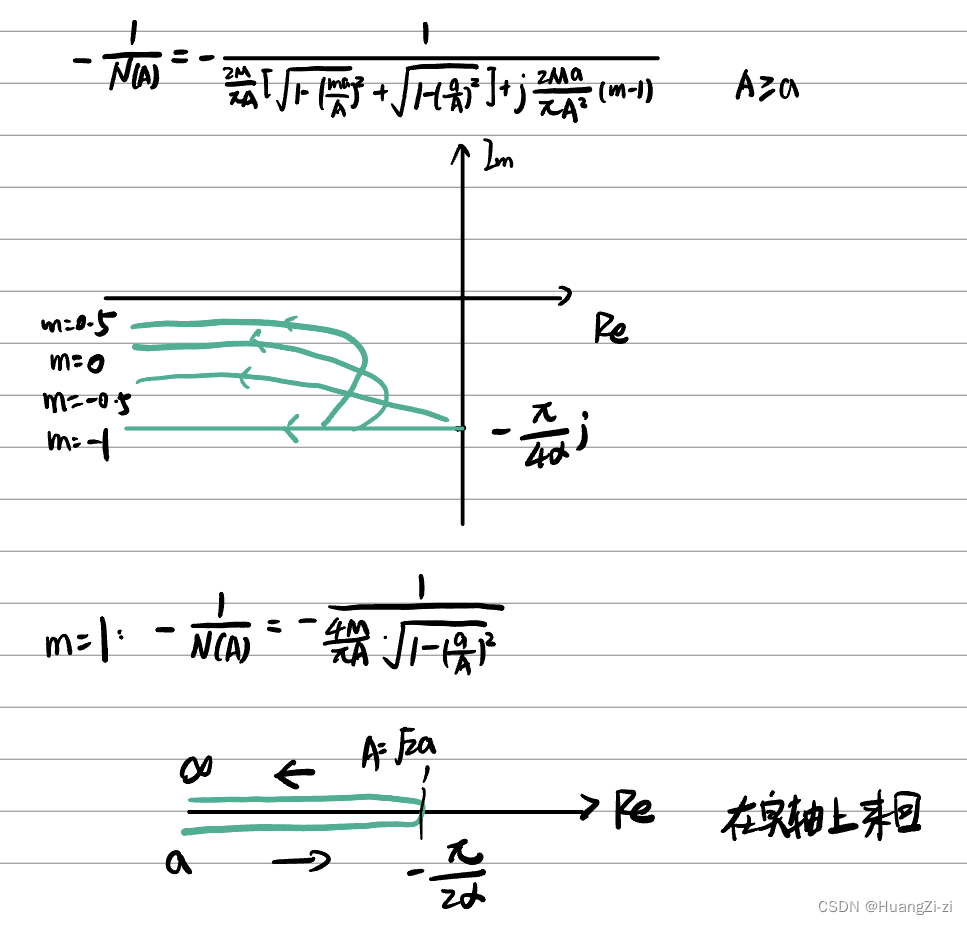
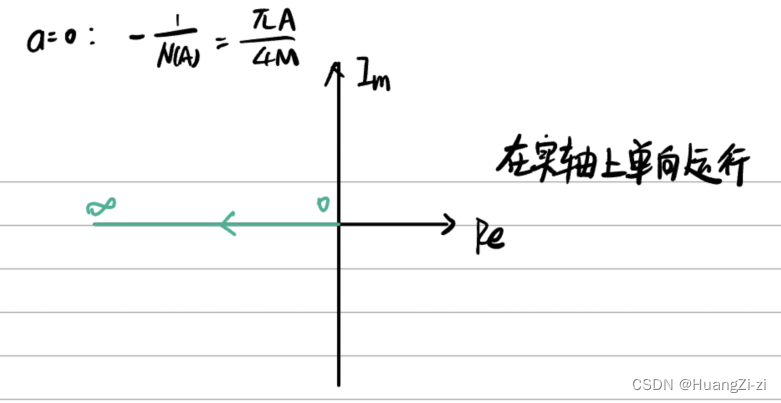
- 间隙特性
- 继电器特性
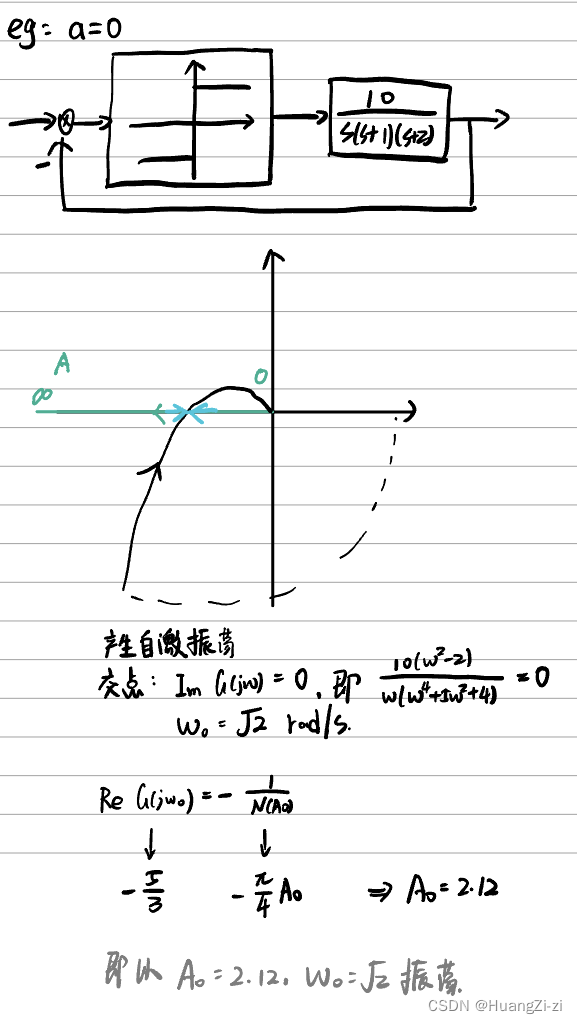
以上分析发现,非线性特性的加入,有可能使系统产生自激震荡,但这并不意味着系统一定会震荡。而是仅当系统输入达到某些条件,才会激发出震荡的状态。
今天的文章非线性系统控制理论_非线性系统线性化的方法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/82634.html