1.定义:光学分辨率是用来描述光学成像系统解析物体细节的能力。
2.分辨率限制——艾里斑:光穿过任何尺寸的孔径时都会产生衍射,由此产生的衍射图案称为艾里斑。
孔径:每个镜头都具有限定的孔径。成像系统的孔径限制包括镜片尺寸、光圈尺寸等。
衍射图案/艾里斑:中心是一块明亮区域,周围是一系列亮度不断降低的同心圆环。艾里斑是一个极小的点光源通过理想透镜后于像面所形成的,由于光的波动性,无法还原为极小的点。
注:根据惠更斯原理,波前上的每一个点都可以是作为独立的子球面波光源,所以无数个子波之间互相抵消或增强,形成新的波前。当波前受限于孔径时产生衍射效应,造成波前向后弯曲,在像面形成一个由中心亮斑和一组照度快速下降的同心圆环组成的斑点,这就是艾里斑。
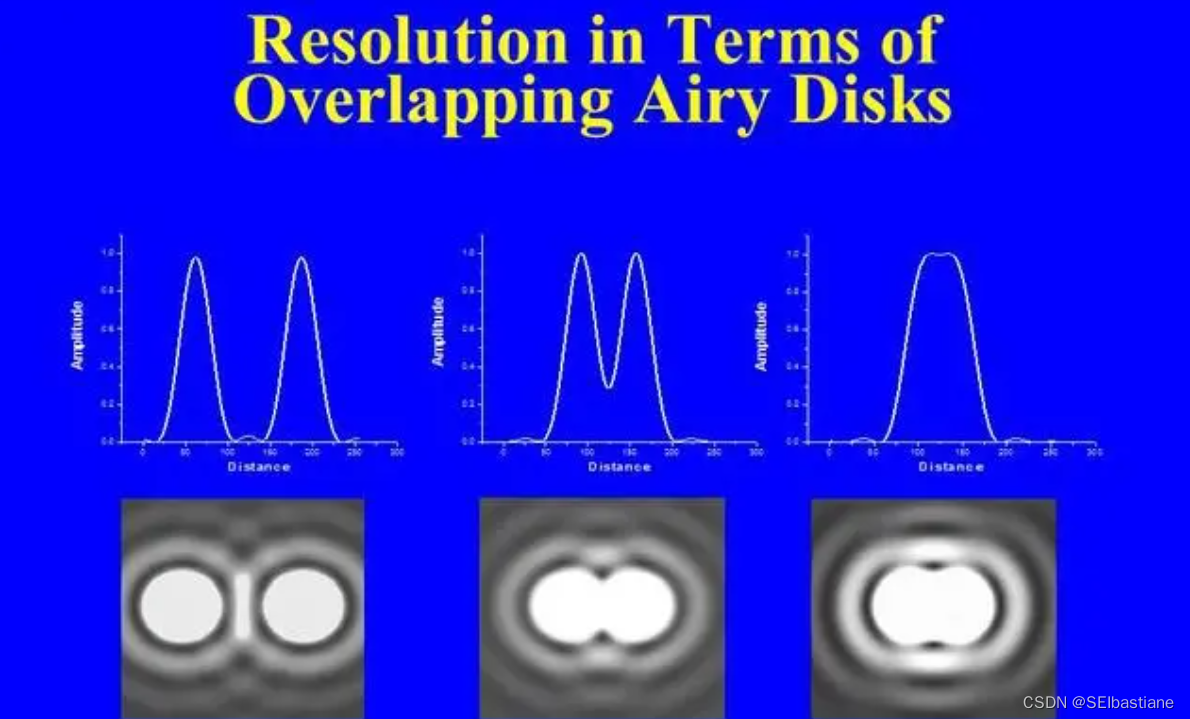
3.极限分辨率:由一个有限孔径的光学系统产生的艾里斑衍射图确定
①物体上的不同细节聚焦产生的艾里斑图案会紧密靠近
②开始重叠
③当重叠图案对降低对比度造成具有足够干扰时,最终无法相互区分:两个临近的艾里斑靠近,直至它们各自中心亮斑峰值的距离下降到
4.瑞利判据:当两个等强度且不相干的光狭缝亮纹互相靠近而快要重叠时,两者的光强度叠加之后,中心处亮暗纹的光强度比最亮处的光强度小一些,减小成为约 81% ,恰好可以判断出来是来自于两个不同的光狭缝。
①计算两个峰值距离z/像素间最小间距
当一个衍射斑的极大值和另一个衍射斑的第一条暗纹重合,之间就出现清晰的界限。根据瑞利判据,此时两个峰值的距离Z就等于:
若以像素对应,取
②计算最小分辨率开角θ
角分辨率是指成像系统或系统的一个部件的分辨能力,即成像系统或系统元件能有差别地区分开两相邻物体最小间距的能力,一个光学仪器的角分辨度(英文:angular resolution)指仪器能够分辨远处两件细小物件下,它们所形成的最小夹角。分辨本领一般用成像系统对两个最小可辨目标之间所张角度大小表示,通常用测度角的弧度系统描述,亦称角分辨本领(或角分辨率)。
从透镜的角度考虑角分辨率,此时对应的最小角分辨率函数为:
θ为最小角,D为出瞳系统孔径,减小波长(λ)或增大孔径都能提高极限分辨率。此图案的直径与照明光线的波长(λ)以及圆形孔径的尺寸相关。但这俩显然都是有严格的限定范围(尤其对民用成像系统来说),用弧度来计算上式更为直观:

系统孔径越大,最小分辨率开角就越小。若以像素对应,取

单位为弧秒,同样是理想值。如天文望远中的杜氏极限描述了等亮星间距离大于等于4.6/D时,两颗星星才能目视分辨。而对于分光仪等光学仪器来说,分辨率N就表示它最小可探测的波长差是仪器使用波长的1/N。
5.数字成像系统光圈和分辨率的关系
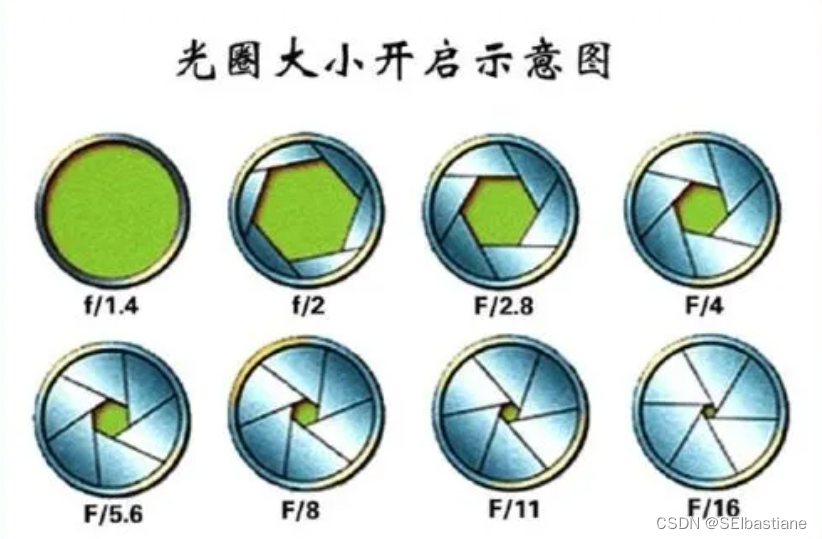
光圈系数F是用于表征光圈的大小的参数。f/#等于镜头焦距f和通光孔径D之比。光通量与F值的平方成反比关系,F值越小,光通量越大。F值后一个值正好是前一个数值的√2 倍,所以,光圈调大一挡,光量减少2倍。光圈常用值为1.4、2、2.8、4、5.6、8、11、16、22等几个等级。
数字成像系统里,使相邻艾里斑突破衍射极限的光圈F(f/#)是:
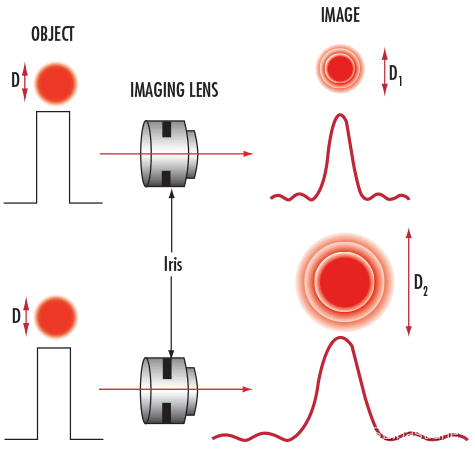
其中p为单个像素尺寸,所以在传感器尺寸一定的情况下,像素密度越高,极限衍射光圈越大。换言之,相同的像素总数,传感器尺寸越大,极限衍射光圈越小。随着像元尺寸的持续减小,F/#成为了限制系统成像质量的重要因素,因为它所影响景深和分辨率成反比的关系,景深增大,分辨率就降低。随着像素大小继续减小,其影响会越来越显著,最终难以克服。
图显示了最大光圈f/2.8的镜头组和f/8的镜头组之间的光斑大小差异。衍射随成像镜头光圈关闭而增加。
艾里斑(或最小光斑大小)可以使用f/#和波长(μm)计算:

表1显示了使用520nm绿光计算得出的不同f/#下的艾里斑直径。最小的可实现光斑大小可能会超过小像素的大小。导致获得具有对比度级别的传感器的完全分辨率能力时遇到困难。此外,这没有考虑任何镜头设计的局限性以及与镜头元件和光学组件相关的制造误差,而这些情况会导致生成物理可实现的最小光斑的能力降低,进而降低分辨率和对比度级别。
| f/# |
波长为520nm时的艾里斑直径 (μm) |
|---|---|
| 1.4 | 1.78 |
| 2 | 2.54 |
| 2.8 | 3.55 |
| 4 | 5.08 |
| 5.6 | 7.11 |
| 8 | 10.15 |
| 11 | 13.96 |
| 16 | 20.30 |
6.像差
注:艾里斑建立在理想的、无像差的、孔径具有均匀通过率的理想透镜,并有被均匀振幅的理想波前照射。像差和不均匀透射/波前振幅都会负面影响到分辨率,严格来说就是继续让原本就呈现艾里斑状扩散的像,继续以各种形态弥散开。
像差的类型非常多,按指数之和为级。
一级像差有2个:放大率和横向像差
三级像差有5个:球差、慧差、像散、场曲、畸变
五级像差有9个:五级球差、线性慧差、斜球差、椭球差等
七级像差14个
九级像差20个
n级像差:
实际都是像差的组合而非单项,其中比较熟悉的是三级像差了。
上图所示的各种球差看起来跟艾里斑很相似。是一个由光晕环绕的亮斑,无论过校正还是欠矫正,球差都会降低像的对比,使其细节模糊,所以一些镜头明明已经上焦但照片依然模糊,基本都是球差的问题。同时球差也是决定虚化效果的关键因素之一。
以此类推,色差会导致不同波长之间的互相干扰、慧差像散进一步扭曲像面的点扩散形式、暗角降低边缘信噪比……而且无论是多么完美的校正,像差也一定会存在,对分辨率的影响也自然一定存在,所以像素极限远不像理论那么高。
7.采样率
MTF这个词大家至少应该很眼熟,除了可以标定镜头分辨率之外,当然也可以衡量传感器的分辨率,而它们对应的都是空间频率,单位有线对/毫米(lp/mm)、线宽/像高(LW/PH)、线对/像高(lp/PH)、周期/像素(Cycles/Pixel)等等,听起来很不一样,但只是量度方式不同而已。
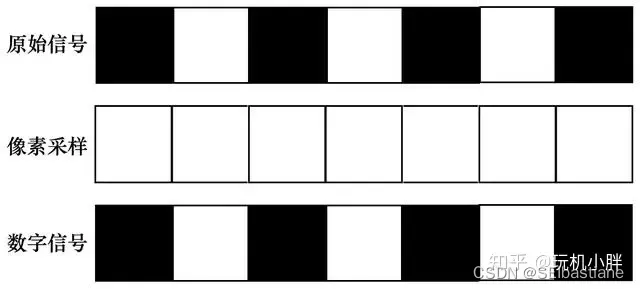
分辨率落实到具体意义上,就是看像面可以还原多少物面的细节,比如1000个线对拍出来之后还能分辨多少,如果是以黑白相间的正弦波为例:
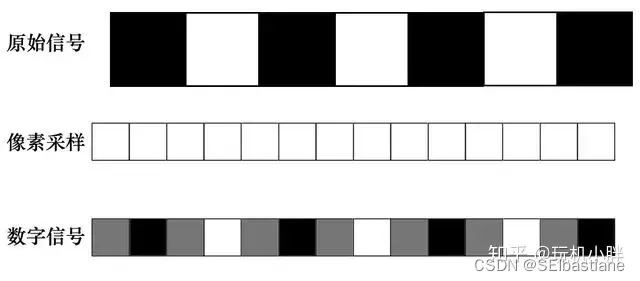
波峰与波谷分别对应1个像素,在一一对应的情况下,物面的1000个正弦波相位就需要1000个像面的对应点即可还原,在数字传感器上,像面的对应点也就是像素,像素密度就决定了采样率。
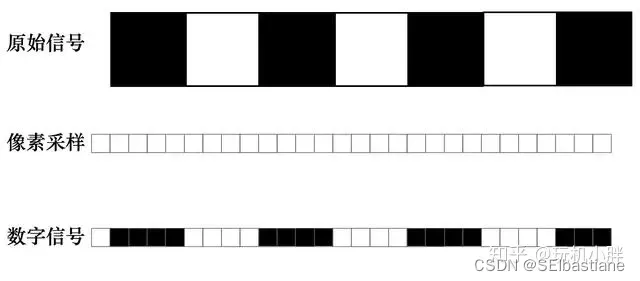
但即便是最简单的正弦波,它与像素/采样点也会存在相位差,如果是1:1采样,原始信号稍有一点相位差,像素就基本无法正确采样出物面的应有形状,出现摩尔纹或伪色,分辨率急剧下降:
这时候只能通过增加像素密度,也就是增加采样率来实现,而这就是奈奎斯特采样定律的意义所在了——在模拟信号与数字信号转换时,采样频率需大于模拟信号最高频率2倍,才能保证数字信号完整保留原始信息,传感器的奈奎斯特频率有公式:(z像素间距)
对于尺寸一定的传感器而言,像素间距越小,也即像素密度越大,奈奎斯特频率越高,这也是为什么说“像素即正义”的原因,依然是一个简单的正弦波,高采样率在各种相位差的影响下也能更好地还原信号,提升可以容忍频率更高的正弦波并还原,换句话说就是提高了分辨率:
可以看到2倍还不算特别靠谱,实际应用中甚至要求奈奎斯特频率是模拟信号峰值频率的5-10倍,也即1个极小点光源需要5-10个像素来采样还原:
这样是不是好多了?用我们一开始拍细菌的案例来说,8.64亿个1微米直径的细菌,需要43.2-86.4亿像素去进行采样。而按照衍射极限理论,550nm单光照射时,至少需要一块51mm X 34mm的传感器才能踩到理论门槛,而且依然是在无视现有数字传感器工艺和透镜系统像差的极理想条件下。
简像素密度高采样率高,利于消除摩尔纹、伪色,并提高锐度。
突破分辨率极限的手段——拼接
前面讨论的分辨率极限基于单次拍摄。事实上也受制于传感器尺寸,因为不能无限扩大传感器尺寸。现在的极高分辨率摄影几乎都选择了相同的方法突破分辨率极限——拼接。
这是260张D850+300mm F2.8拍摄的照片拼接而成,总像素达到73亿!如果是每一张都贴边拍摄的话,总像素应该是117亿,但全景都需要边缘重叠,所以减去重叠部分,这张照片相当于使用了140400mm^2的传感器,按3:2比例计算(虽然照片并不是这个比例),也即459mm X 305mm的传感器进行拍摄。这个尺寸是什么概念?8X10英寸大画幅页片的尺寸是201.7mm X 252.5mm……当然,这只是简单计算,并不严谨(比如每一张的曝光时间可能并不一致,相当于做CMOS HDR了)。而这张截图只展示了它155度视角里的一小部分而已,这么多照片的拼接意味着一件事:你可以进行相当任性的局部放大,比如这样:
是的,就是前一张图中部偏上的那个塔尖,拼接超高分辨率照片可以说是效果惊人,但过程也无比繁琐甚至昂贵,还伴随着很高的失败率,但在追求极限的路上摄影师们也从未掉队。对于普通摄影爱好者来说只需要理解一件事——在不考虑图像处理器主观性的前提下,现有传感器的分辨率远未到极限,别忘了在信噪比的章节我们还提过高像素缩图大法的优点,因此未来三五年看到主流机型突破半亿甚至逼近1亿像素,同时连拍对焦还刷得飞起,我觉得都是无需意外的事情,因为它本就应该会发生……
今天的文章光学分辨率越高越好吗_正确对比度分辨率的概念是「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83823.html