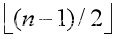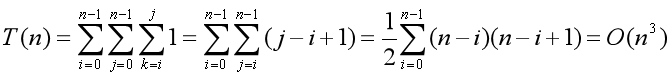一、问题描述
给定有n(n ≥ 1)个整数的序列,求出其中最大连续子序列的和。
例如:序列{-2, 11, -4, 13, -5, -2}的最大连续子序列和为20
序列{-6, 2, 4, -7, 5, 3, 2, -1, 6, -9, 10, -2}的最大连续子序列和为16
规定:一个序列的最大连续子序列和至少是0,如果小于0,其结果为0
二、问题求解(三种方法)
1. 分治法
算法思路:
对于含有n个整数的序列a[0…n – 1]:
-
若n=1,表示该序列仅含一个元素,若该元素大于0,则返回该元素,否则返回0
-
若n>1,先求出该序列的中间位置mid=
,该序列的最大连续子序列和所在的子序列只可能位于三个位置:
(1)该子序列完全位于序列的左半部,即a[0…mid]中。采用递归的方法求出其最大连续子序列和,命名为:max_left_sum。(2)该子序列完全位于序列的右半部,即a[mid + 1…n – 1]中。采用递归的方法求出其最大连续子序列和,命名为:max_right_sum。
(3)该子序列跨越中部而占据左右两部分,即a[mid]被包含在该子序列中。求出左半部从a[mid]开始的最大连续子序列和,命名为:max_left_boarder_sum =
{0 ≤ i ≤ mid}
;再求出右半部从a[mid + 1]开始的最大连续子序列和,命名为:max_right_boarder_sum =
{mid + 1 ≤ j ≤ n – 1}
。这种情况下序列的最大连续子序列和为:max_left_boarder_sum + max_right_boarder_sum,命名为:max_mid_sum。
求出三种情况中的最大值(即max_left_sum, max_right_sum, max_mid_sum中的最大值),即为所求。
代码展示:
#include <iostream>
using namespace std;
int max3(int num1, int num2, int num3) {
if (num1 > num2) {
num2 = num1;
}
return num2 > num3 ? num2 : num3;
}
int max_sub_sum(int a[], int str, int end) {
if (str == end) {
if (a[str] < 0) {
return 0;
}
else {
return a[str];
}
}
else {
int max_left_sum, max_right_sum;
int mid = (str + end) / 2;
max_left_sum = max_sub_sum(a, str, mid);
max_right_sum = max_sub_sum(a, mid + 1, end);
int max_left_boarder_sum = 0, max_right_boarder_sum = 0;
int left_boarder_sum = 0, right_boarder_sum = 0;
for (int i = mid; i >= str; i--) {
left_boarder_sum += a[i];
if (left_boarder_sum > max_left_boarder_sum) {
max_left_boarder_sum = left_boarder_sum;
}
}
for (int i = mid + 1; i <= end; i++) {
right_boarder_sum += a[i];
if (right_boarder_sum > max_right_boarder_sum) {
max_right_boarder_sum = right_boarder_sum;
}
}
int max_mid_sum = max_left_boarder_sum + max_right_boarder_sum;
return max3(max_left_sum, max_mid_sum, max_right_sum);
}
}
int main() {
int a[] = {
-2, 11, -4, 13, -5 ,-2 };
int len = sizeof(a) / sizeof(a[0]);
int value = max_sub_sum(a, 0, len - 1);
cout << "最大连续子序列和为:" << value << endl;
return 0;
}
算法分析:
设求解序列a[0…n – 1]最大连续子序列和的执行时间为T(n)。
- 若n = 1,则T(n) = 1。
- 若n > 1,则T(n) = 2 * T(n / 2) + O(n)
根据主定理,该算法时间复杂度为O(n*logn)
2. 蛮力法
蛮力法一共包括三种解法:
解法1:
算法思路:
设含有n个整数的序列a[0…n – 1]和其中任何连续子序列a[i…j](i ≤ j,0 ≤ i ≤ n – 1,i ≤ j ≤ n – 1),求出它的所有元素之和this_sum,并通过比较将最大值存放在max_sum中,最后返回max_sum。
例如:对于a[0…5] = {-2, 11, -4, 13, -5, -2},求出的a[i…j](i ≤ j)的所有元素和如图所示,其中20是最大值,即最大连续子序列和。
代码展示:
#include <iostream>
using namespace std;
#define INF 9999
int max_sub_sum(int a[], int len) {
int this_sum = -INF, max_sum = -INF;
for (int i = 0; i <= len - 1; i++) {
for (int j = i; j <= len - 1; j++) {
this_sum = 0;
for (int k = i; k <= j; k++) {
this_sum += a[k];
}
if (this_sum > max_sum) {
max_sum = this_sum;
}
}
}
return max_sum;
}
int main() {
int a[] = {
-2, 11, -4, 13, -5 ,-2 };
int len = sizeof(a) / sizeof(a[0]);
int value = max_sub_sum(a, len);
cout << "最大连续子序列和为:" << value << endl;
return 0;
}
算法分析:
因为算法中使用了三重循环,所以有:
解法2:
算法思路:
改进前面的算法,在求两个相邻子序列之和时他们之间相互关联。例如:设Sum(a[i…j])表示a[i…j]中所有元素的和。Sum(a[0…3]) = a[0] + a[1] + a[2] + a[3],而Sum(a[0…4]) = a[0] + a[1] + a[2] + a[3] + a[4],在前者计算出来的情况下求后者只需要在前者的基础上加上a[4]即可,没有必要每次都重复计算,即求Sum(a[i…j])时的递推关系如下:
代码展示:
#include <iostream>
using namespace std;
#define INF 9999
int max_sub_sum(int a[], int len) {
int this_sum = -INF, max_sum = -INF;
for (int i = 0; i <= len - 1; i++) {
this_sum = 0;
for (int j = i; j <= len - 1; j++) {
this_sum += a[j];
if (this_sum > max_sum){
max_sum = this_sum;
}
}
}
return max_sum;
}
int main() {
int a[] = {
-2, 11, -4, 13, -5 ,-2 };
int len = sizeof(a) / sizeof(a[0]);
int value = max_sub_sum(a, len);
cout << "最大连续子序列和为:" << value << endl;
return 0;
}
算法分析:
由于算法仅使用了两层循环,时间复杂度如下:
T(n) = O(n^2)
解法3:
算法思路:
进一步改进解法2,从头开始扫描数组a,用this_sum记录当前子序列之和,用max_sum记录最大连续子序列和。若在扫描中遇到负数,当前子序列和this_sum将会减小。若this_sum为负数,则可以放弃该子序列,重新开始下一个子序列的分析,并置this_sum = 0。若this_sum不断增加,则max_sum也不断增加。
代码展示:
#include <iostream>
using namespace std;
#define INF 9999
int max_sub_sum(int a[], int len) {
int this_sum = 0, max_sum = -INF;
for (int i = 0; i <= len - 1; i++) {
this_sum += a[i];
if (this_sum < 0) {
this_sum = 0;
}
if (this_sum > max_sum) {
max_sum = this_sum;
}
}
return max_sum;
}
int main() {
int a[] = {
-2, 11, -4, 13, -5 ,-2 };
int len = sizeof(a) / sizeof(a[0]);
int value = max_sub_sum(a, len);
cout << "最大连续子序列和为:" << value << endl;
return 0;
}
算法分析:
由于算法仅使用了一层循环,时间复杂度如下:
T(n) = O(n)
3. 动态规划法
算法思路:
对于含有n个整数的序列a[0…n – 1],设bj(1 ≤ j ≤ n)表示a[0…j – 1]的前j个元素中包含a[j – 1]的最大连续子序列和,bj-1表示a[0…j – 2]的前j-1个元素中包含a[j – 2]的最大连续子序列和。
显然,当bj-1 > 0时,bj = bj-1 + a[j – 1];当bj-1 ≤ 0时,放弃前面选取的元素,从a[j – 1]重新开始选取,bj = a[j ]。用一维动态规划数组dp存放b,对应的状态转移方程如下:
dp[0] = 0;
dp[j] = MAX{dp[j – 1] + a[j – 1], a[j – 1]} 1 ≤ j ≤ n
则序列a的最大连续子序列和等于dp[j](1 ≤ j ≤ n)中的最大者。
从中看到,若序列a的最大连续子序列和等于dp[maxj],在dp中从该位置向前找,值小于或等于0的元素dp[k],则a序列中从k + 1开始到maxj位置的所有元素恰好构成最大连续子序列。
例如:a序列为{-2, 11, -4, 13, -5, -2},dp[0] = 0,求其他元素如下:
其中,dp[4] = 20为最大值,向前找到dp[1] ≤ 0,所以由a2 ~ a4的元素即(11, -4, 13)构成最大连续子序列,和为20
代码展示:
#include <iostream>
using namespace std;
#define MAXN 20
int dp[MAXN];
void max_sub_sum(int a[], int len) {
dp[0] = 0;
for (int i = 1; i <= len; i++) {
dp[i] = max(dp[i - 1] + a[i - 1], a[i - 1]);
}
}
void show_result(int a[], int len) {
int maxi = 0;
for (int i = 1; i <= len; i++) {
if (dp[i] > dp[maxi]) {
maxi = i;
}
}
int str;
for (str = maxi; str >= 0; str--) {
if (dp[str] < 0) {
break;
}
}
cout << "求解结果" << endl;
cout << "\t最大连续子序列和:" << dp[maxi] << endl;
cout << "\t最大连续子序列:";
for (int i = str + 1; i <= maxi; i++) {
cout << a[i - 1] << " ";
}
cout << endl;
}
int main() {
int a[] = {
-2, 11, -4, 13, -5, -2 };
int len = sizeof(a) / sizeof(a[0]);
max_sub_sum(a, len);
show_result(a, len);
return 0;
}
算法分析:
由于算法仅包含一重循环,时间复杂度为:T(n) = O(n)
今天的文章递归的时间复杂度_解决最大子序列和问题的算法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:http://bianchenghao.cn/83847.html