圆周运动的 运 动 方 程 \blue{运动方程} 运动方程和 轨 迹 方 程 \blue{轨迹方程} 轨迹方程
1、圆周运动方程的 分 量 式 \red{分量式} 分量式
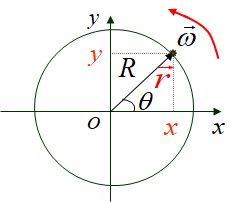
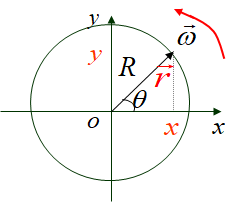
x = R c o s ( w t ) , y = R s i n ( w t ) , z = 0 x=Rcos(wt),y=Rsin(wt),z=0 x=Rcos(wt),y=Rsin(wt),z=0
1、圆周运动方程的 矢 量 式 \red{矢量式} 矢量式
r ⃗ = R ( c o s ( w t ) i ⃗ + s i n ( w t ) j ⃗ ) \vec{r}=R(cos(wt)\vec{i}+sin(wt)\vec{j}) r=R(cos(wt)i+sin(wt)j)
轨迹方程
x 2 + y 2 = R 2 , z = 0 x^2+y^2=R^2,z=0 x2+y2=R2,z=0
自然坐标中的速度和加速度
速度
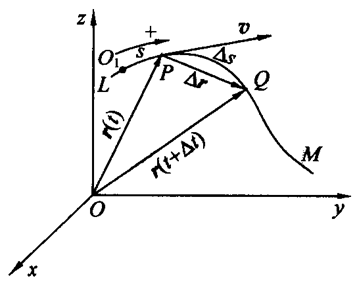
线速度: v ⃗ = lim Δ t → 0 Δ r ⃗ Δ t = lim ( Δ r ⃗ Δ s Δ s Δ t ) = ( lim Δ r ⃗ Δ s ) ( lim Δ s Δ t ) \vec{v}=\lim_{\Delta t\to 0} \frac{\Delta \vec{r}}{\Delta t}=\lim(\frac{\Delta \vec{r}}{\Delta s}\frac{\Delta s}{\Delta t})=(\lim\frac{\Delta \vec{r}}{\Delta s})(\lim\frac{\Delta s}{\Delta t}) v=Δt→0limΔtΔr=lim(ΔsΔrΔtΔs)=(limΔsΔr)(limΔtΔs) ( lim Δ t → 0 Δ r ⃗ Δ s ) = d r ⃗ d s = τ ⃗ (\lim_{\Delta t\to 0}\frac{\Delta\vec{r}}{\Delta s})=\frac{d\vec{r}}{ds}=\vec{\tau} (Δt→0limΔsΔr)=dsdr=τ v = lim Δ t → 0 Δ s Δ t = d s d t v=\lim_{\Delta t\to 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt} v=Δt→0limΔtΔs=dtds v ⃗ = v τ ⃗ = d s d t τ ⃗ \vec{v}=v\vec{\tau}=\frac{ds}{dt}\vec{\tau} v=vτ=dtdsτ
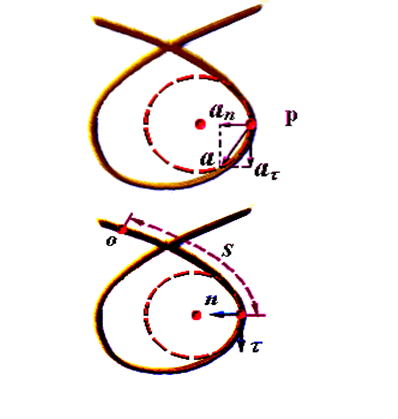
圆周运动加速度
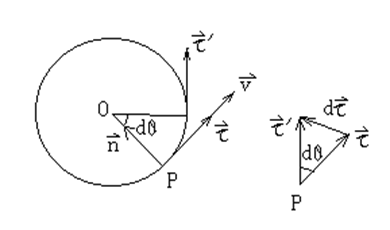
加速度: a ⃗ = d v ⃗ d t = d ( v τ ⃗ ) d t = d v d t τ ⃗ + v d τ ⃗ d t \vec{a}=\frac{d\vec{v}}{dt}=\frac{d(v\vec{\tau})}{dt}=\frac{dv}{dt}\vec{\tau}+v\frac{d\vec{\tau}}{dt} a=dtdv=dtd(vτ)=dtdvτ+vdtdτ其中: d τ ⃗ = ∣ τ ∣ d θ n ⃗ = d θ n ⃗ d\vec{\tau}=|\tau|d\theta\vec{n}=d\theta\vec{n} dτ=∣τ∣dθn=dθn d τ ⃗ d t = d θ d t n ⃗ = R d θ R d t n ⃗ = 1 R d s d t n ⃗ = v R n ⃗ \frac{d\vec{\tau}}{dt}=\frac{d\theta}{dt}\vec{n}=\frac{Rd\theta}{Rdt}\vec{n}=\frac{1}{R}\frac{ds}{dt}\vec{n}=\frac{v}{R}\vec{n} dtdτ=dtdθn=RdtRdθn=R1dtdsn=Rvn ⇒ a ⃗ = d v d t τ ⃗ + v 2 R n ⃗ = a τ τ ⃗ + a n n ⃗ \Rightarrow\vec{a}=\frac{dv}{dt}\vec{\tau}+\frac{v^2}{R}\vec{n}=a_{\tau}\vec{\tau}+a_n\vec{n} ⇒a=dtdvτ+Rv2n=aττ+ann
切向加速度: a τ = d v d t a_{\tau}=\frac{dv}{dt} aτ=dtdv
法向加速度: a n = v 2 R a_n=\frac{v^2}{R} an=Rv2
加速度大小: a = ∣ a ⃗ ∣ = a τ 2 + a n 2 a=|\vec{a}|=\sqrt{a_{\tau}^2+a_n^2} a=∣a∣=aτ2+an2
圆周运动的角量表示
角速度: ω = lim Δ t → 0 Δ θ Δ t = d θ d t \omega=\lim_{\Delta t\to 0}\frac{\Delta \theta}{\Delta t}=\frac{d\theta}{dt} ω=Δt→0limΔtΔθ=dtdθ
角加速度: α = lim Δ t → 0 Δ ω Δ t = d ω d t = d 2 θ d t 2 \alpha=\lim_{\Delta t\to 0}\frac{\Delta \omega}{\Delta t}=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2} α=Δt→0limΔtΔω=dtdω=dt2d2θ
角 速 度 ω ⃗ 方 向 : \red{角速度\vec{\omega}方向:} 角速度ω方向:按照“右手规则”确定,四个手指指向运动方向,大拇指方向便是角速度方向。
角 加 速 度 α ⃗ 方 向 : \red{角加速度\vec{\alpha}方向:} 角加速度α方向:加速时与 ω ⃗ \vec{\omega} ω方向相同,减速时与 ω ⃗ \vec{\omega} ω方向相反。
圆周运动中线量与角量的关系
线速度与角速度: Δ s = R Δ θ = > v = R ω \Delta s=R\Delta \theta=>v=R\omega Δs=RΔθ=>v=Rω
切向加速度与角加速度: a τ = R α ( 由 上 式 对 t 求 导 所 得 ) a_{\tau}=R\alpha(由上式对t求导所得) aτ=Rα(由上式对t求导所得)
法向加速度与角速度: a n = v 2 R = v ω = R ω 2 a_n=\frac{v^2}{R}=v\omega=R{\omega}^2 an=Rv2=vω=Rω2
速度分量式: v x = d x d t = d ( R c o s ω t ) d t = − R ω s i n ω t v_x=\frac{dx}{dt}=\frac{d(Rcos\omega t)}{dt}=-R\omega sin\omega t vx=dtdx=dtd(Rcosωt)=−Rωsinωt v y = d y d t = d ( R s i n ω t ) d t = R ω c o s ω t v_y=\frac{dy}{dt}=\frac{d(Rsin\omega t)}{dt}=R\omega cos\omega t vy=dtdy=dtd(Rsinωt)=Rωcosωt v = v x 2 + v y 2 = R ω v=\sqrt{v^2_x+v^2_y}=R\omega v=vx2+vy2=Rω
速度矢量式: v ⃗ = d r ⃗ d t = v x i ⃗ + v y j ⃗ = R ω ( − s i n ω t i ⃗ + c o s ω t j ⃗ ) \vec{v}=\frac{d\vec{r}}{dt}=v_x\vec{i}+v_y\vec{j}=R\omega(-sin\omega t\vec{i}+cos\omega t\vec{j}) v=dtdr=vxi+vyj=Rω(−sinωti+cosωtj)
加速度分量式: a x = d v x d t = − R ω 2 c o s ω t a_x=\frac{dv_x}{dt}=-R\omega^2cos\omega t ax=dtdvx=−Rω2cosωt a y = d v y d t = − R ω 2 s i n ω t a_y=\frac{dv_y}{dt}=-R\omega^2sin\omega t ay=dtdvy=−Rω2sinωt a = ∣ a ⃗ ∣ = a x 2 + a y 2 = R ω 2 a=|\vec{a}|=\sqrt{a^2_x+a^2_y}=R\omega^2 a=∣a∣=ax2+ay2=Rω2
匀变速率圆周运动
α = 常 量 , 故 : a t = r α , a n = r ω 2 \alpha=常量,故:a_t=r\alpha,a_n=r\omega^2 α=常量,故:at=rα,an=rω2 ω = ω 0 + α t \omega=\omega_0+\alpha t ω=ω0+αt θ = θ 0 + ω 0 t + 1 2 α t 2 \theta=\theta_0+\omega_0t+\frac{1}{2}\alpha t^2 θ=θ0+ω0t+21αt2 ω 2 = ω 0 2 + 2 α ( θ − θ 0 ) \omega^2=\omega_0^2+2\alpha(\theta-\theta_0) ω2=ω02+2α(θ−θ0)
一般平面曲线运动
对于这种曲线运动,曲率半径是变化的,通常是 ρ \rho ρ来表示。
a ⃗ = a ⃗ τ + a ⃗ n = a τ τ ⃗ + a n n ⃗ = d v d t τ ⃗ + v 2 ρ n ⃗ \vec{a}=\vec{a}_{\tau}+\vec{a}_n=a_{\tau}\vec{\tau}+a_n\vec{n}=\frac{dv}{dt}\vec{\tau}+\frac{v^2}{\rho}\vec{n} a=aτ+an=aττ+ann=dtdvτ+ρv2n a = ∣ a ⃗ ∣ = a τ 2 + a n 2 a=|\vec{a}|=\sqrt{a^2_{\tau}+a^2_n} a=∣a∣=aτ2+an2
对于匀速圆周运动: v = C , a τ = d v d t = 0 , a = a n = v 2 R v=C,a_{\tau}=\frac{dv}{dt}=0,a=a_n=\frac{v^2}{R} v=C,aτ=dtdv=0,a=an=Rv2
今天的文章经典力学学习(运动学)——圆周运动与一般平面曲线运动「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:http://bianchenghao.cn/83846.html