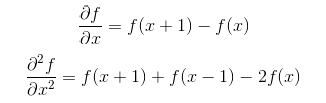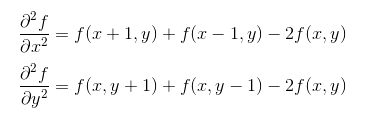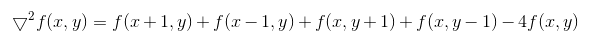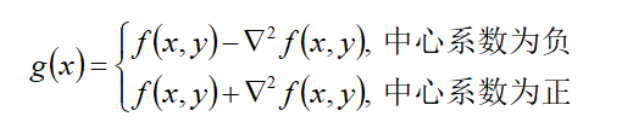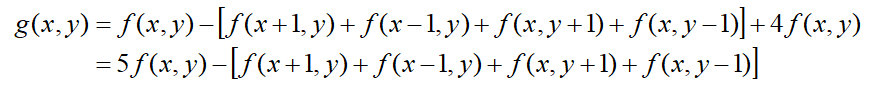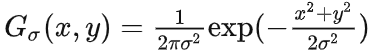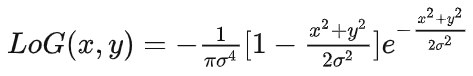高斯算子和拉普拉斯算子的卷积_Laplace算子

1.拉普拉斯算子

Laplace算子作为边缘检测之一，和Sobel算子一样也是工程数学中常用的一种积分变换，属于空间锐化滤波操作。拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度（▽f）的散度（▽·f）。

拉普拉斯算子是二阶微分线性算子，在图像边缘处理中，二阶微分的边缘定位能力更强，锐化效果更好，因此在进行图像边缘处理时，直接采用二阶微分算子而不使用一阶微分。

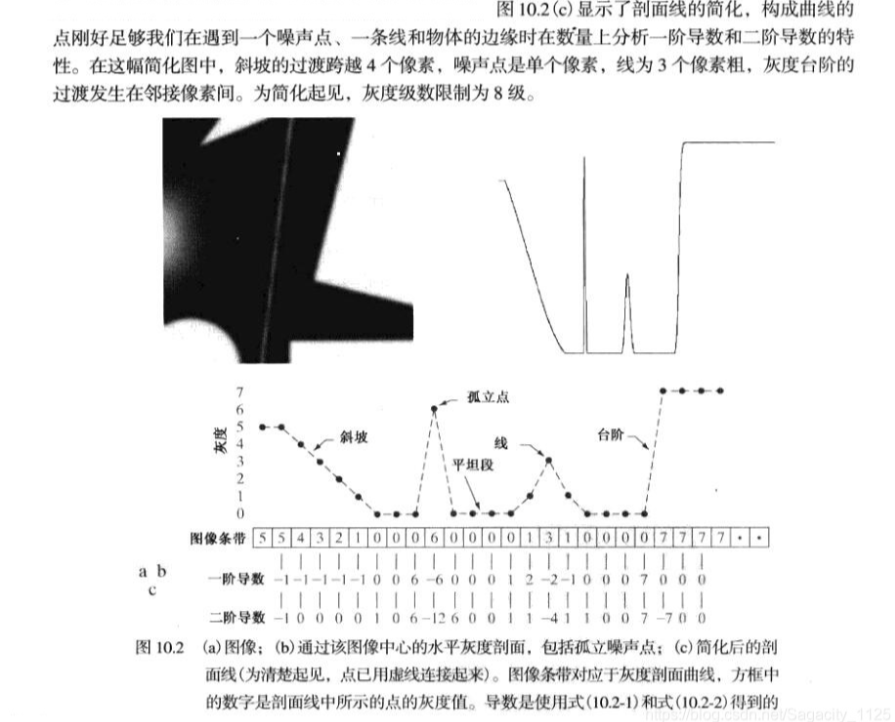
图1 一阶微分和二阶微分计算图

离散函数的导数退化成了差分，一维一阶差分公式和二阶差分公式分别为：

分别对Laplace算子x,y两个方向的二阶导数进行差分就得到了离散函数的Laplace算子。在一个二维函数f(x,y)中，x,y两个方向的二阶差分分别为：

所以Laplace算子的差分形式为：

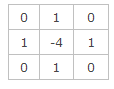
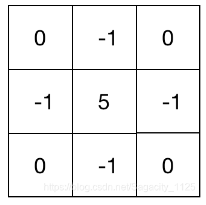
写成filter mask的形式如下：

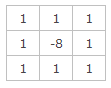
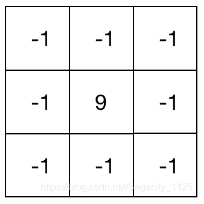
该mask的特点，mask在上下左右四个90度的方向上结果相同，也就是说在90度方向上无方向性。为了让该mask在45度的方向上也具有该性质，对该filter mask进行扩展定义为：

这里要注意一下：

当使用中心为负数，周围为正数的卷积核时，在较暗的一侧的卷积运算后的响应值是正数，而在较亮的一侧卷积运算后的响应值则为负数。

该卷积运算后的响应值不能直接叠加到原图上。

将Laplace算子写成filter mask后，其操作大同小异于其他的空间滤波操作。将filter mask在原图上逐行移动，然后mask中数值与其重合的像素相乘后求和，赋给与mask中心重合的像素，对图像的第一，和最后的行和列无法做上述操作的像素赋值零，就得到了拉普拉斯操作结果。因为Laplace算子是二阶导数操作，其在强调图像素中灰度不连续的部分的同时也不在强调灰度值连续的部分。这样会产生一个具有很明显的灰度边界，但是没有足够特征的黑色背景。背景特征可以通过原图像与Laplace算子操作后的图像混合恢复，公式如下：

 进一步推导如下：

写成filter mask的形式如下:

扩展定义为：

2.高斯-拉普拉斯算子

由于拉普拉斯算子对图片中的噪声很敏感。因此，为了解决这一问题，我们一般会在进行拉普拉斯操作之前先对图像进行高斯平滑滤波处理，得到高斯-拉普拉斯算子（LoG）。
高斯-拉普拉斯算子是效果更好的边缘检测器，它把高斯平滑器和拉普拉斯锐化结合起来。先平滑掉噪声，再进行边缘检测。
模版例子如下：

2.1简要描述

拉普拉斯算子是图像二阶空间导数的二维各向同性测度。拉普拉斯算子可以突出图像中强度发生快速变化的区域，因此常用在边缘检测任务当中。在进行Laplacian操作之前通常需要先用高斯平滑滤波器对图像进行平滑处理，以降低Laplacian操作对于噪声的敏感性。该操作通常是输入一张灰度图，经过处理之后输出一张灰度图。

2.2公式的由来

第一节的拉普拉斯算子都是对图片二阶导数的近似估计，它们对于图片中的噪声均很敏感。因此，为了解决这一问题，我们一般会在进行拉普拉斯操作之前先对图像进行高斯平滑滤波处理，二维的高斯平滑卷积核可以采用以下公式进行表示：

先利用高斯平滑滤波进行处理，可以降低图片中的高频噪声，方便后续的拉普拉斯操作。事实上由于卷积操作具有结合律，因此我们先将高斯平滑滤波器与拉普拉斯滤波器进行卷积，然后利用得到的混合滤波器去对图片进行卷积以得到所需的结果。采用这个做法主要有以下两个优点：

• 由于高斯和拉普拉斯核通常都比图像小得多，所以这种方法通常只需要很少的算术运算。
• LoG (‘ Laplacian of Gaussian’)内核的参数可以预先计算，因此在运行时只需要对图像执行一遍的卷积即可

以0为中心，高斯标准差为 sigma 的二维的LoG 函数的表达式如下所示：

具体的推导过程如下所示:

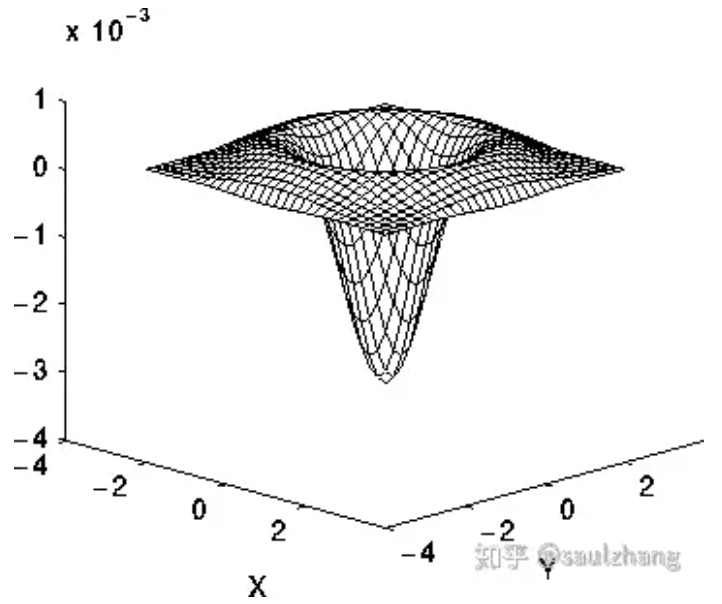
函数的图像如下图所示：

图2.二维LoG函数的图像，其中x轴和y轴是以标准差为单位的

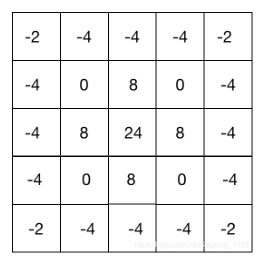
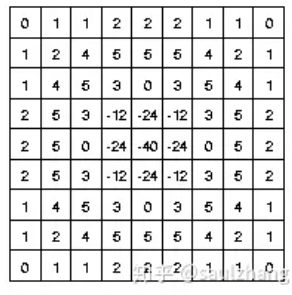
以下图3所示的离散卷积核可以近似上面的表达式(当 sigma=1.4 时)：

图3. 高斯标准差为1.4时，LoG函数的离散卷积核近似

值得注意的是，随着高斯函数变得越来越窄，LoG卷积核将会近似于图1中所示的简单Laplacian内核，主要原因是因为采用十分窄的高斯函数( sigma<0.5pixels )时，其在于离散的网格上面是不起作用的。因此，在离散的网格上，简单的拉普拉斯算子可以看成是一种高斯函数很窄的 LoG函数。

参考

Laplace(拉普拉斯)算子_拉普拉斯算子_Sagacity_1125的博客-CSDN博客

高斯拉普拉斯算子（Laplacian of Gaussian, LoG） – 知乎

今天的文章高斯算子和拉普拉斯算子的卷积_Laplace算子分享到此就结束了，感谢您的阅读。