逻辑学基本知识点_逻辑学讲什么内容呀「建议收藏」

逻辑学入门很简单 笔记 一些逻辑学常见概念

1. 概念

   • 从逻辑学的角度讲，概念是一种思维形式，而且是逻辑学首先需要研究的对象。如果说思维是一种生物，那么概念就是这种生物的细胞。概念是对客观存在辩证的反映，是主观性与客观性、共性与个性、抽象性与具体性的统一。同时，因为概念是可以相互转化的，所以概念也是确定性和灵活性的统一。
   • 概念是人们在认识事物的过程中，对“这种事物是什么”的回答。通常，人们都认为概念是反映对象的本质属性的思维形式。而且，它所反映的是一切能被思考的事物。

   1. 内涵：指这个概念的具体含义，就是事物“有什么特点“

      玫瑰花：外观是怎样的的，有什么特点，摸起来什么感觉，它的花是怎样的，味道怎么样，分布在哪里，生长周期有什么特点，可以用来干什么等

   2. 外延：指这概念包含了哪些事物，也就是“包含什么”

      玫瑰花：有哪些品种，白玫瑰？红玫瑰？

   3. 关系：

      1. 相容关系

      1.同一关系

      概念完全重合，也叫作全同关系

      “鲁迅”和“周树人”

      2.从属关系

      在两个概念a、b之间，如果a的所有外延都是b的外延，但是b的外延不全是a的外延，那么，a与b就构成了从属关系。

      “老年人”和“成年人”之间就构成了从属关系，因为所有的“老年人”都是“成年人”，但是“成年人”还包含了“中年人”等，

      “老年人”是“成年人”的种概念，对于“成年人”是种属关系，即“老年人”真包含于“成年人”；“成年人”是“老年人”的属概念，对于“成年人”是属种关系，即“成年人”真包含“老年人”。

      3.交叉关系

      如果在两个概念之间，它们的外延仅有一部分是重合的，而且各自的外延都有不重合的部分，那么，这两个概念之间就是交叉关系。

      “警察”和“男人”。警察有男警和女警，男人有老师，程序员，警察等众多职业，两者重合部分为男警察。

      2. 不相容关系

         1.矛盾关系

         对于a、b两个概念，如果它们的外延没有任何部分重合，并且对于它们共同的属概念c的外延来说，不是a，就是b，即c=a+b，那么，a与b之间就是矛盾关系。

         “男人”和“女人”。不是男人就是女人。

         2.反对关系

         对于a、b两个概念，如果它们的外延没有任何部分重合，并且对于它们的属概念c的外延来说，a与b的外延只是其中一部分，即c>a+b，那么，a与b之间就是反对关系。

         数：正数，负数，0

         则正数和负数为反对关系.

         其他关系

2. 直言命题

   1. 主项、谓项、联项、量项

   2. 联项：肯定命题，否定命题；量项：全称命题、特称命题、单称命题

   3. SAP：全称肯定命题

   4. SEP：全称否定命题

   5. SIP：特称肯定命题

   6. SOP：特称否定命题

   7. 判定真假：主项概念和谓项概念的外延

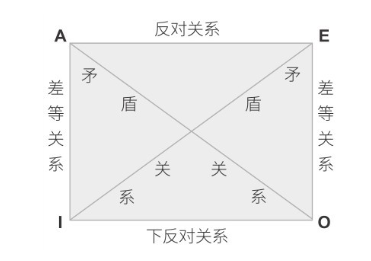
   8. 命题关系：

      (1)反对关系：如A和E之间，不能同真，可以同假。也就是说，已知其中一个为真，另一个就是假；或已知其中一个为假，另一个不确定。

      (2)差等关系（从属）：如A和I、E和O之间，如果特称命题为假，则相应的全称命题就为假；如果全称命题为真，则相应的特称命题就为真。

      (3)矛盾关系：如A和O、E和I之间，若其中一个为真，则另一个必定为假。

      (4)下反对关系：如I和O之间，不能同假，可以同真。也就是说，已知其中一个为假，则另一个就是真；或已知其中一个为真，则另一个不确定

3. 关系命题

   1. 关系项、关系、量项
   2. 判定真假
      1. 对称性：对称关系、反对称关系、非对称关系
      2. 传递性：传递关系、反传递关系、非传递关系

4. 复合命题

   1. 联言命题
      1. 不仅···而且···
      2. 既···又···
      3. 和···和···
      4. ···且···
   2. 选言命题
      1. 要么···要么···
      2. 或者···或者···
      3. 不是···就是···
   3. 假言命题
      1. 如果···就···
      2. 没有···就没有···
      3. ···当且仅当···
   4. 负命题
      1. A和非A

5. 三段论

   1. 主项S、谓项P、中间项M
   2. 大前提：MAP
   3. 小前提：SAM
   4. 结论：SAP
   5. 判定真假：周延
   6. 周延：
      1. 主项周延：看量项。全称命题为周延，特称命题为非周延
      2. 谓项周延：看联项。肯定命题为不周延，否定命题为周延

6. 复合推理

   1. 反三段论
   2. 假言三段论
   3. 假言联言推理
   4. 负推理
   5. 二难推理

7. 归纳推理

   1. 完全归纳推理
      1. 数学归纳法
   2. 非完全归纳推理
      1. 枚举推理
      2. 科学归纳法
   3. 统计推理

8. 类比推理

9. 因果关系

   1. 求同法
   2. 求异法
   3. 求同求异并用法
   4. 共变法
   5. 剩余法

10. 逻辑规律

    1. 同一律：A是A。论题同一，主项谓项的概念同一。
    2. 矛盾律：A不是非A
    3. 排中律：A和非A必有一真
    4. 理由充分律

11. 假设推理

    1. 假设部分条件合理，并据此推出结论，若结论出现矛盾则否决该假设；若合理，则继续进行下一条假设。不断循环，直至得到最终合理的答案。
    2. 混合问题：以提问的形式出现，且在问题中包含了某种预先进行的假设或者论断的逻辑错误

    你会不会再犯这种错误 $\Rightarrow$ 包含：你这次做的是错误的

    你知不知道你刚刚做了一件蠢事 $\Rightarrow$ 包含：你刚刚做的事是一件蠢事

    你接不接受这个正确的建议 $\Rightarrow$ 包含：这个建议是正确的

12. 论证

    1. 论点：也作论题。通常是一个表示某个观点的命题，而不能只是某个单独的概念。
    2. 论据：用来证明论点的依据，它一般都是客观性的理论原理或者一些客观的事实或者数据等。
    3. 论证方式：来将论点和论据联系起来的方式，也就是论证过程中从论据到论点的推理方式，表达的是论据是如何来证明论点的。
       1. 演绎论证
       2. 归纳论证
       3. 类比论证
       4. 因果论证
    4. 论证规则：
       1. 论点明确
       2. 论据相关
       3. 论证可靠

13. 反驳

    1. 反驳就是用一个或一些已知为真的命题并借助推理的过程来确定另一个命题是假命题或者另外一个论证不成立的思维过程。

    2. 反驳就是削弱对方的某个观点或者某种思想，找出对方论证过程中的疏漏或者错误。

    3. 反驳的对象：被反驳的对象可以只是单个的观点，也可以是对方论证中的论点、论据或者论证方式。

    4. 反驳的论据：反驳的论据指的是进行反驳的依据。它可以是一些已知的事实材料或者科学原理。

    5. 反驳方式：反驳方式指的是在反驳的过程中使用的推理形式。它是将被反驳的论点和反驳的依据连接起来的方式，从而构成一个反驳的整体。

    6. 反驳方法：

       1. 直接法：直接引用已知的事实或者原理进行反驳。直接法当中可以运用演绎推理，也可以运用归纳推理。

          “所有的鸟都会飞。不，鸵鸟是鸟，但它不会飞，而用双腿奔跑。” $\to$ 简单枚举法

       2. 间接法：论证与对方的论点矛盾或者相反的命题是正确的，也就得到了这个论点是错误的，从而达到了反驳的目的。利用排中律。

          “这个数是正数。不，这个数小于0，因而它是负数，所以它不是正数。”

       3. 归谬法：先假设对方的论点是成立的，然后按照对方的逻辑进行分析和推理，最后得到一个自相矛盾的或者荒谬的结论，这样也就说明了假设是不成立的，也就有力地反驳了对方的论点。类似于反证法，使用了假设的方法，利用了逻辑规律中的矛盾律，由对方逻辑在推理分析中出现前后矛盾的现象，也就得到了对方的逻辑是错误的。

          “施肥越多，庄稼长得越好。不，如果施肥过多的话，会导致土壤溶液的浓度过高，这个时候，就会烧伤根系，让庄稼枯萎，怎么会是长得越好呢？”

          在这个反驳的过程中，先是假设对方的观点是正确的，然后通过推理却得到了“庄稼枯萎”的相反结论，从而反驳了“施肥越多，庄稼长得越好”的观点。

今天的文章逻辑学基本知识点_逻辑学讲什么内容呀「建议收藏」分享到此就结束了，感谢您的阅读。