数量遗传学第四章有限大小的群体和近交

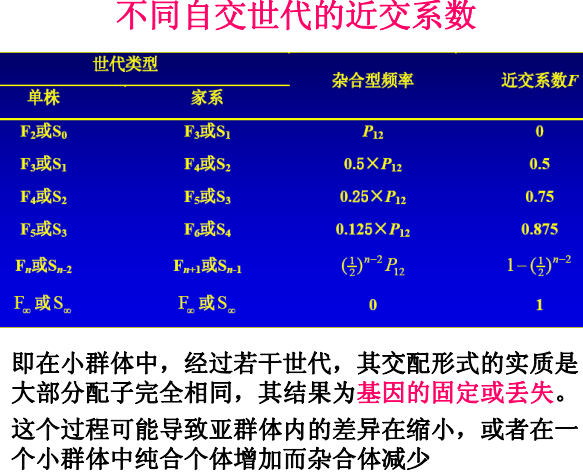
（Hardy-Weinberg平衡群体的条件和性质，连锁不平衡）

一、几个概念理解

名词	解释	说明
有限大小群体	样本个体不足够大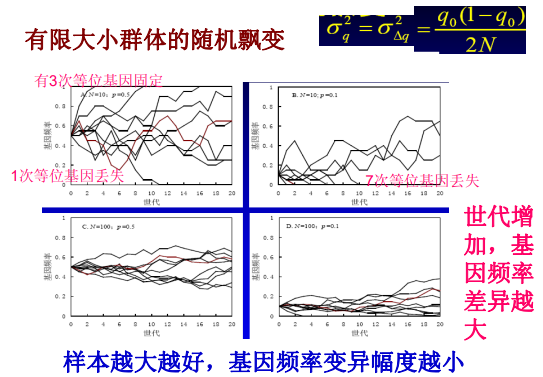
随机飘移 (random drift)	在小群体中对等位基因的频率产生较大的影响，且其方向不可预测。
近交 inbreeding	血缘关系较近的个体间交配	在两性生物的群体中，每个个体有两个亲本，四个祖先，八个曾祖先，追溯到第 t个世代以前，应有2t个亲本，当然在t较小、群体又相当地大时，还可以满足非近交的要求。在小群体中，因容量是有限的，所以群体内的个体间必定有某种程度的亲缘关系。一般地，在小群体中用不着追溯多久，就会发现某两个个体有共同的祖先。在小群体中，尽管交配是随机，但群体愈小，个体间的关系愈密切，所以有时小群体遗传性质可以近似看成为是自交交配系统。植物的自交和动物的同宗交配个体间的共祖先程度或者个体间血缘关系的密切程度与所在群体的大小有关。
理想群体 (Idealized population)	随机交配的大群体由于自然条件、地理或生活环境的变化而分为亚群体或人为选择的试验群体。原来的群体即基础群体或起始群体。亚群体即样本或品系。	随机交配的大群体由于自然条件或认为条件变为多个亚群体。理想群体产生的条件：1、小群体内发生交配，各小群体之间无迁移2、没有世代重叠3、各个小群体中，每个世代有相同数量的个体或具有生殖力的个体数相等4、群体内随机交配5、没有选择6、没有迁移和突变。
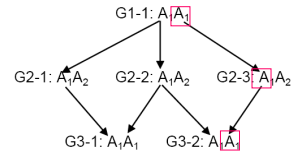
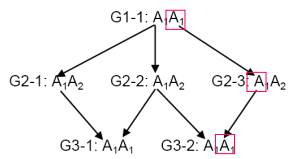
祖先关联 related by ancestry	具有共同祖先的个体间是祖先关联的。	G1-1的A1A1来源于不同祖先，因此，它们是状态相同，但不血缘同一。 G2-1 和 G2-的等位基因A1状态相同，而且是后裔同样的。
状态同一 identical by state	一个基因座上两个等位基因的相似性，但不管是否来自共同祖先。 A1A2，A1A1，A2A2
后裔同样 identity by descent IBD /血缘同一	子代的一段DNA或共有的等位基因来源于一个共同的祖先。
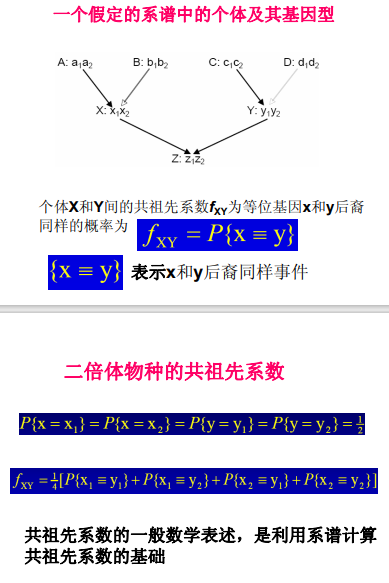
共祖系数 coancestry coefficient /=亲本系数 coefficient of parentage (fxy)	个体X和Y之间的共祖系数，在一个基因座位上，X 的一个随机等位基因与Y的一个随机等位基因后裔同样的概率.。	为某2个体所具有的同源基因/等位基因来自共同祖先的概率。反映两个亲本间的血缘关系和遗传差异。
近交系数 inbreeding coefficient F	个体X的某个基因座位上2个等位基因来源于共同祖先某个基因（后裔同样）的概率。	G1-1的A1A1来源于不同祖先，因此，它们是状态相同，但不血缘同一。G2-1和G2-2的等位基因 A1状态相同，而且是后裔同一的。对于考察的位点A1A2来说，G3-1的近交系数是 1，而G3-2的近交系数为0。
有效群体大小 Effective population size	群体中能将基因连续传递到下一代的个体平均数。	有方差有效群体大小和近交有效群体大小。有效群体大小是很多群体遗传学模型中的基本参量，通常小于绝对的种群大小（N）。
近交有效群体大小（Inbreeding effective population size	具有与当前群体相同近交系数的理想种群大小。	经历多个世代的种群大小由各世代个体数调和平均近交系数得出。
方差有效群体大小（Variance effective pop size）	和理想群体的等位基因频率具有相同方差的理想种群的大小	经历多个世代的种群大小由各世代个体数调和平均近交系数得出。

二、近交系数的估计

考虑某一位点的两个等位基因，小群体的容量为N，那么一共有2N个等位基因，那么在雌雄交配中，每个配子与其本身完全一样的配子结合的概率为1/2 N ，1/2 N定义为理想群体的近交系。ΔF=1/2N。

群体	近交系数
针对一个个体X的近交系数常用FX表示	近交系数FX等于个体X中一个基因座位上的两个等位基因是后裔同样的概率。 •FX=0，无近交（如无限大小随机交配群体） •FX=1，意味着完全近交（如自交系
理想群体近交系数的变化
有限大小理想群体中的近交系数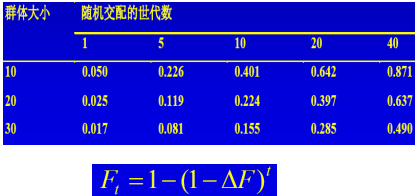

近交系数引起基因频率变化：理想群体的等位基因A1和A2频率为p和q，近交系数为F时，个体中后裔同样的两个等位基因常以纯合体形式出现，导致杂合型频率减少。F= [2pq-(2pq-2Fpq)]/2pq=1-P12(F)/P12。因此近交系数可以理解为近交引起的纯合体增加或杂合体频率所下降的比率。三种基因型频率：
A1A1 p2(1-F)+pF=p2+Fpq
A1A2 2pq(1-F)=2pq-2Fpq
A2A2 q2(1-F)+qF=q2+Fpq
近交系数等于由近交引起的杂合型频率相对于Hardy-Weinberg平衡的杂合型频率的变化。
近交系数计算：

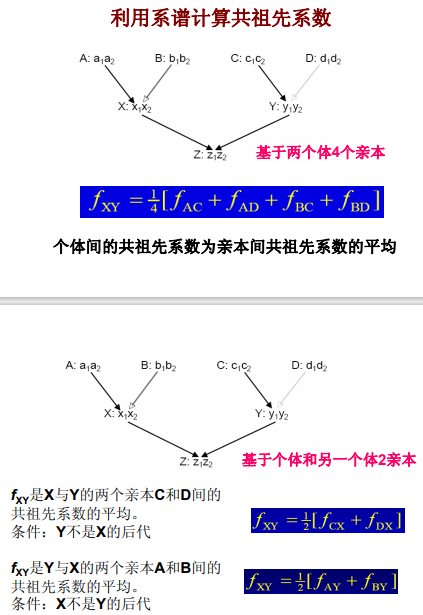
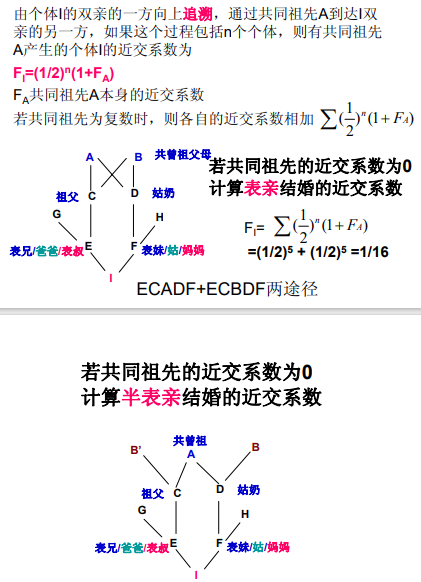
三、 Wright-Fisher模型是一个理想化群体模型
适用条件是：（1）二倍体生物；（2）群体内随机交配；（3）群体内性别比为1:1；（4）没有世代重叠现象，即认为上一代第一次完成繁殖任务后即死去或永久失去生育能力；（5）每个个体都有同等机会将自己的遗传信息传递给下一代，且不考虑突变和自然选择因素。

有效群体大小：在讨论有限群体随机交配时，我们假定它是一个包含N个体的理想群体，随机交配一代后，近交系数增加ΔF=1/2N。基因频率变化的方差为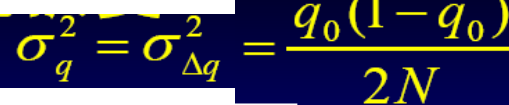。而实际上，这些在研的群体（育种群体）大多不是理想群体，为了能够像理想群体那样用基因频率的方差和近交系数去研究育种群体的分散过程，提出有效群体大小概念。美国遗传学家Sewall Wright (1931, 1938)引入了有效群体大小/有效种群大小。“ the number of breeding individuals in an idealized population that would show the same amount of dispersion of allele frequencies under random genetic drift or the same amount of inbreeding as the population under consideration”“在一个理想种群中，和｛该种群｛随机遗传漂变下的等位基因传播｝或者近亲繁殖｝等同的育种个体数量”有效群体大小：群体中能将基因连续传递到下一代的个体平均数。方差有效群体大小和近交有效群体大小。有效群体大小是很多群体遗传学模型中的基本参量，通常小于绝对的种群大小（N）。Ft=1-(1-ΔF)t每个个体随机交配，雌雄数相等。实际上，生物群体中不可能满足如此条件，即在N个体中平均只有Ne个体能有效将基因传递给下一代，Ne即群体大小。近交有效群体大小（Inbreeding effective population size) 具有与当前群体相同近交系数的理想种群大小Ne=1/2ΔF。经历多个世代的种群大小由各世代个体数调和平均近交系数得出。6个世代的种群大小为N=10，100，50，80，20，500 则Ne=1/2ΔF。调和平均=(1/10+1/100+1/50+1/80+1/20+1/500)/6*2 =0.1945/6*2=0.0324/2 ，Ne=1/0.0324=30.8。

常见育种群体的有效大小：

避免近亲交配的群体
公母个体数不等的群体（Nm 和Nf分别为雄雌个体数）
世代间个数不等的群体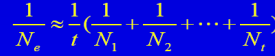
家系大小非随机分布的群体
常异花授粉物种的有效群体大小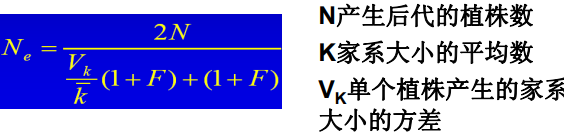
对自交率为s的群体
对随机交配群体
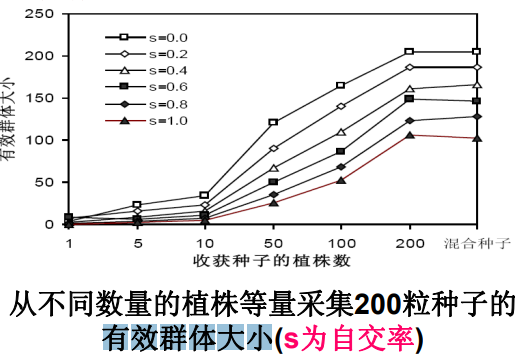
对混合群体抽样自交率s的群体