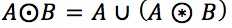opencv数学知识_opencv图像特征提取与识别

1.击中击不中运算

击中击不中（hit or miss）定义在交集为空集的两个结构元素的膨胀和腐蚀运算的基础上。设B =（B1，B2）表示结构元素对，且B1 ∩ B2 = ∅

则结构元素B对集合A的击中积补种运算，记做 

定义为：

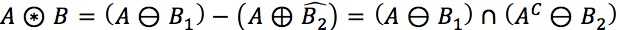
→运算过程为：

（→当且仅当B1平移某一z值包含在集合A的内部，也就是B1击中A且B2平移同一z值包含在集合A的外部（也就是B2击不中A），这个条件同时成立时，B的原点位置的集合。

→由于击中击不中运算B1和B2两个结构元素的交集为空集，也就是不会发生重合的现象，所以两个结构元素B1，B2可以拼成为一个单一结构元素B来进行表示。

→结构元素B对集合A的击中击不中运算结果是B1对A腐蚀结果和B2对A补集的腐蚀结果的交集。

→实际上可以看做是B在A中完全匹配的原点位置集合。

→击中击不中运算相当于一种条件比较严格的模板匹配

（→击中击不中运算的结构元素B也称为击中击不中模板

→作用：

击中击不中运算对于研究二值图像中前景目标与背景之间的关系非常有效。

 2.二值图像形态学的使用算法

二值图像形态学主要应用是提取度表示和描述形状有用的图像分量。

2.1 去噪

→二值化图像处理后经常会存在噪声，例如，孤立的前景噪声和目标区域中的小孔等等。

→如前所述，开运算和闭运算的结合处理是一种简单的图像去噪方法。

设A为二值图像，B为结构元素，去噪过程一般为先进行开运算在进行闭运算，可以表示为

à = （AοB）·B

→Ã 为去噪后的图像，根据目标形状和噪声的尺寸，应选择合适形状和尺寸的结构元素。

需要注意的是：

如之前所述，开运算和闭运算结合的形态学处理后会影响目标原本的边界和形状，特别是当目标本身尺度比较小时，这种去噪处理的方法很容易破坏边界的细节。

→对于复杂的边界目标，一般不建议使用这种形态学方法对二值图像进行后处理。

2.2 边界提取

结构元素B对集合A腐蚀的作用是收缩目标区域，集合A与腐蚀集合的差集，也就是说

边界提取的基本原理是 腐蚀运算移除的边界元素构成A的边界集合

可以表示为：

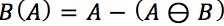
→B(A)表示集合A的边界集合，根据所需要的边界连通性和宽度，应选择合适尺寸和形状的结构元素。

→使用3×3方形结构元素可以提取但像素宽的4通道边界

→使用3×3菱形结构可以提取但像素宽的8联通边界

→使用5×5结构元素可以提取2~3个像素宽的4的边界

注意：

当结构元素B的原点位于或邻近图像外边界时，结构元素的一部分落在图像之外，常用的处理方法是假设图像边界外部均为背景像素，也就是0像素。

→与其他的边界跟踪算法相比，形态学边界提取算法简单而且容易实现，并且可以进行“并行处理”。

2.3孔洞填充（种子填充）

→孔洞指的是由连通的外界包围的背景区域。

→二值图像的孔洞填充的形态学算法是以集合的膨胀，补集和交集的组合形式定义的。

设集合A表示边界集合，B表示结构元素，给定边界内的一个点P（种子），初始化集合X0中点P所在位置值为1，其他位置为0

孔洞填充的过程可以表示为：

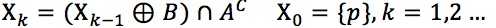
当Xk=Xk-1时在第k步迭代终止，这时Xk为孔洞填充的最终结果，Xk与其边界A的并集构成目标区域。

→若对膨胀不加以控制，则膨胀过程将会填充政府图像

→在每一次迭代过程中，与A补集进行交际将会膨胀集合限制在区域内部。这种在一定约束条件下的膨胀过程成为 条件膨胀

作用：

孔洞填充处理不会破坏目标原本的边界和形状，以此经常用于二值图像的后处理阶段，以便进行后续的目标形状，面积等图像分析工作。

2.4 连通分量提取

连通分量提取的形态学算法是以集合的膨胀和交集的组合形式定义的

→设y是集合A中的连通分量，B表示结构元素，给定连通分量y中的一个点p，初始集合X0中点p所在位置为1，其余的位置为0.

整个过程可以表示为：

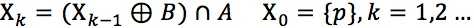
当Xk=Xk-1时，迭代中值，y=Xk为连通分量提取的最终结果

→条件膨胀通过与集合A交集将膨胀剂和限制在连通分量的内部

→对于8连通分量的提取，→使用方形的结构元素进行条件膨胀

→对于4连通分量的提取，→使用菱形的结构元素进行条件膨胀

在二值图像后处理中通常需要移除小目标（噪声分量）的干扰，除了使用结合开运算与闭运算方法外，也可以这样进行操作：

→提取二值图像中所有连通分量，计算各个连通分量的像素数，像素数小于某一值域的连通分量中像素赋值为0.

2.5 骨架

骨架是指在不改变目标拓扑结构的条件下，利用单像素宽的细线表示目标，→目标的骨架和目标本身具有相同数量的连通分量和孔洞。

→目标的骨架保持了了目标的欧拉数（空洞区域内空洞数量的度量）

→形态学骨架指的是利用二值图像形态学的方法提取出目标的骨架

设A表示集合，B表示结构元素，一种形态学骨架计算由下式给出

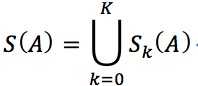
→集合A的骨架S(A)由骨架子集Sk(A)构成

→骨架子集Sk(A)定义在腐蚀和开运算组合形式的基础上，其计算公式为：

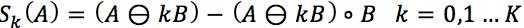
其中，AΘkB表示结构元素B对集合A的连续k次腐蚀，k为骨架子集的计算次数，数学表达式为

K=max{k | A Θ kB ≠ ∅}

→也就是说，k表示结构元素B将集合A腐蚀成为空集之前的最大次数，也就是一旦超过k次迭代，结构元素B将把集合A腐蚀成为空集。

注意：

骨架重构的过程是可逆的。→集合A可以利用骨架子集Sk(A)记性重构，计算公式为：

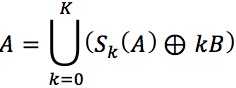
→式中，括号中的部分表示结构元素B对骨架子集Sk(A)的连续k次膨胀

注意：

这种算法提取到的骨架并没有达到最大限度的细化。

→由于在骨架提取的计算式中并没有任何条件保证最终结果的连通性→这种算法提取的骨架并不具有连通性

2.6 细化

细化是在保持目标连通性和边界几何特征条件下，利用线状结构来表示图像中的连通分量。细化的过程是不断伤处目标区域的边界像素

→用将目标区域细化成为单像素宽的线状结构来表示。

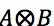
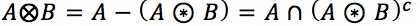
→结构元素B对集合A的细化，记做，它是定义在击中击不中运算的基础上，具体的计算式如下：

式中，等号左边表示的是以此独立的细化操作，定义一组结构元素B = {B1,B2,…,Bn}，使用结构元素B中的所有元素连续作用于集合A

→Bi为Bi-1旋转角度的形式

→整个过程以此使用结构元素B1，B2,…,Bn执行独立的细化操作，后一次是在前一次结果上的继续执行细化操作。

→根据上式完成一组结构元素成为一次迭代，反复进行迭代，知道不再发生变化位置，这时，目标区域删成为但像素宽的细线。

2.7 粗化

→粗化是细化在形态学上是对偶过程，结构元素B对集合A的粗化，记做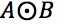，也是定义在击中击不中运算的基础上。

计算式为：

上式表以此独立的粗化操作过程

→定义一组结构元素B = {B1,B2,…,Bn}，使用结构元素B中的所有元素连续作用于集合A

今天的文章opencv数学知识_opencv图像特征提取与识别分享到此就结束了，感谢您的阅读。