离散数学知识点汇总_离散数学学的是什么

命题的判断

• 陈述句
• 能够唯一判定其真值
• 命题真值为真，则本命题是个真命题
• 命题真值为假，则本命题是个假命题
• 命题是命题逻辑中最小的不可再分的单元。

Note：命题的真值，可以理解为命题描述的这个意思~

Example：

张三是法外狂徒。

• 是个陈述句
• 法外狂徒是张三的属性，是这个命题的真值
• 如果张三真是个法外狂徒，那么这是个真命题
• 如果张三不是个法外狂徒，代表这个命题的真值是假的，是个假命题

Example2：

我说的话是假话

• 是个陈述句
• 假话是这句话的属性，也是这个命题的真值。
• 但是这个命题的真值没办法被唯一确定
• 因为如果这句话确实是句假话，那么这个命题是真的，而且这句话确实是句假话，那就与命题相悖；
• 因此无法唯一确定这个命题的真值，因此这不是个命题。

命题的表示

• 一个命题通常用小写字母来表示，比如用 $p$ 来表示：“张三是法外狂徒”；
• 同样的也可以用 $q$ 来表示 “今天要下雨” 这个命题。

复合命题

• 用 “联结词” 修饰的命题，或是连接不同命题，使其成为复合命题。
• 复合命题可以没有现实逻辑的意义。只要符合命题逻辑符号的规范，我们都认为是没有问题的。

Example：
如果 张三是法外狂徒，那么 明天会下雨

• $p$ ：“张三是法外狂徒”；
• $q$ ： “今天要下雨”
• $p\to q$
• 这就是个复合命题。

联结词的种类

除了上述的 $\to$ “单条件蕴含” 之外，还有以下联结词符号。

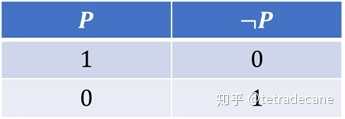
$￢$ 否定

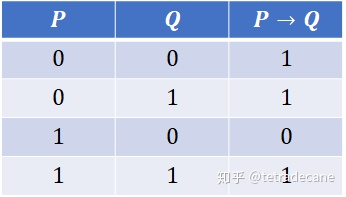
$\to$ 单条件蕴含

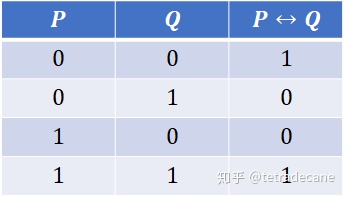
$\leftrightarrow$ 双条件蕴含

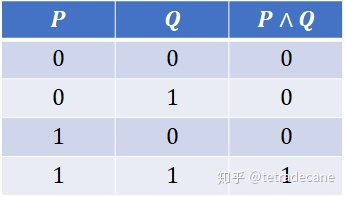
$\wedge$ 合取公式

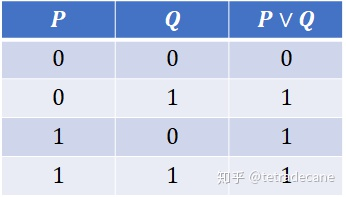
$\vee$ 析取公式

真值表

对于单纯的简单命题 $p$ 来说，它的命题真值只可能有两个，要么 $T$ 要么 $F$
对于复合命题来说，就不同了：

Example

• $p$
• $q$
• $p\to q$

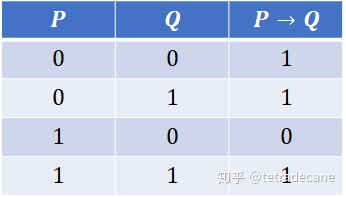
就这个复合命题来看。$p$ 一定是真命题么？不一定，$q$ 一定是真命题么？ 也不一定；

所以， $p\to q$ 这个复合命题，在什么情况下才是真命题呢？

按照常理，$p,q$ 都有两种情况，那么这个复合命题的结果可能有四种情况；让我们列个表看一下（T 表示1， F 表示 0）：

其实下面这种情况是 前人早就规定好的 。即当两个命题之间存在 单条件蕴含关系 的时候，只有一种情况会导致复合命题是假命题，即，前面的命题为真，后面命题为假（图中第三行）；其他假设条件下，这个复合命题 $p\to q$ 都是真命题。

按照前人的规定，在这里列出所有的基本运算的真值表情况；方便后面计算

$￢$ 否定

$\to$ 单条件蕴含

$\leftrightarrow$ 双条件蕴含

$\wedge$ 合取公式

$\vee$ 析取公式

Note：合取公式和析取公式很有意思，具有互补的感觉。合取只有一种情况为真，那就是两个简单命题都为真，而析取只有一种为假，那就是两个简单命题都为假

双条件蕴含和单条件蕴含也存在有趣的关系，单条件蕴含只有 $p$ 真，$q$ 假的时候为假，而双条件蕴含除此之外，还在 $p$ 假，$q$ 真的时候也为假。

今天的文章离散数学知识点汇总_离散数学学的是什么分享到此就结束了，感谢您的阅读。