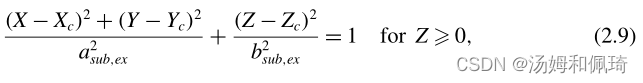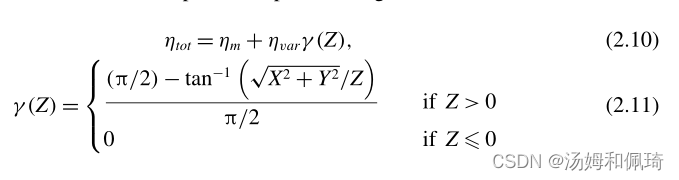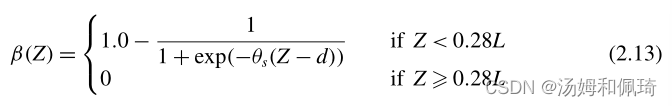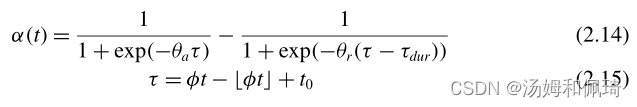水母模型_水螅模型立体制作教程

用主动游泳的三维水母模型量化美杜莎的（medusan）机械空间的性能（一）(2017)

原文链接：https://doi.org/10.1017/jfm.2017.3

这是一篇关于水母的三维运动模拟仿真的一篇文章，这篇文章的内容较多打算分成三篇进行逐一翻译，我一直在想在太空中是否存在这种类似于水母在水中运动的生物，我猜应该是存在的，哈哈。

摘要

  在许多游泳和飞行动物中，推进力来自主动肌肉收缩、被动身体弹性和流体-身体相互作用的相互作用。主动和被动物体特性的变化会在很大范围内影响运输的性能和成本；它们特别影响涡流的产生，这对于在较高雷诺数下的有效游泳是至关重要的。需要解释主动收缩和被动弹性的理论模型来理解动物如何调整它们的主动和被动属性，以有效地通过流体。当考虑到水母机械空间的系统发育限制时，这一点尤为重要，例如只有一个细胞层厚的相对较弱的肌肉的存在。在这项工作中，我们开发了一个浸入粘性流体中的水母的主动变形模型，并使用数值模拟来研究主动肌肉收缩、被动身体弹性和流体力在水母力学空间中的作用。通过改变收缩的强度和钟形边缘的柔韧性，我们量化了这些主动和被动的特性如何影响游泳速度和运输成本。我们发现，在弹力固定的情况下，游泳速度随着收缩强度的增加而增加。对于固定的收缩力，游泳速度随着边缘弹性的减小而增加。与钟形边缘的弹性成比例地改变激活的强度产生了相似的游泳速度，对于更灵活的边缘，运输成本显著降低。比例研究表明，性能随着雷诺数的降低而下降。对起始涡环和停止涡环的环流分析表明，它们的强度取决于相对于钟形边缘柔性的激活强度。这项工作为发展游泳中主动和被动身体属性的作用的定量理解提供了一个计算框架。生

关键词

  物流体动力学、推进、游泳/飞行

1. 引言

  拥有可追溯到中寒武纪的化石记录 (Cartwright et al. 2007)，水母是活跃的多细胞有机体的最早例子之一，并为肌肉驱动游泳的起源提供了一个窗口。缺乏主动-拮抗肌，水母推进力来自游泳肌肉的主动收缩、钟形结构的被动弹性再膨胀和周围流体作用于有机体的力之间的相互作用 (Demont & Gosline 1988b; Megill 2002; Megill, Gosline & Blake 2005; Hoover & Miller 2015)。水母通过收缩它们冠向的膜下游泳肌肉开始它们的游泳周期，这使它们的钟变形并从钟的内腔排出流体。中胶层是一种由类似胶原蛋白的纤维组成的细胞外基质，储存收缩产生的潜在弹性能量，并在游泳肌肉放松时驱动钟形结构的重新扩张。因为钟的静止形状取决于中胶层基质，水母推进被视为主动变形和弹性反冲的过程。
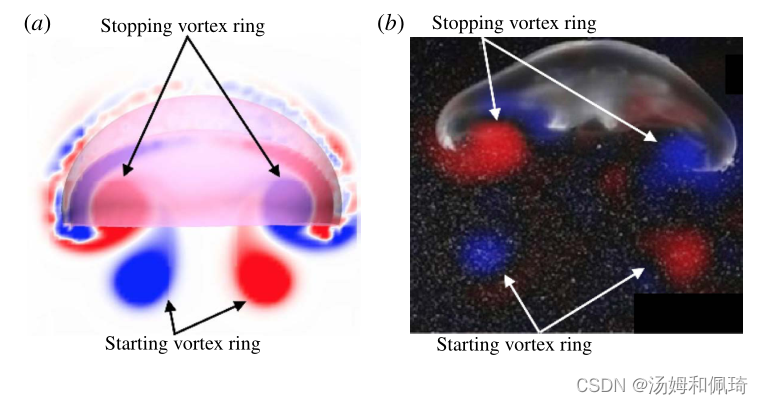
  最近，发现水母游泳时产生的尾流结构取决于钟的细度比，即钟状物高度与钟状物直径之比。扁长水母具有较高的浮力比，使用喷射推进来产生推力，而扁长水母具有较低的浮力比，使用划水机制，利用钟形膨胀时产生的涡环 (Dabiri，Colin & Costello，2007年)。这一发现解决了水母在较大体型时如何在只维持单层肌肉的情况下产生显著推力的问题 (Daniel 1983; McHenry & Jed 2003; McHenry 2007)。Dabiri等人(2007年)还发现，只要细度比小于约0.265，无论大小，划桨手都会产生显著的推力。在划桨的情况下，在钟声的收缩和随后的扩张过程中，相反旋转的起始涡环和停止涡环彼此远离，起始涡流离开钟声，停止涡流进入钟腔；见图1。二次推力是由钟形空腔中的停止涡产生的，没有额外的代谢成本。在下一个脉冲期间，新的起始涡流与先前形成的停止涡流一起平流离开钟形罩。这些交替的涡流对的相互作用增加了流体从水母的净输送，提供了一个增强的推力。
  除了流体动力学，泳钟的弹性特性对水母的游泳性能也很重要。Lucas等人最近的工作(2014)对大量可弯曲的附肢进行了采样，并揭示了增强推力产生的弯曲规律，这些规律超越了流体介质、动物大小和系统发育背景。实验观察Aurelia spp. 并结合机械模型模型发现，在增强推力产生的背景下进行了水母钟形边缘的灵活性的研究 (Colin et al. 2012; Gemmell, Costello & Colin 2014)。在这项工作中，指出钟形边缘在二次推力形成中起着很大的作用。在膨胀阶段，停止涡最初形成在钟罩的伞外表面，随后沉积在钟形腔中。如果钟形边缘太硬，涡流不会沉积在钟形中，这会减少被动能量重新捕获，并导致更高的运输成本 (Gemmell et al. 2013)。
  以前的建模工作也表明，当水母的泳钟以其共振频率驱动时，它们游得更快、更有效率 (Demont & Gosline1988b; Megill 2002; Megill et al. 2005; Hoover & Miller 2015) 。在所有这些研究中，一个正弦力被施加到钟形件上，使得收缩和扩张阶段都被主动驱动。Hoover & Miller (2015)研究了均匀刚度的二维长钟形背景下的共振驱动。在很宽的驱动频率和刚度范围内测量了游泳速度，并且当以共振频率驱动钟时，在向前的游泳速度和径向位移中发现了峰值。
  虽然计算流体动力学已被广泛用于检查水母的运动，但大多数先前的研究没有直接考虑泳钟的弹性，而是规定了它的运动 (Sahin, Mohseni & Colin 2009; Hamlet, Santhanakrishnan & Miller 2011; Herschlag & Miller 2011; Alben, Miller & Peng 2013; Hoover & Miller 2015)。这种方法的主要限制是，它不能完全解释材料属性、肌肉收缩的力学和钟形形态如何决定最终的运动。例如，Alben等人(2013年)研究了水母在规定运动学参数空间内的游泳效率。这项研究不能解决钟的弹性设计如何在向前游泳或操纵中有效地产生这种运动学的问题。
  当考虑限制水母机械空间和形态空间的系统发育限制时，上述问题变得重要。水母钟由外表皮层和内胃真皮层组成，每一层都只有一个细胞层厚。中胶层是由复杂的支持纤维网络组成的非细胞层，夹在两层之间。在大多数镰形动物中，包括月水母，冠状游泳肌肉是用于向前游泳的主要肌肉。这些是单层厚的肌上皮细胞。可以生成以使钟形变的最大可能力受该约束的限制，并且钟形边缘必须相对灵活以允许较大的变形。
  为了开始解决这些集中在弹性和肌肉特性上的基本问题，我们开发了一个完全耦合的三维模型来研究扁平水母的前向游泳。钟的向前运动完全由主动和被动的材料性质以及产生的流体-结构相互作用决定。求解这一问题的数值方法是基于浸没边界法，采用大变形连续介质力学框架来描述钟形结构。运动是由施加的主动张力驱动的，该张力模拟了冠状游泳肌的收缩。特别是，没有规定钟形的运动，也没有施加任何力量来纠正钟的轨迹。建立了一个材料模型，该模型考虑了钟的主动肌肉和被动弹性特性的空间变化。
  我们的研究集中在一种具有Autrlis aurita特征的典型的钵水母模型上。钟的自由振动频率保持大于驱动频率ω，以确保钟在下一次收缩之前完全膨胀。鉴于冠状肌肉在游泳中的主导作用，我们在这里忽略了放射状肌肉，放射状肌肉被认为主要在这些水母的转向中发挥作用 (Gemmell et al，2015b)。我们保持钟形顶部的刚度不变，与该区域的厚中胚层一致。鉴于水母肌肉只有一个细胞层厚的显著限制，我们探索了游泳肌肉产生的最大张力和钟形边缘弹性之间的关系。特别令人感兴趣的是，是否存在与使用相对灵活的钟形边际相关的成本，这种边际可能重新扩张缓慢，但很容易收缩。。
  最后，这个模型允许我们考虑完全三维的水母，它既不是纯二维的，也不是轴对称的。以前的近似可能会改变游泳的物理学，不允许人们考虑非轴对称过程，如转弯和操纵。例如， Herschlag&Miller(2011) 发现，尽管二维扁铃几何形状的流动轮廓和游泳速度可以用实验数据进行验证，但对于扁铃的二维模型，类似的验证失败了。Park等人(2014)在他们的模型水母钟上强加的运动方程中考虑了轴对称铃铛的弹性性质，但不能探索转弯、横流和剪切的影响或水母并排游泳的相互作用。

图1 (a)由我们的水母游动计算模型产生的启动和停止涡环的平面外涡度的快照。注意涡环对之间的相反旋转，其中红色对应顺时针涡度，蓝色对应逆时针涡度。起始涡环是在收缩阶段产生的，并离开钟声。停止涡环是在膨胀阶段产生的，产生二次推力。(b)启动和停止涡环的实验测量。来自Gemmell等人(2015b)。

2. 材料和方法

2.1 流固耦合

  流体-结构相互作用问题是生物系统中常见的问题，已经用各种计算框架进行了研究。浸没边界(immersed boundary，IB)方法 (Peskin 2002；Mittal&Iaccarino 2005) 是Peskin为研究心脏中的血液流动而引入的一种流体-结构相互作用的方法。从那时起，IB方法已经被应用于各种中低雷诺数区域的流体-结构相互作用系统，包括波动游泳 (Fuci&Peskin 1988；Bhala et al)。昆虫飞行 (Miller&Peskin 2004、2005、2009；Jones et al. 2015)，七鳃鳗游泳 (Tytell et al. 2010)，甲壳类游泳 (Zhang et al. 2014) 和水母游泳 (Hamlet et al. 2011；Herschlag&Miller 2011；hoover&Miller 2015)。
  流体-结构相互作用的IB公式用欧拉描述流固耦合系统的动量、粘性和不可压缩性，用拉格朗日描述结构的变形和应力。设 $x=(x，y，z)\in \Omega$ 表示物理笛卡尔坐标，$\Omega$ 表示流体-结构系统占据的物理区域。设 $\mathbf{X}=(X，Y，Z)\in U$ 表示附着到结构上的拉格朗日材料坐标，$U$ 表示拉格朗日坐标域。物质点$\mathbf{X}$在时间t的物理位置是 $\text{χ}(\mathbf{X}，t)\in \Omega$，因此结构在时间t占据的物理区域是 $\text{χ}(U，t)\in \Omega$。
  运动方程的浸没边界公式为：

$$\begin{array}{c}\rho (\frac{\partial \mathbf{u}(\mathbf{x},t)}{\partial t}+\mathbf{u}(\mathbf{x},t)\cdot \nabla \mathbf{u}(\mathbf{x},t))=-\nabla p(\mathbf{x},t)+\mu {\nabla }^2\mathbf{u}(\mathbf{x},t)+\mathbf{f}(\mathbf{x},t)\end{array}\text{\hspace{1em}(2.1)}$$
$$\begin{array}{c}\nabla \cdot \mathbf{u}(\mathbf{x},t)=0\end{array}\text{\hspace{1em}(2.2)}$$
$$\begin{array}{c}\mathbf{f}(\mathbf{x},t)={\int }_U\mathbf{F}(\mathbf{X},t)\delta (\mathbf{x}-\text{χ}(\mathbf{X},t)d\mathbf{X})\end{array}\text{\hspace{1em}(2.3)}$$
$$\begin{array}{c}{\int }_U\mathbf{F}(\mathbf{X},t)\cdot \mathbf{V}(\mathbf{X})d\mathbf{X}=-{\int }_U\mathbb{P}(\mathbf{X},t):{\nabla }_{\mathbf{X}}\mathbf{V}(\mathbf{X})d\mathbf{X}\end{array}\text{\hspace{1em}(2.4)}$$
$$\begin{array}{c}\frac{\partial \text{χ}(\mathbf{X},t)}{\partial t}={\int }_{\Omega }\mathbf{u}(\mathbf{x},t)\delta (\mathbf{x}-\text{χ}(\mathbf{X},t))dx\end{array}\text{\hspace{1em}(2.5)}$$
  其中 $\rho$ 是流体密度，$\mu$ 是动态粘度，$\mathbf{u}(\mathbf{x},t)=(u_x,u_y,u_z)$ 是欧拉物质速度场，$p(\mathbf{x},t)$ 是欧拉压力场。这里，$\mathbf{f}(\mathbf{x},t)$ 和 $\mathbf{F}(\mathbf{X},t)$ 是等价的欧拉力密度和拉格朗日力密度。$\mathbf{F}$ 定义为(2.4)中第一个Piola-Kirchhoff固体应力，其中$\mathbf{V}(\mathbf{X})$ 是任意拉格朗日检验函数。狄拉克增量函数$\delta (\mathbf{x})$ 是连接欧拉和拉格朗日标架的积分变换的核心，即方程(2.3)和(2.5)。
  在这项研究中，使用IB方法的有限差分/有限元混合形式来逼近方程(2.1)-(2.5)。这种IB/FE方法使用欧拉方程的有限差分格式和描述固体的有限元格式。关于IB/FE方法的更多细节可以在Griffith&Luo(2012)中找到。

下面的公式直接截图了，太难敲了，哎！

2.2 材料模型和钟形几何

  结构模型既考虑了钟的被动弹性属性，也考虑了肌肉产生的主动张力。利用第一Piola-Kirchoff应力张量计算了弹性体的结构应力：

其中 ${\mathbb{P}}_e$ 描述了身体的被动弹性，${\mathbb{P}}_a$ 描述了肌肉产生的主动张力。
  使用新虎克材料模型描述了中胶层的被动弹性性质:

其中 $\mathbb{F}=\partial \text{χ}/\partial \text{X}$ 是变形梯度，${\eta }_{tot}$ 是材料的弹性模量。
  一个依赖于时间的主动应力模拟了肌膜下游泳肌肉的肌肉激活。该应力沿圆周方向施加在钟形件的下部。主动应力通过下式计算:

其中 $J=det(\mathbb{F})$ 是 $\mathbb{F}$ 的雅可比，$T$ 是规定张力的大小，$f_0$ 是规定张力相对于参考构型的(纤维)方向矢量。这里选择 $f_0$ 来模拟未变形配置中的膜下游泳肌肉组织的冠状方向。这种建模方法的一个重要特征是钟形运动是主动张力、被动弹性和周围流体相互作用的结果。
  在这项研究中，开发了一个钟的三维模型，该模型考虑了钟形态的变化。以前的模型 (Daniel 1983;McHenry & Jed 2003; Sahin et al. 2009; Herschlag & Miller 2011) 将钟形几何描述为半椭球体，或使用函数拟合数字化钟形。这些方法已经在IB模拟中使用，将钟模拟为一维纤维的集合 (Daniel 1983;McHenry & Jed 2003; Sahin et al. 2009; Herschlag & Miller 2011) 。与基于纤维的IB模型相比，本文介绍的浸入体模型具有有限的体积、外膜和膜下表面以及灵活的边缘瓣。钟形通过外膜(ex)和膜下(sub)表面的半椭球描述进行参数化

其中 ${\mathbf{X}}_c=(X_c，Y_c，Z_c)$ 是椭球的中心， $a_{sub,ex}$ 分别是钟的亚膜表面和外膜表面的径向轴，$b_{sub,ex}$ 是垂直轴。受McHenry & Jed (2003)的启发，钟增加了一个均匀厚度的附加环，以模拟长度为$d$的钟边缘。
  弹性钟形模型考虑了钟形框的弹性边缘和钟形框其它区域之间的刚度差异。在该模型中，钟形件上材料点X处的弹性模量 ${\eta }_{tot}$ 取决于其高度

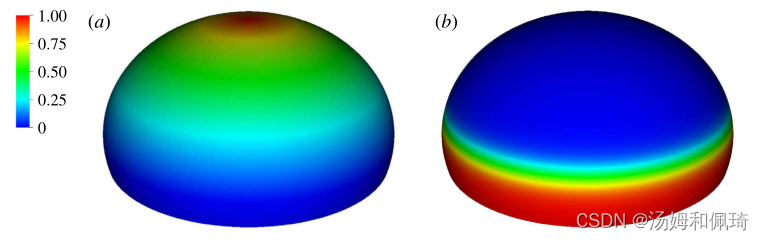
其中 ${\eta }_m$ 为钟形边的弹性模数，${\eta }_{var}$ 为钟形顶端的弹性模数与钟形边的弹性模数之差。钟形边缘的弹性模数是均匀的(见图2a)。

图2.(a)无因次归一化刚度γ和(b)无因次归一化主动张力β的空间组织。请注意，当一个人从铃铛的顶部移动到边缘时，有效刚度会降低。还要注意的是，铃铛的活动部分覆盖了铃铛的下部三分之一，并且是一种平滑的功能，使得顶部部分的张力为零。

  在选择施加主动张力的区域以及施加张力的持续时间和大小时要小心，以使张力的施加在空间和时间上是连续的。我们的方法是将张力 T 指定为随时间 t 变化的函数，以及钟形参考构形中的垂直空间分量 Z，使得

其中 $T_{max}$ 是最大应用张力，$\alpha (t)$ 是肌肉张力激活和释放的时间参数，$\beta (Z)$ 是伞下肌肉分布的空间参数。我们注意到 $0\le \alpha (T)，\beta (Z)\le 1$。值0意味着没有肌肉存在，或者肌肉没有被激活。
  伞下肌肉不会延伸到整个钟腔，所以主要是在钟口的边缘施加张力。激活区域通过以下方式进行参数化

其中 $L$ 是钟的特征长度，这里设置为伞外直径， ${\theta }_s$ 表征从主动张力区到不施加张力区的转变(见图2b)。
  张力被用来诱导前向游泳周期的收缩阶段。描述张力的激活和释放的功能来自于肌肉收缩的记录。发现于文献中 (Horridge 1954) ，并通过

其中 $\varphi$ 是游泳周期的频率， $t_0$ 是初始功能的偏移时间，${\theta }_a$ 表征肌肉激活的速度，${\theta }_r$ 表征张力的释放，${\tau }_{dur}$ 描述收缩的持续时间。

2.3 雷诺数

  这项工作的一个组成部分是量化尺度对游泳速度和交通成本的影响。使用雷诺数的基于频率的定义，

其中 $\varphi$ 是驱动频率，$L_{rad}$ 是模型收缩阶段的特征径向位移，$L$ 是钟形直径，$\mu$ 是流体的动态粘度。我们将其用于我们的模型，$L_{rad}/L=0.32$。 $Re$ 固定在250，这是在游泳的水母，特别是月亮水母中发现的 $Re$ 的范围内 (Colin & Costello 2002; Feitl et al. 2009) 。请注意，我们使用基于频率的雷诺数，因此 $Re$ 是取决于前向游泳速度的输入而不是输出。

2.4 运输成本和斯特劳哈尔数

  运输成本(COT)是衡量每一单位行驶距离所花费的能量，对每一种贝尔模型进行了量化。COT经常被用来衡量游泳的效率 (Schmidt-Nielsen 1972; Videler 1993; Bale et al. 2014) 。COT由以下定义

式中，$\overrightarrow{\epsilon }$是整个推进周期内的平均能量，$D^{top}$是整个推进周期内喇叭顶部的垂直位移。这里$\overrightarrow{\epsilon }=|D^{rad}|T$，其中$D^{rad}$是边缘的径向位移，$T$ 是主动张力，并由肌肉激活面积归一化。$T$ 和$D^{rad}$在钟形边缘上进行空间平均，这里定义为未变形构型中 $Z\le 0.08$ 的区域。
  无量纲的Strouhal数是

其中 $D_{max}^{rad}$ 为最大径向位移，$U_{avg}^{top}$ 为第八推进周期内的平均前进速度。游泳和飞行动物通常具有 $0.2<St<0.4$ 的最大推进效率 (Taylor，Nudds&Thomas 2003)。

2.5 模型参数的无量纲化

  钟的材料参数使用特征长度 $L$ 和时间 $\hat{t}$ 进行无量纲化。我们选择 $L=0.125m$ ，这是 Aurelia 的钟的直径，在成年水母的直径范围内。这里 $\hat{t}=1s$ ，大约是主动收缩的持续时间。特征尺寸弹性模量 ${\eta }^D=150kg{m}^{-1}{S}^{-2}$通过以下方法无量纲化

  施加张力的量纲最大值，$T_{max}^D=300kgm{S}^{-2}$，通过以下方法无量纲化

弹性模量的范围选择在水母中胶层和合成中胶层材料的报告值范围内，这些材料用于开发受水母启发的水下航行器 (Demont & Gosline 1988a; Megill et al. 2005; Gambini et al.
2012; Joshi et al. 2013)。

2.6 软件实现

  使用IBAMR实施数值模型，IBAMR是IB方法的分布式内存并行实施，包括笛卡尔网格自适应网格细化(AMR) (IBAMR 2014) 。IBAMR依赖于几个开源库，包括SAMRAI (Hornung，Wissink & Kohn 2006；SAMRAI 2007) 、PETSc (Balay et al. 1997、2009) 、hypre (falgo ut & Yang 2002；HYPRE 2011) 和libMesh (Kirk et al. 2006)。计算区域为长度为8L的立方体，具有周期性边界条件，并使用自适应精细网格进行离散化，其最终笛卡尔网格间距为 $h=8L/512$。无量纲时间步长取 $\Delta t=10$。注意，相对于钟形直径的相对磁畴尺寸是 $8L\times 8L\times 8L$。大的区域尺寸导致模型水母和施加在计算区域外边界上的边界条件之间只有很小的相互作用。

表1。钟形模型的无量纲参考参数表。请注意，长度由钟形直径标准化，时间由施加张力的持续时间标准化。更多细节见2.5。选择参考值来近似在 Aurelia 游泳，每个参数在参考状态上下变化，如每个部分中指定的。

今天的文章水母模型_水螅模型立体制作教程分享到此就结束了，感谢您的阅读。