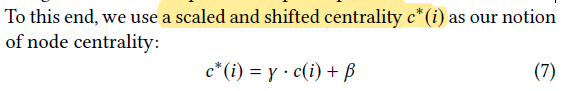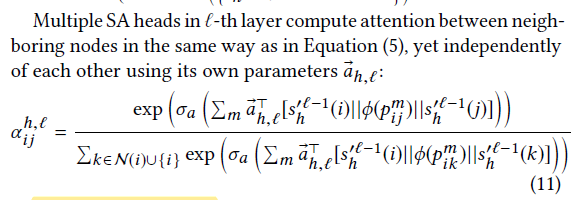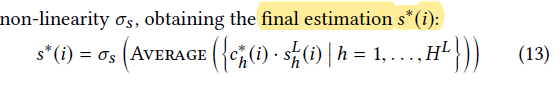GENI: Estimating Node Importance in Knowledge Graphs Using Graph Neural Networks

核心问题：

对于在知识图谱中估计节点重要性的问题，现有方法不能充分利用kg中可用的信息，或者缺乏为实体之间的复杂关系及其重要性建模所需的灵活性。我们提出了一种有监督的机器学习方法，该方法通过谓词感知（即关系）的注意机制和灵活的中心性调整，实现了注意力分数的聚合，而不是节点嵌入的聚合。

挑战包括为相邻节点的重要性之间的关系建模，对不同类型的实体进行准确的估计，并结合先前的节点重要性假设来帮助模型预测。

GENI应用一个注意力的GNN来感知谓词的分数聚合，以捕获节点与其邻居的重要性之间的关系。GENI还允许根据节点中心性灵活调整得分，从而根据图拓扑捕获节点的连通性。

problem definition：

首先定义一个importance score s 表示一个node的重要性/热度（比如一部电影的总票房就可以看作该电影的importance score），这里定义了节点重要性分数的估计：就是给定KG和一些节点的重要性分数，来学习一个function可以预估每个在KG中的节点的importance score。就是通过一个监督框架，学习一个函数，将KG中的任何节点映射到其得分，这样估计就尽可能接近地反映其真正的重要性

这里分为域内和域外估计：域内指的是给定同一类型的分数，估计同一类型的节点分数；域外指的是估计非同一类型的节点分数

对于建模节点重要性的考虑：

 1.Neighborhood Awareness：由于相邻实体之间相互作用，而且它们往往具有共同的特征(网络同质性)，因此在建模节点重要性时应考虑邻域。

2. Make use of predicates(即边/关系）: kg由多种类型的谓词组成。假设不同的谓词在确定节点重要性方面可以发挥不同的作用，模型应该使用来自谓词的信息进行预测

3.centrality Awareness 中心感知：在没有任何其他信息的情况下，有理由认为高度中心的节点比较少中心的节点更重要。因此，需要根据节点的中心性来估算得分，从而获取节点的连通性。

4. 利用input importance score: 除了图拓扑之外，输入重要性得分还提供了有价值的信息来推断节点之间的关系及其重要性。因此，模型应该同时利用图形结构和输入分数来进行更准确的预测。

5. Flexible Adaptive: 我们对于节点重要性的假设，比如中心性的假设，可能与输入分数在kg上的真实分布不一致。此外，我们没有将模型限制在特定类型的输入分数上。另一方面，模型可以提供具有不同特征的输入分数。因此，一个模型能够灵活地适应输入分数所反映的重要性是至关重要的。

具体实现：

作为一种监督学习方法，GNN框架自然允许我们利用输入重要性分数来训练具有灵活适应性的模型（即解决了4，5）。一个实体的表示可以用它的邻居的表示来达到更好地表示，所以我们采用聚合来自邻居的重要性得分来达到（1）的效果。我们设计了谓词感知的注意机制，该机制模拟了谓词如何影响连接实体的重要性（2）；我们采用中心性调整将节点中心性纳入估计（3）

 Score Aggregation：

为了建模节点之间重要性的关系，不像以往那样聚合节点的embedding而是选择聚合节点的重要性分数（importance score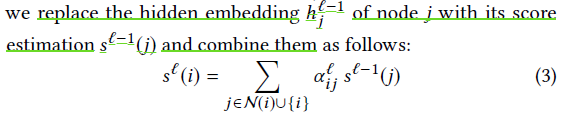）,是一个在节点i，j之间的权重，通过一个注意力机制来学习得到；这里没有transform函数，因为是重要性分数的聚合。初始化输入为节点的feature vector，然后送入任何一个神经网络都可以，这里使用全连接层

 Predicate-Aware Attention Mechanism

 我们采用了一种谓词感知的注意机制来关注邻居的重要性得分：：首先，我们考虑节点之间的谓词，因为不同的谓词可以在得分传播中扮演不同的角色。其次，我们考虑相邻的分数本身来决定注意力。

GENI通过共享谓词嵌入将谓词合并到注意计算中;也就是说，每个谓词由一个预定义长度的特征向量表示，并且该表示由所有层的节点共享。我们用pm- i j表示节点i和节点j之间的第m条边的谓词，
其中表示从谓词到其embedding的映射。

 Centrality Adjustment

常见假设节点的重要性与其在图中的中心性正相关，所以认为更中心的节点将比其他节点更重要，除非给定的重要性分数提供了矛盾的证据

我们定义节点的度为中心度和欢迎度的代替：

我们需要灵活地考虑在给定KG中节点的中心性与提供的节点输入重要性评分之间可能存在的差异,所以考虑到一个缩放和移动的节点中心度表示：（是可学习的缩放参数，是可学习的移动参数）

最后结合中心度和节点传播中最后一层的重要性得分进行非先行转换就得到了final score表示如下

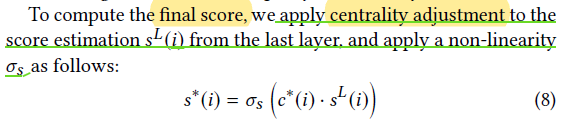
 Model Architecture

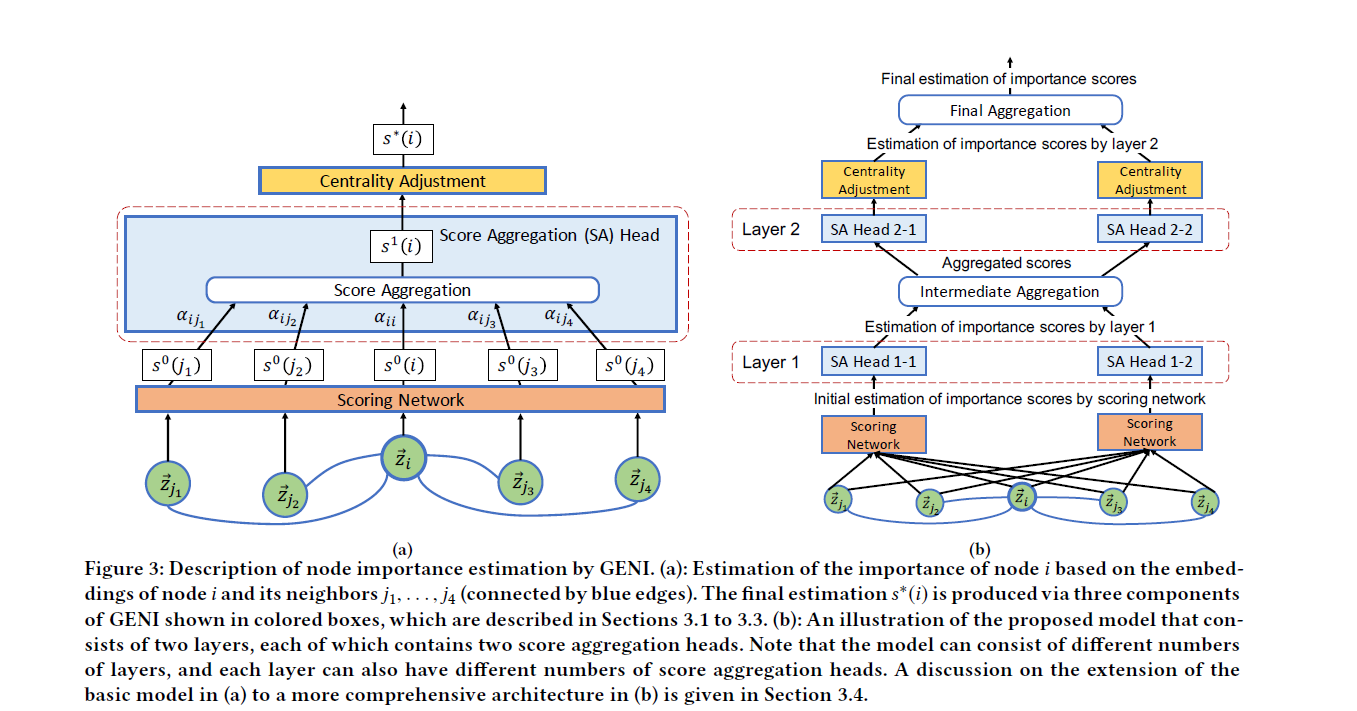
 图3(a)中描述的简单体系结构包括一个评分网络和一个单一评分聚合(SA)层(即，L = 1)，然后是一个中心性调整组件。图3(b)以两种方式将其扩展为更通用的体系结构。

首先，我们对框架进行扩展，使其包含多个SA层;也就是L > 1。作为一个单独的SA层对直接邻居的得分进行聚合，但以多个堆叠SA层允许聚合来自更大邻居的分数。

其次，我们设计每个SA层包含一个可变数量的SA头，这些头各自独立地进行分数聚合和注意力计算。根据经验，我们发现使用多个SA头有助于模型的性能和优化过程的稳定性

对于每层的第h个SA头计算其聚合分数：

对于第一个SA层。每个SA头直接将score作为输入，对于每一层拥有H个SA头最后使用average函数得到该层的聚合表示：

对于每一层每一个头的注意力计算如前述，且拥有自己的单独的参数：

中心性调整实现在最终SA层的输出，为了实现独立的缩放和转移，每个头拥有单独的参数

然后在最后的第L层中，我们拥有H个SA头的情况下进行中心度调整，然后采用average平均，进行非线性转换后得到最终的重要性得分：

 Model training

 使用的是均方差：

今天的文章GENI: Estimating Node Importance in Knowledge Graphs Using Graph Neural Networks分享到此就结束了，感谢您的阅读。