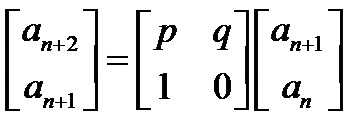特征根法_特征根法和不动点法的原理

之前归纳了一波数列，这里补充一个用于求形如 $a_n=p{a}_{n-1}+q{a}_{n-2}$ 的通项的方法。

（上面这样的递推式可被称作“二阶线性齐次常系数递推式”的特殊情况）

例题

有一数列 { a n } \{a_{n}\} {
an​}，$a_1=x$，$a_2=y$，且 $\forall n\ge 3$，都有 $a_n=p{a}_{n-1}+q{a}_{n-2}$。求该数列的通项公式。

解

不难想象这种线性递推式的答案都是指数形式的。
我们知道一阶线性递推式推出来一定会有一个指数项。那二阶递推式出来是不是会有两个指数项呢？

答案是肯定的，递推式一定能表示为 $a_n=c_1{r}_1^{n-1}+c_2{r}_2^{n-1}$。这里给结论给的比较突兀，严格证明限于编者能力暂时没法给出 ，但是读者可以想象：对递推式的两个项不断迭代，一个迭代到 $a_1$，一个迭代到 $a_2$，这样这两个项一定齐次，且次数与 $n$ 同阶。

现在问题就是求描述中的常数。我们利用类似待定系数的思想先将该式代入递推式：

$c_1{r}_1^n+c_2{r}_2^n=p{c}_1{r}_1^{n-1}+p{c}_2{r}_2^{n-1}+q{c}_1{r}_1^{n-2}+q{c}_2{r}_2^{n-2}$

$c_1{r}_1^{n-2}(r_1^2-p{r}_1-q)+c_2{r}_2^{n-2}(r_2^2-p{r}_2-q)=0$ 、

要使原式成立，必然要求

$r_1^2-p{r}_1-q=0$ 且 $r_2^2-p{r}_2-q=0$，即 $r_1、r_2$ 为方程 $x^2-px-q=0$
的两根。

我们把上述方程称作原递推式的 特征方程 。

然后我们又有 $a_1=c_1+c_2=x$，$a_2=c_1{r}_1+c_2{r}_2=y$，

此时 $r_1、r_2$ 已知，所以 $c_1、c_2$ 可求，这样我们就求完了。

补充说明

我们可以从矩阵的观点来看，由递推式子我们可以得到转移矩阵：

（图片来自 http://tieba.baidu.com/p/3820580861 @lgy_hello_life，侵权请联系笔者删除）
这个矩阵的特征多项式¹即为 $x^2=px+q$。

今天的文章特征根法_特征根法和不动点法的原理分享到此就结束了，感谢您的阅读。