sin函数微分公式_高斯函数积分公式

（三）中对SINS的机械编排进行了初步可行性的介绍，并未对机械编排进行原理性介绍。那么在详细介绍机械编排之前，需要先对SINS的微分方程进行详细的推导。

无论是机械编排，还是后面误差方程的建立，SINS的微分方程都是其重要的基础内容。那么本文在基于严恭敏《惯性导航》的基础上，对SINS中常见的微分方程进行推导。

（二）中对INS常用的坐标系统及转换进行了介绍，同时介绍了姿态的三种表示方法，以及三种方法之间的相互转换。

1. 姿态的三种表示方法

• 欧拉角法
  欧拉角法对应于载体坐标系的三个旋转角（roll， pitch， yaw）
• 方向余弦矩阵法
  方向余弦矩阵（DCM）又被称为“坐标变换矩阵”，用于将矢量投影从一个坐标系变换到另一个坐标系中。
• 四元素法
  四元数法是指有一个实数单位1和三个虚数单位i，j，k组成并具有如下形式实元的数。

下面对姿态微分方程的推导是也是基于这三种方法进行推导。

2. 姿态微分方程推导

欧拉角微分方程

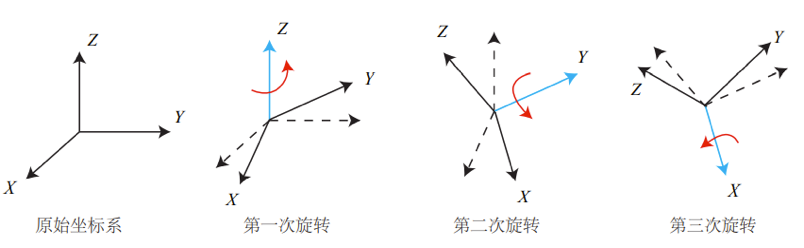
欧拉角的旋转方式有很多种，常用的是ZYX旋转。这里的旋转指的是欧拉角的定义方式上的旋转。如下图所示，即为ZYX旋转。

上面三次旋转都对应一个坐标转换矩阵，这里分别为$R_{\psi }$、$R_{\theta }$、$R_{\varphi }$。其具体形式不在这里给出，感兴趣的可以自行搜索。

欧拉角微分方程的推导就对应着上面三次旋转。
1）第一次旋转
绕原始坐标系Z轴旋转产生$\psi$角，产生的旋转角速度在旋转后的临时坐标系1中的表示是绕Z轴方向，因此在1系中的表示为：$${\hat{\omega }}_1=\left[\begin{array}{c}0\\ 0\\ \dot{\psi }\end{array}\right]$$
2）第二次旋转
绕中间坐标系1系Y轴旋转$\theta$角，产生的旋转角速度在旋转后的临时坐标系2中的表示也是绕Y轴方向， 因此在2系中很好表示，但是旋转也改变了第一次旋转角速度的表示。因此前两次旋转在2系中的表示为：$${\hat{\omega }}_2=\left[\begin{array}{c}0\\ \dot{\theta }\\ 0\end{array}\right]+R_{\theta }{\hat{\omega }}_1=\left[\begin{array}{c}-\dot{\psi }sin\theta \\ \dot{\theta }\\ \dot{\psi }cos\theta \end{array}\right]$$
3）第三次旋转
绕中间坐标系2系的X轴旋转$\varphi$角，产生的旋转角速度在旋转后的最终坐标系中的表示也是绕X轴方向，但是同样改变了前两次旋转角速度的表示，三次旋转在最终坐标系中的表示为：$${\hat{\omega }}_b=\left[\begin{array}{c}\dot{\varphi }\\ 0\\ 0\end{array}\right]+R_{\varphi }{\hat{\omega }}_2=\left[\begin{array}{ccc}1& 0& -sin\theta \\ 0& cos\varphi & sin\varphi cos\theta \\ 0& -sin\varphi & cos\varphi cos\theta \end{array}\right]\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$
即$${\hat{\omega }}_b=\left[\begin{array}{ccc}1& 0& -sin\theta \\ 0& cos\varphi & sin\varphi cos\theta \\ 0& -sin\varphi & cos\varphi cos\theta \end{array}\right]\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$
其中$${\hat{\omega }}_b=\left[\begin{array}{c}{\omega }_{nb,x}^b\\ {\omega }_{nb,y}^b\\ {\omega }_{nb,z}^b\end{array}\right]$$
对矩阵求逆即可得到欧拉角微分方程。欧拉角微分方程在惯导和组合导航中用的不多。
方向余弦矩阵微分方程
欧拉角和DCM之间是可以相互转换的。上述欧拉角三次旋转是对应的旋转矩阵相乘就是DCM。即$$R_n^b=R_{\psi }\cdot R_{\theta }\cdot R_{\varphi }=\left[\begin{array}{ccc}cos\theta cos\psi & -cos\varphi sin\psi +sin\varphi sin\theta cos\psi & sin\varphi sin\psi +cos\varphi sin\theta cos\psi \\ cos\theta sin\psi & cos\psi cos\varphi +sin\psi sin\theta sin\varphi & -cos\psi sin\varphi +sin\psi sin\theta cos\varphi \\ -sin\theta & sin\varphi cos\theta & cos\theta cos\varphi \end{array}\right]$$
当三个欧拉角为小角度的时候，由极限知识可得：$$R_y^x=\left[\begin{array}{ccc}1& -{\psi }_{xy}& {\theta }_{xy}\\ {\psi }_{xy}& 1& -{\varphi }_{xy}\\ -{\theta }_{xy}& {\varphi }_{xy}& 1\end{array}\right]=I+(v\times ),v=\left[\begin{array}{c}{\varphi }_{xy}\\ {\theta }_{xy}\\ {\psi }_{xy}\end{array}\right]$$
另外，需要注意的是转置存在如下关系：
$$C_{b(t_k)}^{b(t_j)}=I-(\Delta {\theta }_{b(t_k)b(t_j)}\times ),C_{b(t_j)}^{b(t_k)}=I+(\Delta {\theta }_{b(t_k)b(t_j)}\times )$$
（1）设r为空间向量，由哥氏定理：
$$\frac{dr}{dt}{|}_n=\frac{dr}{dt}{|}_b+{\omega }_{nb}\times r$$
（2）上式向b系投影：
$$\frac{dr}{dt}{|}_n^b=\frac{dr}{dt}{|}_b^b+({\omega }_{nb}\times r{)}^b$$
（3）由于：
$$\frac{dr}{dt}{|}_b^b={\dot{r}}^b$$
$$({\omega }_{nb}\times r{)}^b={\omega }_{nb}^b\times r^b$$
（4）代入到（2）式得：
$${\dot{r}}^b=\frac{dr}{dt}{|}_n^b-{\omega }_{nb}^b\times r^b$$
（5）由于$r^b=C_n^b{r}^n$，对其两边求导：
$${\dot{r}}^b={\dot{C}}_n^b{r}^n+c_n^b{\dot{r}}^n={\dot{C}}_n^b{r}^n+C_n^b\frac{dr}{dt}{|}_n^n$$
（6）上式中$C_n^b\frac{dr}{dt}{|}_n^n$即位$\frac{dr}{dt}{|}_n^b$，所以上式变为：
$${\dot{r}}^b={\dot{C}}_n^b{r}^n+\frac{dr}{dt}{|}_n^b$$
（7）式与（4）式对比可得：
$${\dot{C}}_n^b=-{\omega }_{nb}^b\times r^b=-{\omega }_{nb}^b\times C_n^b{r}^n=-{\omega }_{nb}^{bk}{C}_n^b{r}^n$$
（8）最终得：
$${\dot{C}}_n^b=-{\omega }_{nb}^{bk}{C}_n^b$$
转置得：
$${\dot{C}}_b^n=C_b^n{\omega }_{nb}^{bk}$$
其中，${\omega }_{nb}^{bk}$为旋转欧拉角向量的反对称矩阵。
四元素微分方程
（1）定义b系到n系的四元素为Q，则用欧拉角表示为
$$Q=cos\frac{\theta }{2}+{\mu }^{R}sin\frac{\theta }{2}$$
（2）对上式两边求导：
$$\frac{dQ}{dt}=-\frac{\dot{\theta }}{2}sin\frac{\theta }{2}+{\mu }^R\frac{\dot{\theta }}{2}cos\frac{\theta }{2}+sin\frac{\theta }{2}\frac{d{\mu }^R}{dt}$$
（3）由哥氏定理：
$$\frac{d{\mu }^R}{dt}=C_b^R\frac{d{\mu }^b}{dt}+{\omega }_{Rb}^R\times {\mu }^R$$
（4）其中：$\frac{d{\mu }^b}{dt}=0$，且${\omega }_{Rb}^R=\dot{\theta }{\mu }^R$,故$\frac{d{\mu }^R}{dt}=0$
（5）则（2）式变为：
$$\frac{dQ}{dt}=-\frac{\dot{\theta }}{2}sin\frac{\theta }{2}+{\mu }^R\frac{\dot{\theta }}{2}cos\frac{\theta }{2}$$
（6）对（1）式两边乘$\frac{\dot{\theta }}{2}{\mu }^R$得：
$$\frac{\dot{\theta }}{2}{\mu }^R\otimes Q=\frac{\dot{\theta }}{2}{\mu }^R\otimes (cos\frac{\theta }{2}+{\mu }^{R}sin\frac{\theta }{2})=\frac{\dot{\theta }}{2}{\mu }^{R}cos\frac{\theta }{2}+{\mu }^R\otimes {\mu }^{R}sin\frac{\theta }{2}=\frac{\dot{\theta }}{2}{\mu }^{R}cos\frac{\theta }{2}-sin\frac{\theta }{2}$$
（7） 则（5）与（6）相比即有：
$$\frac{dQ}{dt}=\frac{\dot{\theta }}{2}{\mu }^R\otimes Q=\frac{1}{2}{\omega }_{Rb}^R\otimes Q=\frac{1}{2}Q\otimes {\omega }_{Rb}^b=\frac{1}{2}WQ$$
上式即为四元素微分方程。其中w为欧拉角向量的反对称矩阵。
速度微分方程

• 地速：$\frac{dr}{dt}{|}_e=ve$
• 哥氏方程：$\frac{dr}{dt}{|}_a={\frac{dr}{dt}}_b+{\omega }_{ab}\times r$
• 导航方程：$\frac{d^{2}r}{d{t}^2}{|}_i=f+g$

（1）由哥氏方程和地速定义（i 系）：
$$\frac{dr}{dt}{|}_i=\frac{dr}{dt}{|}_e+{\omega }_{ie}\times r=v_e+{\omega }_{ie}\times r$$
（2）在i系下求导：
$$\frac{d^{2}r}{d{t}^2}=\frac{d{v}_e}{dt}{|}_i+\frac{d}{dt}({\omega }_{ie}\times r){|}_i$$
（3）利用导航方程整理可得：
$$\frac{d{v}_e}{dt}{|}_i=f+g-\frac{d{\omega }_{ie}}{dt}{|}_i\times r-{\omega }_{ie}\times \frac{dr}{dt}{|}_i=f+g-{\omega }_{ie}\times (v_e+{\omega }_{ie}\times r)=f-{\omega }_{ie}\times v_e+(g-{\omega }_{ie}\times ({\omega }_{ie}\times r))=f-{\omega }_{ie}\times v_e+g_l$$
投影到i系：
$$=C_b^i{f}^b-{\omega }_{ie}^i\times v_e^i+g_l^i$$
上式即为速度微分方程。
位置微分方程
在INS中位置是由速度确定，因此其微分方方程也较为简单，在各种书籍论文中常用的位置微分方程如下所示：
$${\dot{r}}^n=\left[\begin{array}{c}\dot{\varphi }\\ \dot{\lambda }\\ \dot{h}\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R_M+h}& 0& 0\\ 0& \frac{1}{(R_N+h)cos\varphi }& 0\\ 0& 0& -1\end{array}\right]\left[\begin{array}{c}{v}_N\\ v_E\\ v_D\end{array}\right]=D^{-1}{v}^n$$

今天的文章sin函数微分公式_高斯函数积分公式分享到此就结束了，感谢您的阅读。