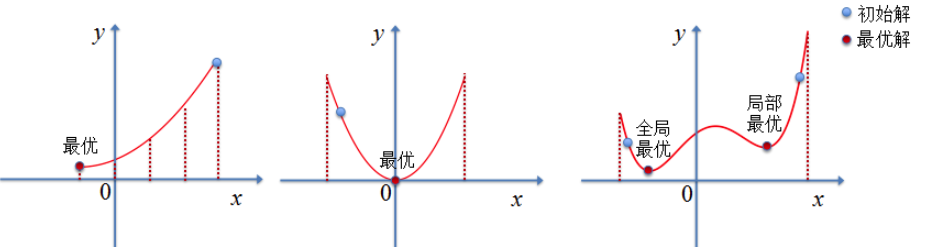
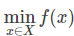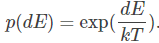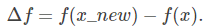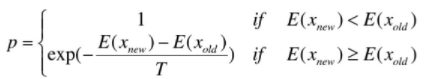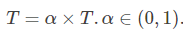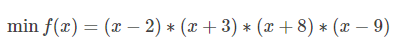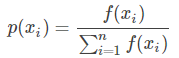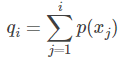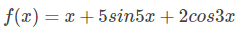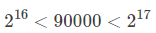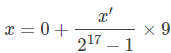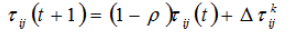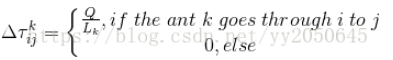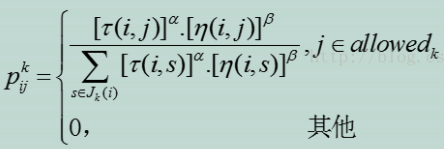如下问题:在某个给定的定义域X内,求函数f(x)对应的最优值。此处以最小值问题举例,形式化为:
如果 X是离散有限取值,那么可以通过穷取法获得问题的最优解;如果X连续,但f(x)是凸的,那可以通过梯度下降等方法获得最优解;如果X连续且f(x)非凸,虽说根据已有的近似求解法能够找到问题解,可解是否是最优的还有待考量,很多时候若初始值选择的不好,非常容易陷入局部最优值。
第三种问题经常遇见。如何有效地避免局部最优的困扰?模拟退火算法应运而生。其实模拟退火也算是启发式算法的一种,具体学习的是冶金学中金属加热-冷却的过程。
模拟退火算法到底是如何模拟金属退火的原理?主要是将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。
演算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。若概率大于给定的阈值,则跳转到“邻居”;若概率较小,则停留在原位置不动。
一、模拟退火算法基本思想
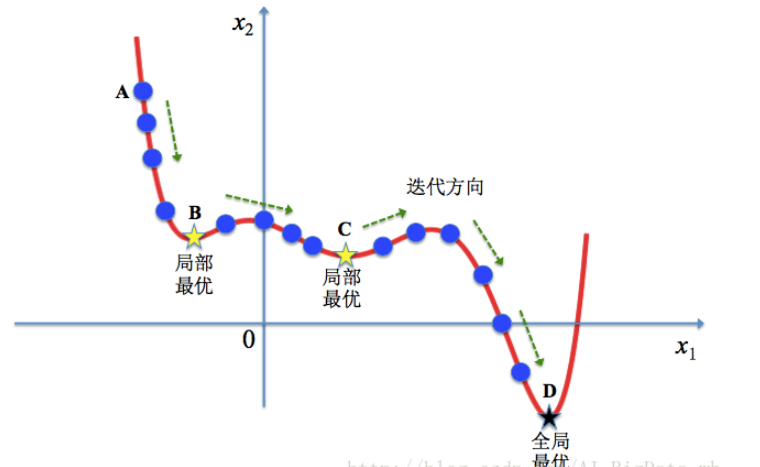
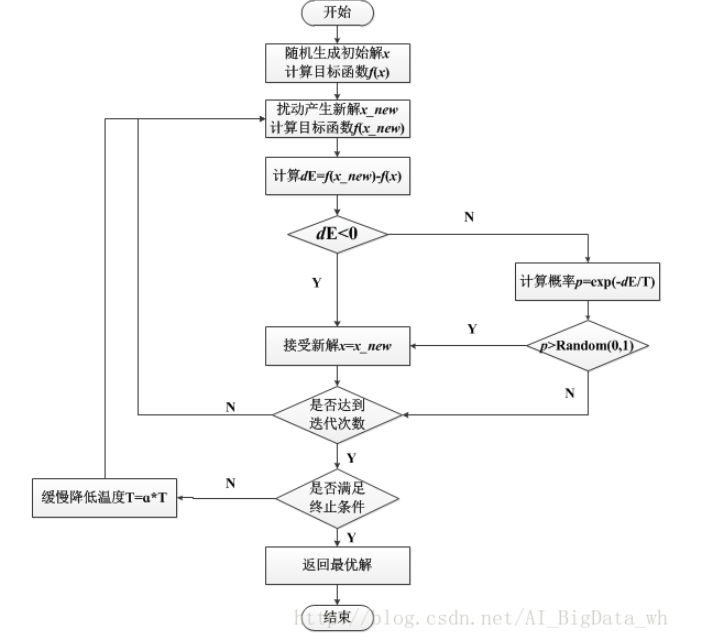
想象一下如果我们现在有下面这样一个函数,以下图为例,现在想求函数的(全局)最优解。如果使用梯度下降法,假定初始解为左边蓝色点A,那么从A点开始试探,如果函数值继续减少,那么试探过程就会继续。而当到达点B时,显然我们的探求过程就结束了(因为无论朝哪个方向努力,结果只会越来越大)。最终我们只能找到一个局部最后解B。
模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。在迭代更新可行解时,以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。对于下图,模拟退火算法会快速搜索到局部最优解B,但在搜索到局部最优解后,不是就此结束,而是会以一定的概率接受到右边的移动。也许经过几次这样的不是局部最优的移动后会到达全局最优点D,于是就跳出了局部最小值。
根据热力学的原理,在温度为T时,出现能量差为dE的降温的概率为p(dE),表示为:
其中k是波尔兹曼常数,值为
在实际问题中,这里的“一定的概率”的计算参考了金属冶炼的退火过程。假定当前可行解为xx,迭代更新后的解为x_new,那么对应的“能量差”定义为:
常表示为:
上式表明,在温度为T时,出现能量差为dE的降温的概率为P(dE),且dE<0。所以P和T正相关。又由于dE总是小于0(因为退火的过程是温度逐渐下降的过程),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。也就是说,在用固体退火模拟组合优化问题,将内能E模拟为目标函数值 f,温度T演化成控制参数 t,即得到解组合优化问题的模拟退火演算法:由初始解 i 和控制参数初值 t 开始,对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代,并逐步衰减 t 值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。
总结:
- 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解),则总是接受该移动;
- 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差),则以一定的概率接受移动,而且这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)相当于上图中,从B移向BC之间的小波峰时,每次右移(即接受一个更糟糕值)的概率在逐渐降低。如果这个坡特别长,那么很有可能最终我们并不会翻过这个坡。如果它不太长,这很有可能会翻过它,这取决于衰减 t 值的设定。
二、模拟退火算法描述
三、模拟退火算法的优缺点
模拟退火算法的应用很广泛,可以高效地求解NP完全问题,但其参数难以控制,不能保证一次就收敛到最优值,一般需要多次尝试才能获得(大部分情况下还是会陷入局部最优值)。主要存在如下三个参数问题:
(1) 温度T的初始值设置问题
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。
(2) 每个T值的迭代次数
模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说,同一温度下的“充分”搜索是相当必要的,但这也需要计算时间。循环次数增加必定带来计算开销的增大。
(3) 温度管理问题
温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下所示的降温方式:
注:为了保证较大的搜索空间,α一般取接近于1的值,如0.95、0.9
from:模拟退火与遗传与蚁群算法
from:模拟退火与遗传与蚁群算法
经过上面理论知识的熏陶,相信大家已经对模拟退火算法有了较深入的理解,接下来通过实战再强化一下大家的认识,此处利用模拟退火算法求解如下优化问题:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def inputfun(x):
return (x-2)*(x+3)*(x+8)*(x-9)
initT = 1000 #初始温度
minT = 1 #温度下限
iterL = 1000 #每个T值的迭代次数
delta = 0.95 #温度衰减系数
k = 1
initx = 10*(2*np.random.rand()-1)
nowt = initT
print "初始解:",initx
xx = np.linspace(-10,10,300)
yy = inputfun(xx)
plt.figure()
plt.plot(xx,yy)
plt.plot(initx,inputfun(initx),'o')
#模拟退火算法寻找最小值过程
while nowt>minT:
for i in np.arange(1,iterL,1): #每个T值迭代1000次
funVal = inputfun(initx)
xnew = initx+(2*np.random.rand()-1)
if xnew>=-10 and xnew<=10:
funnew = inputfun(xnew)
res = funnew-funVal
if res<0: #新的结果更好
initx = xnew
else:
p = np.exp(-(res)/(k*nowt))
if np.random.rand()<p:
initx = xnew
nowt = nowt*delta #迭代完1000次,降低温度
print "最优解:",initx
print "最优值:",inputfun(initx)
plt.plot(initx,inputfun(initx),'*r')
plt.show()1、遗传算法简介
遗传算法是一种基于自然选择和群体遗传机理的搜索算法,它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象。
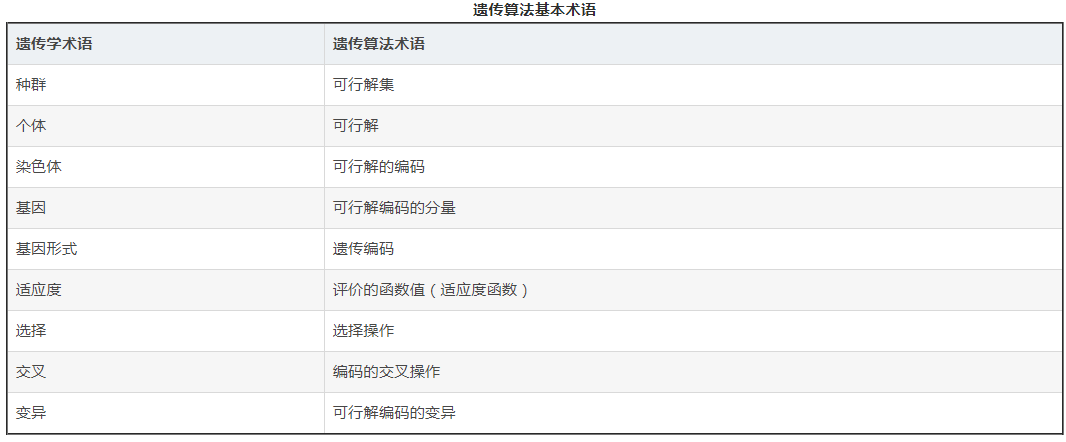
遗传算法的概念简单来说,就是利用种群搜索技术将种群作为一组问题解,通过对当前种群施加类似生物遗传环境因素的选择、交叉、变异等一系列的遗传操作来产生新一代的种群,并逐步使种群优化到包含近似最优解的状态。
在利用遗传算法求解问题时,问题的每一个可能解都被编码成一个“染色体”,即个体,若干个个体构成了群体(所有可能解)。在遗传算法开始时,总是随机的产生一个种群(即初始解),根据预定的目标函数对种群中每一个个体进行评估,给出一个适应度值,基于此适应度值,选择一些个体用来产生下一代,选择操作体现了“适者生存”的原理,“好”的个体被用来产生下一代,“坏”的个体则被淘汰,然后选择出来的个体,经过交叉和变异算子进行再组合生成新的一代,这一代的个体由于继承了上一代的一些优良性状,因而在性能上要优于上一代,这样逐步朝着最优解的方向进化.因此,遗传算法可以看成是一个由可行解组成的群体初步进化的过程.
编码
利用遗传算法求解问题时,首先要确定问题的目标函数和变量,然后对变量进行编码,这样做主要是因为在遗传算法中,问题的解是用数字串来表示的,而且遗传算子也是直接对串进行操作的。一个问题的一个可行解即被称为一条“染色体”。一个可行解一般由多个元素构成,那么这每一个元素就被称为染色体上的一个“基因”。
2、适应度函数
在遗传算法中,如何衡量染色体的优劣呢?这就是由适应度函数完成的。它能够选择出每一代中比较优良的个体,而淘汰一些环境适应度较差的个体。
遗传算法在运行的过程中会进行N次迭代,每次迭代都会生成若干条染色体。适应度函数会给本次迭代中生成的所有染色体打个分,来评判这些染色体的适应度,然后将适应度较低的染色体淘汰掉,只保留适应度较高的染色体,从而经过若干次迭代后染色体的质量将越来越优良。
3、遗传操作
遗传操作的任务就是根据个体适应度对其施加一定的操作,从优化搜索的角度来看,遗传操作可以使问题的解逐代优化,逼近最优解,遗传操作包括以下三个基本遗传算子:选择、交叉、变异。选择和交叉基本上完成了遗传算法的大部分搜索功能,变异增加了遗传算法找到最优解的能力.
3.1、选择
选择是指从群体中选择优良个体并淘汰劣质个体的操作.它建立在适应度评估的基础上.适应度越大的个体,被选中上的可能性就越大,他的“子孙”在下一代中的个数就越多,选择出来的个体就被放入配对库中.目前常用的选择方法有轮赌盘方法、最佳个体保留法、期望值法、排序选择法.
轮盘赌选择
又称比例选择方法.其基本思想是:各个个体被选中的概率与其适应度大小成正比.
具体操作如下:
(1)计算出群体中每个个体的适应度f(i=1,2,…,n),n为群体大小;
(2)计算出每个个体被遗传到下一代群体中的概率;
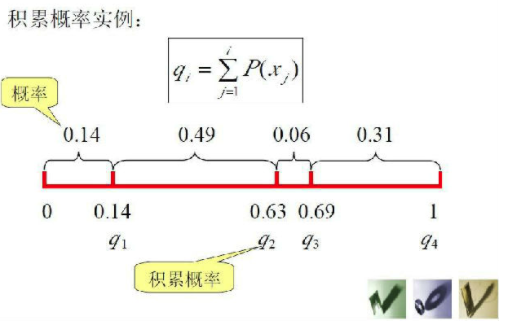
(3)计算出每个个体的累积概率;
(q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率)
(4)在[0,1]区间内产生一个均匀分布的伪随机数r;
(5)若r<q[1],则选择个体1,如果q[k-1]<r≤q[k] 成立,选择个体k;
(6)重复(4)、(5)共n次,则选出n个个体。
def selection(population,value):
#轮盘赌选择
fitness_sum=[]
for i in range(len(value)):
if i ==0:
fitness_sum.append(value[i])
else:
fitness_sum.append(fitness_sum[i-1]+value[i])
for i in range(len(fitness_sum)):
fitness_sum[i]/=sum(value)
#select new population
population_new=[]
for i in range(len(value)):
rand=np.random.uniform(0,1)
for j in range(len(value)):
if j==0:
if 0<rand and rand<=fitness_sum[j]:
population_new.append(population[j])
else:
if fitness_sum[j-1]<rand and rand<=fitness_sum[j]:
population_new.append(population[j])
return population_new3.2、交叉
交叉就是指把两个父代个体的部分结构加以替换重组而生成新的个体的操作,交叉的目的是为了在下一代产生新的个体,通过交叉操作,遗传算法的搜索能力得到了飞跃性的提高.交叉是遗传算法获取优良个体的重要手段。交叉操作是按照一定的交叉概率在匹配库中随机的选取两个个体进行的,交叉位置也是随机的,交叉概率一般取得很大,为0.6~0.9.
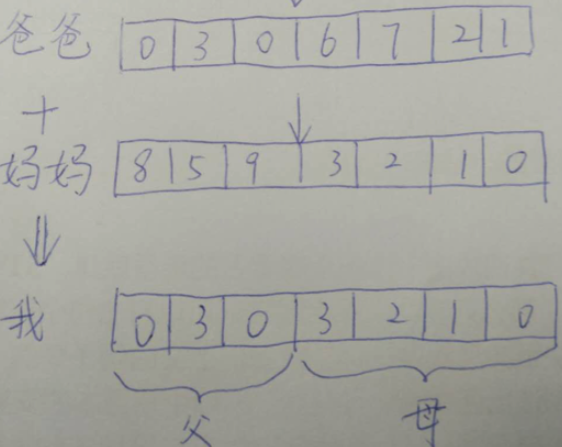
那么,如何从上一代染色体中选出爸爸和妈妈的基因呢?这不是随机选择的,一般是通过轮盘赌算法完成。
在每完成一次进化后,都要计算每一条染色体的适应度,然后计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。
"""
crossover.py
"""
from __future__ import division
import numpy as np
def crossover(population_new, pc):
half=int(len(population_new)/2)
father=population_new[:half]
mother=population_new[half:]
np.random.shuffle(father)
np.random.shuffle(mother)
offspring=[]
for i in range(half):
if np.random.uniform(0,1)<=pc:
copint = np.random.randint(0,int(len(father[i])/2))
son=father[i][:copint]+(mother[i][copint:])
daughter=mother[i][:copint]+(father[i][copint:])
else:
son=father[i]
daughter=mother[i]
offspring.append(son)
offspring.append(daughter)
return offspring
3.3、变异
变异就是以很小的变异概率Pm随机地改变种群中个体的某些基因的值,变异操作的基本过程是:产生一个[0,1]之间的随机数rand,如果rand<Pm,则进行变异操作。变异操作本身是一种局部随机搜索,与选择、交叉算子结合在一起,能够避免由于选择和交叉算子而引起的某些信息永久性丢失,保证了遗传算法的有效性,使遗传算法具有了局部随机搜索能力,同时使得遗传算法能够保持群体的多样性,以防出现未成熟收敛.在变异操作中,变异概率不宜取得过大,如果Pm>0.5,遗传算法就退化为了随机搜索.
def mutation(offspring,pm): #对交叉后的子样本变异
for i in range(len(offspring)):
if np.random.uniform(0,1)<=pm:
position=np.random.randint(0,len(offspring[i]))
#'str' object does not support item assignment,cannot use = to change value
if position!=0:
if offspring[i][position]=='1':
offspring[i]=offspring[i][:position-1]+'0'+offspring[i][position:]#字符串是不可变量,不能直接修改,所以使用这种方法重新初始化offspring
else:
offspring[i]=offspring[i][:position-1]+'1'+offspring[i][position:]
else:
if offspring[i][position]=='1':
offspring[i]='0'+offspring[i][1:]
else:
offspring[i]='1'+offspring[i][1:]
return offspring3.4、复制
每次进化中,为了保留上一代优良的染色体,需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。假设每次进化都需生成N条染色体,那么每次进化中,通过交叉方式需要生成N-M条染色体,剩余的M条染色体通过复制上一代适应度最高的M条染色体而来。
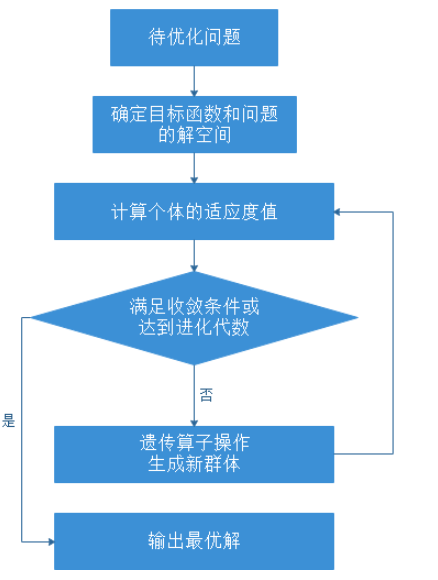
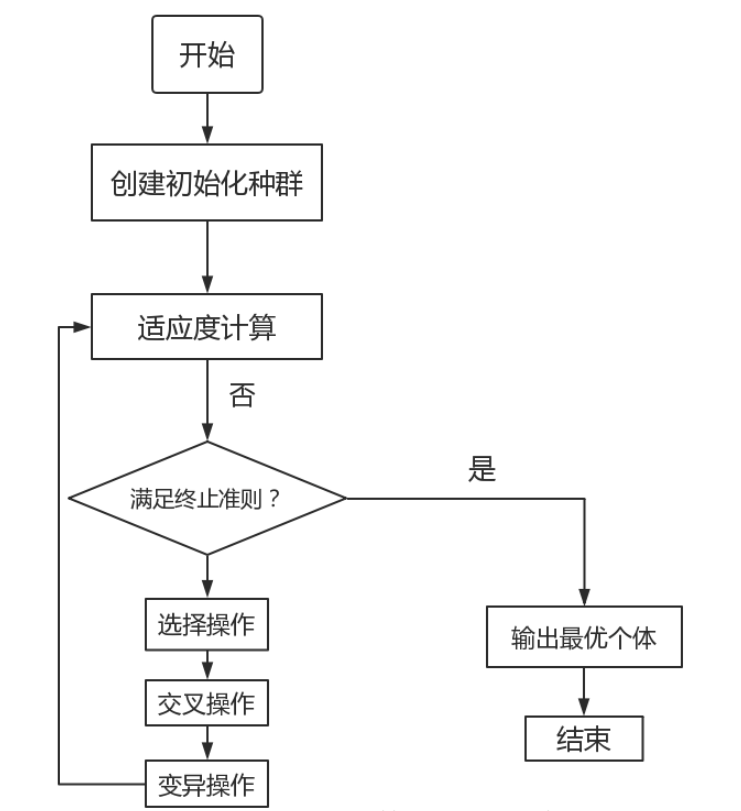
遗传算法的流程图
from:模拟退火与遗传与蚁群算法
from:模拟退火与遗传与蚁群算法
from:模拟退火与遗传与蚁群算法
需要求这个函数在[0,9]的最大值并需要精确到4位小数。同样,如果使用穷举法,需要计算90000次。现在我们来看看如何用遗传算法优化求解过程。
1、编码与解码(code and decode)
实行遗传算法的首要任务是要确定编码与解码的形式,基本遗传算法(SGA)都是选取二进制编码。对于上面的问题,我们考虑90000个数将自变量空间划分成了90000个等份,现在使用二进制来表示这90000个等份,由于:
那么,只需要17为二进制字符串便可以表达每一个等份,每一等份都对应一个不同的字符串。现在,如何将二进制字符串转化回原自变量呢?首先将二进制转化为十进制,然后归一化到【0,9】:
如00000000000000000便代表0,而11111111111111111代表9。确定了编码与解码的方式,我们现在可以随机产生一群个体作为我们的初始种群。
"""
Genetic Algorithm
"""
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
import math
def aimFunction(x):
y=x+5*math.sin(5*x)+2*math.cos(3*x)
return y
x=[i/100 for i in range(900)]
y=[0 for i in range(900)]
for i in range(900):
y[i]=aimFunction(x[i])初始化一个种群,注意population是字符串列表
population=[]
for i in range(10):
entity=''
for j in range(17):
entity=entity+str(np.random.randint(0,2))
population.append(entity)解码,适应度函数
def decode(x):
y=0+int(x,2)/(2**17-1)*9
return y
def fitness(population,aimFunction):
value=[]
for i in range(len(population)):
value.append(aimFunction(decode(population[i])))
#weed out negative value
if value[i]<0:
value[i]=0
return value关于int(x,[base]): base代表着参照的进制,base>=2,(base也可取0,此时和base取10一样)
比如int(’20’,8),代表的就是八进制的‘20’,也就是‘16’,int强转后就输出整型的16
然后定义三个算子,首先是选择,交叉,变异:参见:模拟退火与遗传与蚁群算法
定义完所有算子后,我们便可以开始进化过程了,定义进化次数为1000次,交叉概率为0.7,变异概率为0.02:
t=[]
for i in range(1000):
#selection
value=utils.fitness(population,aimFunction)
population_new=selection(population,value)
#crossover
offspring =crossover(population_new,0.7)
#mutation
population=mutation(offspring,0.02)
result=[]
for j in range(len(population)):
result.append(aimFunction(utils.decode(population[j])))
t.append(max(result))蚁群算法,也是优化算法当中的一种。蚁群算法擅长解决组合优化问题。蚁群算法能够有效的解决著名的旅行商问题(TSP)
蚁群算法,顾名思义就是根据蚁群觅食行为而得来的一种算法。单只蚂蚁的觅食行为貌似是杂乱无章的,但是据昆虫学家观察,蚁群在觅食时总能够找到离食物最近的路线,经过研究发现,每一只蚂蚁在觅食的过程中,会在沿途释放出一种叫做信息素的物质。其他蚂蚁会察觉到这种物质,因此,这种物质会影响到其他蚂蚁的觅食行为。当一些路径上经过的蚂蚁越多时,这条路径上的信息素浓度也就越高,其他蚂蚁选择这条路径的可能性也就越大,从而更增加了这条路径上的信息素浓度。当然,一条路径上的信息素浓度也会随着时间的流逝而降低。这种选择过程被称之为蚂蚁的自催化行为,是一种正反馈机制,也可以将整个蚁群认定为一个增强型学习系统。
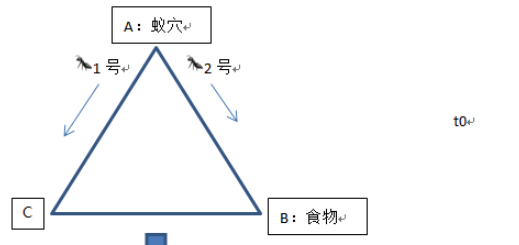
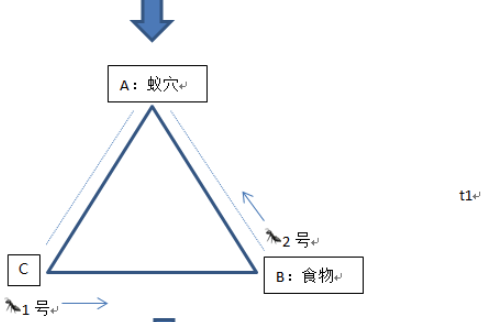
如图所示,A点为一个蚁穴,设定其中有两只蚂蚁,蚂蚁1和蚂蚁2。B点为食物所在位置,C点只是路径上的一点。假设ABC形成一个等边三角形,且两只蚂蚁的移动速度均相同。在t0时刻,两只蚂蚁在蚁穴中,在他们面前有两条路可以选择,即AB或AC。两只蚂蚁随机进行选择,我们假设蚂蚁1选择了路径AC,而蚂蚁2选择了路径AB。
在t1时刻是,蚂蚁1走到了C点,而蚂蚁2走到了B点,即食物所在位置。他们在其经过的路径上释放了信息素,在途中用虚线表示。之后蚂蚁2将食物运往蚁穴,并依然在沿途释放信息素,蚂蚁1则从C点向B点进发。
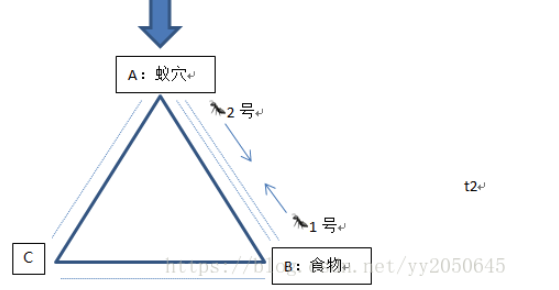
等到t2时刻时,蚂蚁2到达了蚁穴A点,蚂蚁1到达了食物所在位置B点,此时蚂蚁2再次出发去搬运食物,它发现AB路径上的信息素浓度要高于AC路径上的信息素浓度(AB路径上有两条虚线,AC路径上只有1条虚线)。因此蚂蚁2选择AB路径去搬运食物,而蚂蚁1则在B点获取到了食物,接下来返回蚁穴,但是它也有两种选择,一种是原路返回,另一种便是走线路AB。蚂蚁1发现AB路径上的信息素浓度要高于AC路径上的信息素浓度,因此它将选择AB来返回蚁穴。
如此往复,AC路径的信息素浓度会越来越低,AB路径上的信息素浓度会越来越高,所以AC路径上将没有蚂蚁再次经过,两只蚂蚁都只会选择路径较短的AB线路去搬运食物。
以TSP问题为例来进行说明。
TSP(Traveling Salesman Problem):什么是TSP问题,TSP问题及著名的旅行商问题。这个问题简单描述就是:假设一个旅行商人,他要遍历n个城市,但是每个城市只能遍历一次,最终还要回到最初所在的城市,要求制定一个遍历方案,使经过的总路程最短。
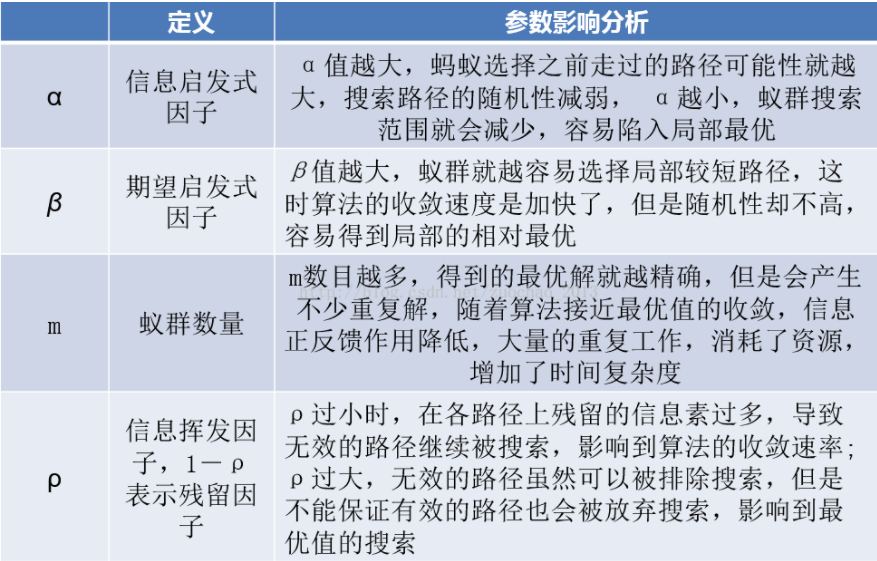
接下来便用蚁群算法对这个问题进行求解,首先列出一些蚁群算法中涉及到的参数及其符号:
m:蚂蚁数量,约为城市数量的1.5倍。如果蚂蚁数量过大,则每条路径上的信息素浓度趋于平均,正反馈作用减弱,从而导致收敛速度减慢;如果过小,则可能导致一些从未搜索过的路径信息素浓度减小为0,导致过早收敛,解的全局最优性降低





n:城市数量

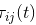
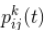
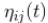
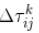
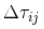
蚁群算法的基本步骤:
1、蚂蚁在路径上释放信息素。
2、碰到还没走过的路口,就随机挑选一条路走。同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时,就选择信息素浓度较高路径。
4、最优路径上的信息素浓度越来越大。
5、最终蚁群找到最优寻食路径
每次周游,每只蚂蚁在其经过的支路(i,j)上都留下信息素,蚂蚁选择城市的概率与(城市之间的距离和当前连接支路上所包含的信息素余量有关)。为了强制蚂蚁进行合法的周游,直到一次周游完成后,才允许蚂蚁游走已访问过的城市(这可由禁忌表来控制)。
基本蚁群的两个过程:
(1)信息素更新
为了避免残留信息素过多而淹没启发信息,在每只蚂蚁走完一步或者完成对所有n个城市的遍历(也即一个循环结束)后,要对残留信息进行更新处理。
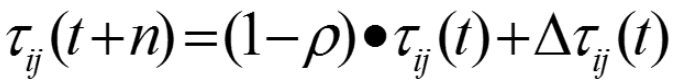
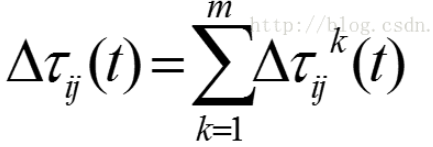
这个公式反映了信息素浓度的迭代更新规律,可以看出,所有蚂蚁遍历完一次所有城市后,当前信息素浓度由两部分组成,第一部分即上次所有蚂蚁遍历完所有城市后路径上信息素的残留,第二部分为本次所有蚂蚁遍历完所有城市后每条路径上的信息素的新增量。
反映了每只蚂蚁对于自己经过的城市之间路径上信息素浓度的贡献量,可以看出,其经历的路程越长,则对于沿途上信息素浓度的贡献量也就越低,如果尽力的路程越短,则对于沿途上信息素浓度的贡献量也就越高,
(2)状态转移
从公式中可以看出信息素因子
from:模拟退火与遗传与蚁群算法
from:模拟退火与遗传与蚁群算法
今天的文章模拟退火和蚁群算法_遗传算法和蚁群算法哪个简单分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/89188.html