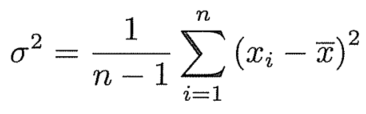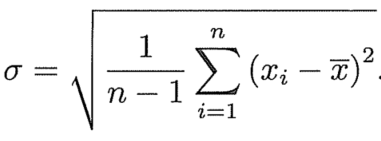描述性统计的概念_描述性统计SPSS分析

1. 书籍和文中所提到的数据会在文末提供百度云下载，所有数据都不会有加密，可以放心下载使用

2. 文中计算的结果与书中不同是由于数据使用的时间段不同

目录

1. 准备数据

2. 绘制频数直方图

 3. 数据的位置

4. 数据的离散度

1. 准备数据

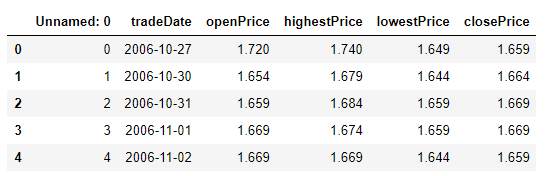
原始数据 600000.csv 600050.csv 601398.csv 三个文件里是收盘价，通过收盘价计算日收益率

import pandas as pd
# 中国工商银行   ICBC   601398
# 浦发银行  SPDB  600000
# 中国联通  ChinaUnicom  600050
df_601398 = pd.read_csv('./601398.csv',encoding='utf-8')
df_600000 = pd.read_csv('./600000.csv',encoding='utf-8')
df_600050 = pd.read_csv('./600050.csv',encoding='utf-8')
df_601398.head()

df_601398['o_date'] = df_601398['tradeDate']
df_601398['o_date'] = pd.to_datetime(df_601398['o_date'])
df_601398.sort_values(by='o_date',ascending=True,inplace=True)
# daily_returns 日收益率
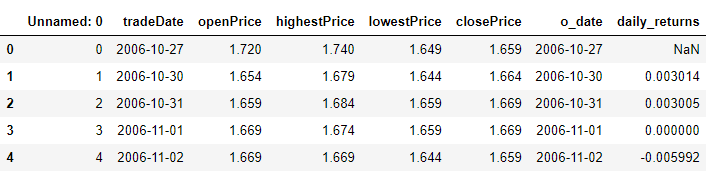
df_601398['daily_returns'] = (df_601398['closePrice']-df_601398['closePrice'].shift(1))/df_601398['closePrice'].shift(1)
df_601398.head()

df_600000['o_date'] = df_600000['tradeDate']
df_600000['o_date'] = pd.to_datetime(df_600000['o_date'])
df_600000.sort_values(by='o_date',ascending=True,inplace=True)
df_600000['daily_returns'] = (df_600000['closePrice']-df_600000['closePrice'].shift(1))/df_600000['closePrice'].shift(1)

df_600050['o_date'] = df_600050['tradeDate']
df_600050['o_date'] = pd.to_datetime(df_600050['o_date'])
df_600050.sort_values(by='o_date',ascending=True,inplace=True)
df_600050['daily_returns'] = (df_600050['closePrice']-df_600050['closePrice'].shift(1))/df_600050['closePrice'].shift(1)

# 中国工商银行  gsyh
df_601398.rename(columns={'daily_returns':'gsyh'},inplace=True)
# 浦发银行  pfyh
df_600000.rename(columns={'daily_returns':'pfyh'},inplace=True)
# 中国联通 zglt
df_600050.rename(columns={'daily_returns':'zglt'},inplace=True)

df_601398 = df_601398.loc[:,['tradeDate','gsyh']]
df_600000 = df_600000.loc[:,['tradeDate','pfyh']]
df_600050 = df_600050.loc[:,['tradeDate','zglt']]

合并到一个表中，按日期对齐

three_df = pd.merge(df_601398,df_600000,how='inner',on='tradeDate')
three_df = pd.merge(three_df,df_600050,how='inner',on='tradeDate')
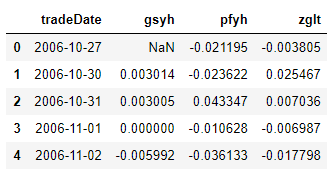
three_df.head()

three_df.to_csv('chapter_13_dailyreturns.csv',encoding='utf-8')

2. 绘制频数直方图

import matplotlib.pyplot as plt
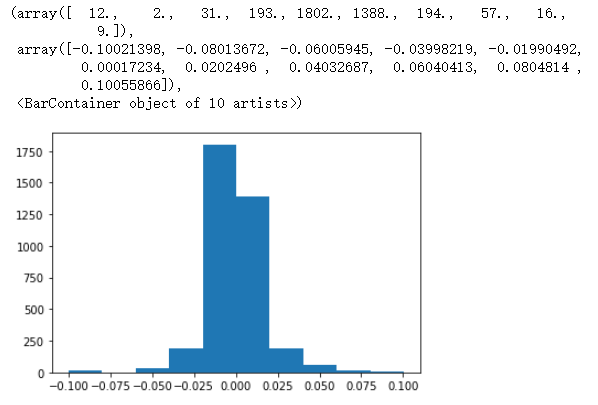
# 频数直方图
gsyh = three_df.gsyh
plt.hist(gsyh)

 3. 数据的位置

概念：

样本平均数(Sample Mean)、中位数(Median)、众数(Mode)、百分位数(Percentile)

# 平均数
three_df.zglt.mean()
# out: 0.0004284562650822751

# 中位数
three_df.zglt.median()
# out: 0.0

# 众数
three_df.zglt.mode()
# out:0    0.0
#     dtype: float64

# 上下四分位数
[three_df.zglt.quantile(i) for i in [0.25,0.75]]
# out: [-0.010317115551694248, 0.010245151847786325]

4. 数据的离散度

概念:

4.1 极差(Range)

4.2 平均绝对偏差(Mean Absolute Deviation)

4.3 方差(Variance) 和标准差(Standard Deviation)

方差公式:

 标准差公式:

# 极差
three_df.zglt.max()-three_df.zglt.min()
# out: 0.2016438874062682

# 平均绝对偏差
three_df.zglt.mad()
# out: 0.015984757661984345

# 方差
three_df.zglt.var()
# out: 0.0005796109187107064

# 标准差
three_df.zglt.std()
# out: 0.024075109941819713

PS:

链接：https://pan.baidu.com/s/1Jck5WqDunfyph18UvguJ5g 
提取码：5fo3

书籍

链接：https://pan.baidu.com/s/1xJD85-LuaA9z-Jy_LU5nOw 
提取码：ihsg

今天的文章描述性统计的概念_描述性统计SPSS分析分享到此就结束了，感谢您的阅读。