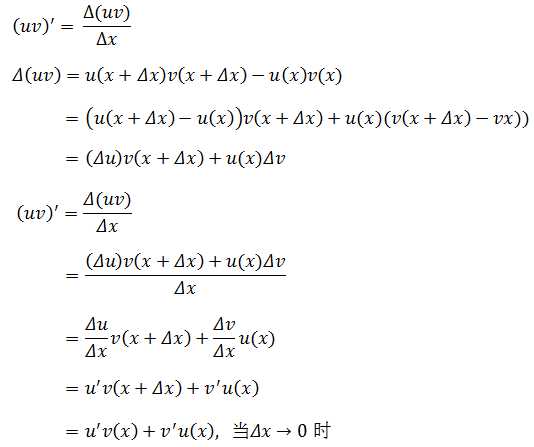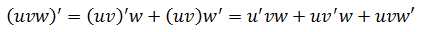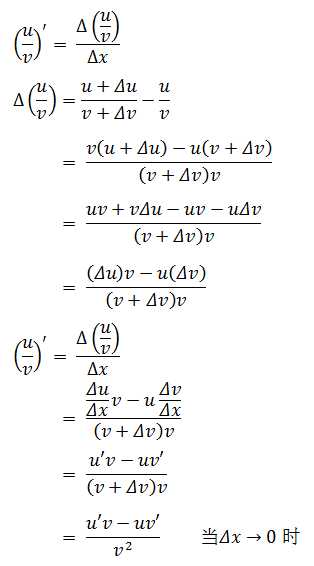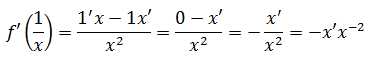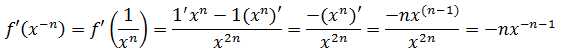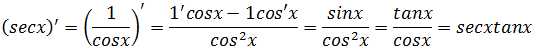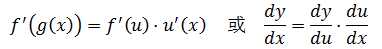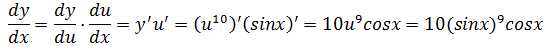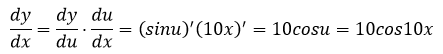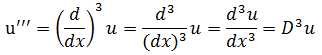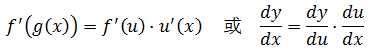导数及高阶导数的计算方法_常用高阶导数公式

和、差、积、商求导法则

　　设u=u(x),v=v(x)都可导，则：

1. (Cu)’ = Cu’, C是常数
2. (u ± v)’ = u’ ± v’
3. (uv)’ = u’v + uv’
4. (u/v)’ = (u’v – uv’) / v2

　　1、2不解释，下面给出3、4的推导过程

乘法法则的推导过程

　　乘法法则可扩展：

除法法则的推导过程

示例1：f'(1/x)

　　根据除法法则：

示例2：f'(x-n)

　　根据除法法则：

　　上式结果也可直接根据幂函数求导法则得出，幂函数f(x) = Xn的导数：f’(x) = nxn-1

示例3：（secx）’

链式求导法则

　　链式求导法则也称为复合函数求导法则。若u=g(x)在x点可导，y=f(u)在u=g(x)点可导，则y=f(g(x))在x点可导，其导数是：

　　第二种写法看起来更好理解。

示例1：y=(sinx)10求导

　　这是一个典型的符合函数，内部函数是u=sinx，外部函数是y=u10，根据公式：

示例2：sin(10x)求导

高阶导数

　　高阶导数实际上是对导数求导，也就是不断求导。

　　二阶导数表示为(u’)’=u’’；三阶导数u’’’；四阶导数不能再用撇号表示了，需要使用上标u(4)；n阶导数u(n)。在训练集中，上标也被表示为第几组训练集，在此我们看到，数学中的符号经常会被重用，在不同上下文中有不同的含义。

　　sinx的二阶导数：(sinx)’’=(cosx)’=-sinx

　　高阶导数也有不同的表示法，以三阶导数为例：

　　看起来越来越乱了-_-|||

幂函数的高阶导数

D1xn = nxn-1

D2xn = ( D1xn)’= (nxn-1)’=n(xn-1)’=n(n-1)(x n-2)

D3xn = (D2xn)’ = n(n-1)(n-2)(xn-3)

……

Dn-1xn = n(n-1)(n-2)(n-3)…(2)x1

Dnxn = n(n-1)(n-2)(n-3)…(2)(1)x0 = n!

Dn+1xn = (n!)’ = 0

高阶导数的意义

　　几何意义比较容易理解，一阶导数是切线的斜率，二阶是斜率的变化率，三阶是斜率的变化率的变化率……阶数越高，刻画的变化越精细。

　　物理意义是百度来的，用时间、距离、速度举例：

　　位移相对于时间的一阶导数是速度，二阶导数是加速度，三阶导数是急动度(加速度的的变化率)，四阶导数是什么痉挛度(不知道是不是瞎编出来的，从这开始就理解不了了)……当一辆小车尾部遭受撞击时，加速度会突然改变，小车具有急动度。汽车工程师用急动度作为评判乘客不舒适程度的指标；按照这一指标,具有恒定加速度和零急动度的人体感觉最舒适。在竞技举重中，举重运动员进行所有将杠铃举过头顶的动作时都有急动度。当轮船到达溪谷，突然减速时，轮船有急动度，因为轮船加速度的大小和方向都要改变。

总结

　　1.函数的和、差、积、商求导法则

　　1)         (Cu)’ = Cu’, C是常数

　　2)         (u ± v)’ = u’ ± v’

　　3)         (uv)’ = u’v+ uv’

　　4)         (u/v)’ = (u’v – uv’) / v2

　　2.链式求导法则（复合函数求导法则）

　　3.高阶导数

　　对导数求导，u’’,u’’’,u(4)

　　Dnxn = n!

　　Dn+1xn = 0

    作者：我是8位的

   出处：http://www.cnblogs.com/bigmonkey

   本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

今天的文章导数及高阶导数的计算方法_常用高阶导数公式分享到此就结束了，感谢您的阅读。