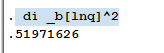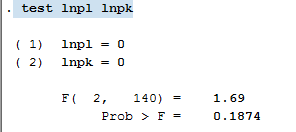一、线性回归基本命令

regress y x1 x2   （红色表示该命令可简写为红色部分）

以 Nerlove 数据为例（数据附后文）

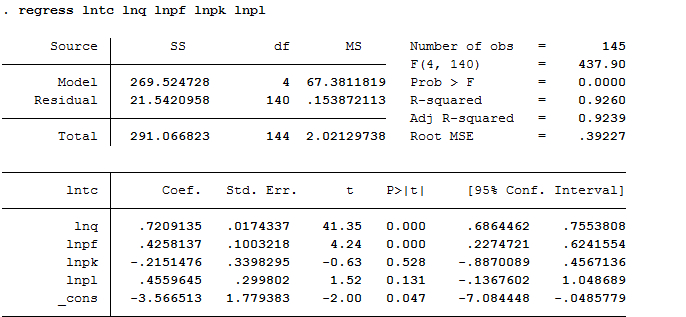
regress lntc lnq lnpf lnpk lnpl

      表上半部分为方差分析表，包括回归平方和，残差平方和，均方，F检验等。上半部分右侧给出拟合优度R2和调整的R2。root MSE 表示方程的标准误差。

    表下半部分为回归系数的点估计和区间估计值，标准误和t检验值。

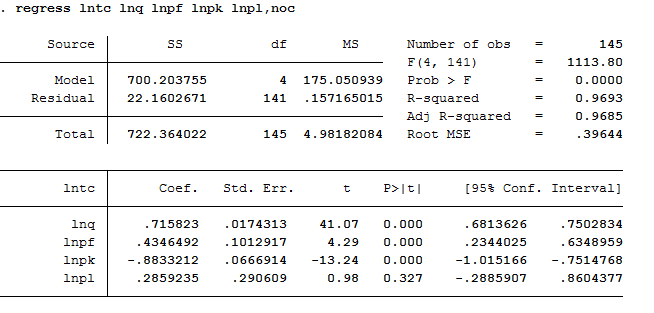
如果回归不需要常数项，则可在命令后面加上 noconstant

regress lntc lnq lnpf lnpk lnpl,noc

二、带约束条件的回归

如果只对满足一定条件的样本进行回归，可增加条件项  if 条件

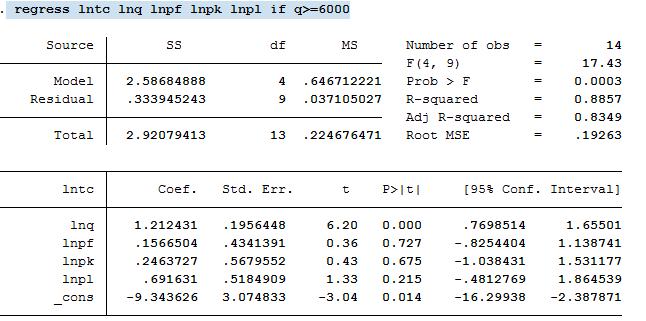
假如本例中q>=6000认定为大企业，则可设置如下命令

 regress lntc lnq lnpf lnpk lnpl if q>=6000

或者使用虚拟变量表示，定义一个新变量large ,如果是大企业，则取值为1，否则为0，代码为

 g large=(q>=6000)

 regress lntc lnq lnpf lnpk lnpl if large

输出结果等价于上面if条件结果。

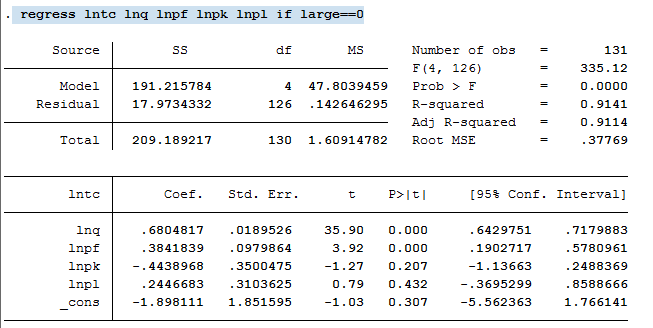
如果对非大企业进行回归，则可表示为

 regress lntc lnq lnpf lnpk lnpl if large==0

如果回归系数需满足某些指定条件，比如a1+a2+a3=1,a1=2a2 等，则可通过设置约束条件完成：

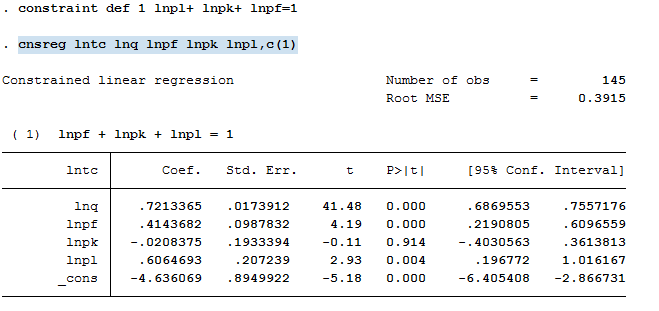
 constraint def 1 lnpl+ lnpk+ lnpf=1
 
 cnsreg lntc lnq lnpf lnpk lnpl,c(1)

constraint def  1  定义第一个约束条件，cnsreg表示带约束回归，c(1) 表示满足约束条件1

如果需要同时满足几个条件，可以进一步设置条件2，条件3，以新增约束条件lnq=1 为例

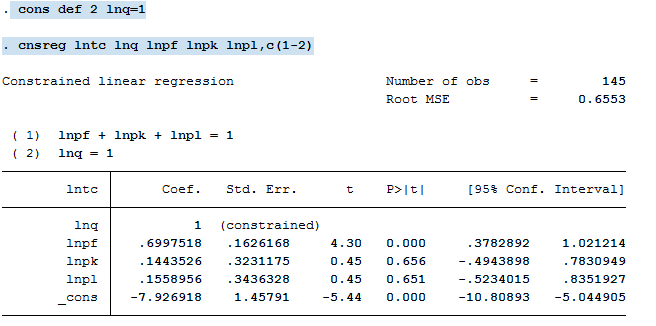
 cons def 2 lnq=1

 cnsreg lntc lnq lnpf lnpk lnpl,c(1-2)

三、预测、检验和相关计算

如果要计算因变量的拟合值，并保存到新变量yhat中，则可采用predict：

以对无约束条件的回归进行预测为例：

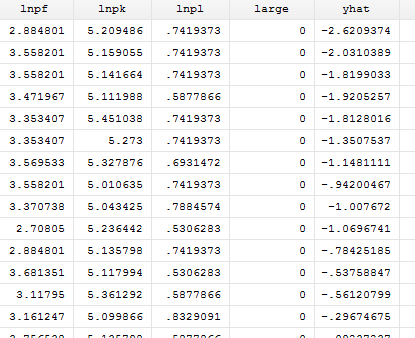
regress lntc lnq lnpf lnpk lnpl

predict yhat

预测结果保存在原始数据集中

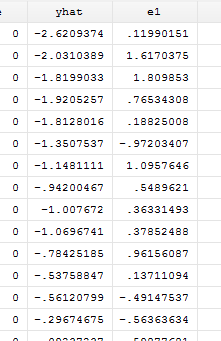
进一步计算残差，并保存到e1中，则可（其中residual可简写）：

 predict e1,residual

残差e1结果保存在原始数据中

如果要对某个系数进行计算，可直接采用display 表达式方式，比如计算lnq的平方

 di _b[lnq]^2

如果需要对系数进行某种条件检验，可采用test 条件，以检验lnq=1，lnpl+lnpk+lnpf=1 为例

 te lnq=1
 te (lnq=1)(lnpl+lnpk+lnpf=1)

单独检验lnq=1，F检验显示拒绝原假设；联合检验lnq=1，lnpl+lnpk+lnpf=1，拒绝联合成立的原假设。

对两个系数同时等于0进行假设，可采用命令 te 变量1 变量2 ，以检验lnpl lnpk联合等于0为例：

 test lnpl lnpk

F检验表明不拒绝两者皆为0的原假设。

今天的文章stata 线性回归分析基本操作分享到此就结束了，感谢您的阅读。