【普通卷积】

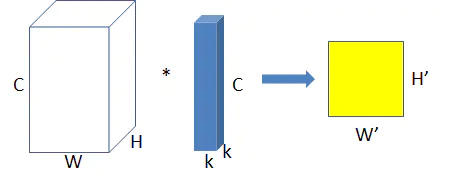
上图为普通卷积示意图，为方便理解，图中只有一个卷积核，此时输入
输出数据为：输入feature map尺寸：$W\times H\times C$ ，分别对应feature map的宽，高，通道数；
单个卷积核尺寸：$k\times k\times C$ ，分别对应单个卷积核的宽，高，通道数；
输出feature map尺寸 ：$W^{\prime }\times H^{\prime }$ ，输出通道数等于卷积核数量，输出的宽和高与卷积步长有关，这里不关心这两个值。

参数量: $params=k^{2}C$
运算量:$FLOPs=k^{2}C{W}^{\prime }{H}^{\prime }$,这里只考虑浮点乘数量，不考虑浮点加。

【group convolution (分组卷积)】

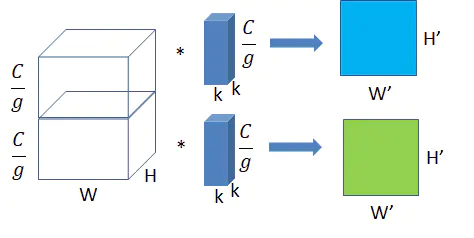
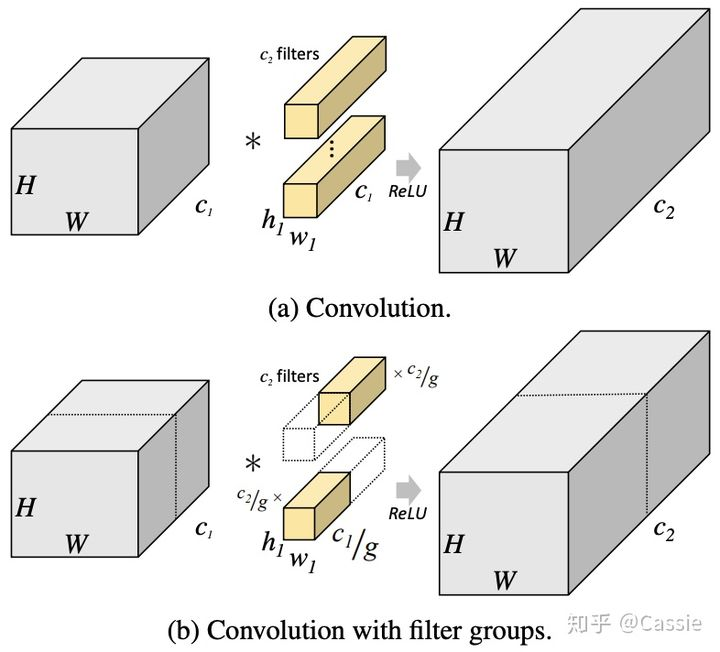
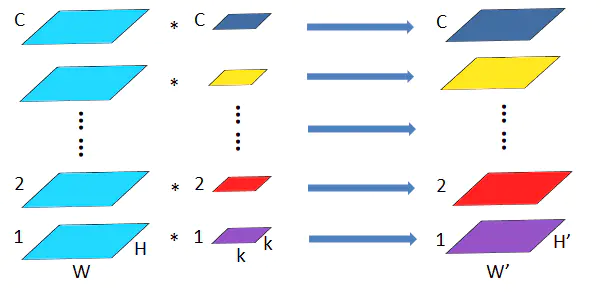
将图一卷积的输入feature map分成组，每个卷积核也相应地分成组，在对应的组内做卷积，如上图2所示，图中分组数，即上面的一组feature map只和上面的一组卷积核做卷积，下面的一组feature map只和下面的一组卷积核做卷积。每组卷积都生成一个feature map，共生成个feature map。

假设input.shape = [$C_1$, H, W] output.shape = [$C_2$, $H^1$, $W^1$]
输入每组feature map尺寸：$W\times H\times \frac{C_1}{g}$ ，共有g组。
单个卷积核每组的尺寸：$k\times k\times \frac{C_2}{g}$，一个卷积核被分成了g组。
输出feature map尺寸：$W^1\times H^1\times g$，共生成g个feature map。
现在我们再来计算一下常规卷积的参数量和运算量：
参数量$params=k\times k\times C_1\times C_2$
运算量$FLOPs=k^2\times C1\times C_2{W}^1\times H^1=k^2{C}_1{C}_2{W}^1{H}^1$
现在我们再来计算一下分组卷积时的参数量和运算量：
参数量$params=k^2\times \frac{C_1}{g}\times \frac{C_2}{g}\times g=k^2\frac{C_1}{g}{C}_2$
运算量$FLOPs=k^2\times \frac{C_1}{g}{C}_2\times W^1\times H^1=k^2\frac{C_1}{g}{C}_2{W}^1{H}^1$
上面的例子我们可以清楚地看到,得到相同的output.shape,分组卷积的参数量是常规卷积的1/g,其中g是分组的个数(上图中是两个)。

• 分析：
  利用分层过滤组提高CNN效率论文地址
  官方分析：Alex认为group conv的方式能够增加 filter之间的对角相关性,而且能够减少训练参数,不容易过拟合,这类似于正则的效果。
• 代码实现(pytorch提供了相关参数,以2d为例)

import torch
import torch.nn as nn
...
model = nn.Conv2d(in_channels = in_channel, out_channels = out_channel, 
kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = group_num)

【深度可分离卷积】

MobileNets:论文地址
深度可分离卷积是MobileNet的精髓,它由deep_wise卷积和point_wise卷积两部分组成。我以前一直觉得深度可分离卷积是极端化的分组卷积(把group数量设为Cin个就行)。但今天再次思考一下,发现他们很大的不同在于,分组卷积只进行一次卷积(一个nn.Conv2d即可实现),不同group的卷积结果concat即可,而深度可分离卷积是进行了两次卷积操作,第一次先进行deep_wise卷积(即收集每一层的特征),kernel_size = KK1,第一次卷积总的参数量为KKCin,第二次是为了得到Cout维度的输出,kernel_size = 11Cin,第二次卷积总的参数量为11Cin*Cout。第二次卷积输出即为深度可分离卷积的输出。
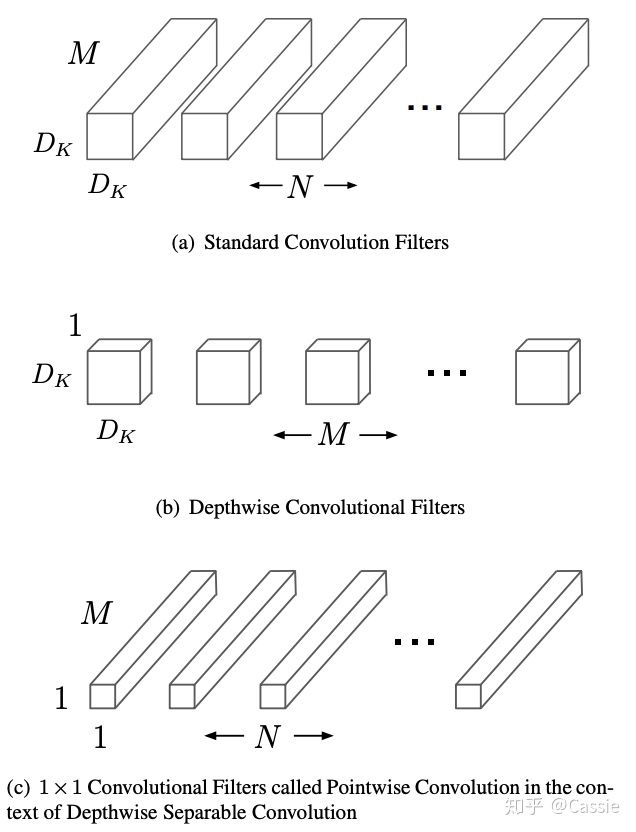
以下就是论文中提到的深度可分离卷积可视化图：

• 举例

举个例子比较参数量：假设input.shape = [$c_1$, H, W] output.shape = [$c_2$, H, W]
(a)常规卷积参数量=$k\times k\times c_1\times c_2$
(b)深度可分离卷积参数量=$k\times k\times c1+1\times 1\times c_1\times c_2$

上面的例子我们可以清楚地看到,得到相同的output.shape,直观看上去,深度可分离卷积的参数量比常规卷积少了一个数量级。

• 分析

深度可分离卷积同时考虑图像的区域和通道(深度可分离卷积首先只考虑区域depth_wise,然后再只考虑通道point_wise)实现了图像的区域和通道的完全分离。

• 代码实现(pytorch)

import torch
import torch.nn as nn
...
model = nn.Sequential(
        nn.Conv2d(in_channels = in_channel, out_channels = in_channel, 
kernel_size = kernel_size, stride = stride, padding = 1, dilation = dilation, group = in_channel),
        nn.Conv2d(in_channels = in_channel, out_channels = out_channel kernel_size = 1, padding = 0)
        )

之所以在写在前面中提到,本文的题目一定要先是分组卷积再是深度可分离卷积,因为在我看来后者是前者的极端情况(分组卷积的group设为in_channel,即每组的channel数量为1),尽管形式上两者有比较大的差别:分组卷积只进行一次卷积操作即可,而深度可分离卷积需要进行两次——先depth_wise再point_wise卷积,但他们本质上是一样的。

深度可分离卷积进行一次卷积是无法达到输出指定维度的tensor的,这是由它将group设为in_channel决定的,输出的tensor通道数只能是in_channel,不能达到要求,所以又用了11的卷积改变最终输出的通道数。这样的想法也是自然而然的,BottleNeck不就是先11卷积减少参数量再33卷积feature map,最后再11恢复原来的通道数,所以BottleNeck的目的就是减少参数量。提到BottleNeck结构就是想说明1*1卷积经常用来改变通道数。

这样,分组卷积和深度可分离卷积就能很好地联系起来并牢牢掌握啦！！！

今天的文章group convolution (分组卷积)详解分享到此就结束了，感谢您的阅读。