有向无环图Directed Acyclic Graph（DAG）

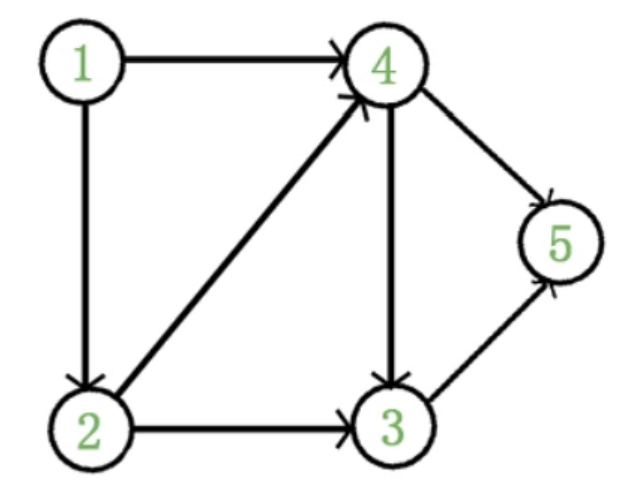
1、DAG

• 有向无环图Directed Acyclic Graph（DAG）
• DAG是一个没有 有向循环的、有限的有向图 。
  1. 它由有限个顶点和有向边组成，每条有向边都从一个顶点指向另一个顶点；
  2. 从任意一个顶点出发都不能通过这些有向边回到原来的顶点。
  3. 有向无环图就是从一个图中的任何一点出发，不管走过多少个分叉路口，都没有回到原来这个 点的可能性。
• 条件
  • 每个顶点出现且只出现一次
  • 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。
• 计算一个DAG的拓扑关系
  1. 1→4表示4的入度+1，4是1的邻接点
  2. 首先将边与边的关系确定，建立好入度表和邻接表。
  3. 从入度为0的点开始删除，如上图显然是1的入度为0，先删除。
  4. 判断有无环的方法，对入度数组遍历，如果有的点入度不为0，则表明有环。
  5. { 1, 2, 4, 3, 5 }

今天的文章有向无环图Directed Acyclic Graph（DAG）分享到此就结束了，感谢您的阅读。