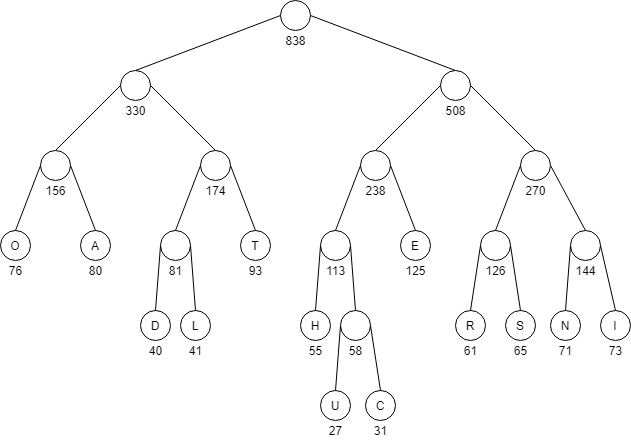
一问题描述

用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。给出现频率高的字符较短的编码，出现频率较低的字符以较长的编码，贪心算法使平均码长达到最小的前缀码编码方案。
输入：字符集C和每一字符的频率。
输出：每一字符的编码。

二算法基本思路

编码字符集C中每一字符c的频率是f(c)。
以f为键值的优先队列Q用在贪心选择时确定算法当前要合并的两棵具有最小频率的树。
一旦两棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的两棵树的频率之和，并将新树插入优先队列Q。
经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。
伪代码：

HUFFMAN(C)
	n = |C|
	Q = C
	for i=1 to n-1
	allocate a new node z
	z.left = x =EXTRACT-MIN(Q)
	z.right = y =EXTRACT-MIN(Q)
	z.freq = x.freq + y.freq
	INSERT(Q,z)
	return EXTRACT-MIN(Q)

三算法复杂性分析

时间复杂度：O(nlogn)
假定Q是使用最小二叉堆实现的，对一个n个字符的集合C，在第2行用BUILD-MIN-HEAP过程将Q初始化，花费时间为O(n)。第3~8行的for循环执行了n-1次，且每个堆操作需要O(logn)的时间，所以循环对总时间的贡献为O(nlogn)。
空间复杂度：O(n)

四 C++代码

#include <iostream>
#include <string.h>
using namespace std;
// Huffman编码：T(n) = O(nlogn)

typedef struct{ 
   
    unsigned int weight; // 结点权重
    unsigned int parent,lchild,rchild; // 父节点、左右孩子
    char character; // 字符
}HTNode,*HuffmanTree; // 动态分配数组存储Huffman树

typedef char **HuffmanCode; // 动态分配数组存储Huffman编码表

// 在所有结点中选择权值最小的2个结点s1、s2
void Select(HuffmanTree HT, int n, int &s1, int &s2){ 
   
    if(n<2) return;
   int w1=-1,w2=-1;
    for(int i=1;i<=n;i++){ 
   
        if(HT[i].parent==0){ 
   
            if(w1==-1||HT[i].weight<=w1){ 
   
                w1=HT[i].weight;
                s1=i;
            }
        }
    }
    for(int i=1;i<=n;i++){ 
   
        if(HT[i].parent==0&&i!=s1){ 
   
            if(w2==-1||HT[i].weight<=w2&&HT[i].weight>=w1){ 
   
                w2=HT[i].weight;
                s2=i;
            }
        }
    }
}

// Huffman编码
// w存放n个字符的权值（均>0），构造Huffman树HT，并求出n个字符的Huffman编码HC
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, char *&character, int n){ 
   
    if(n<=1) return;
    int m=2*n-1;
    HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 构造Huffman树，0号单元未用
    HuffmanTree p;
    int i;
    for(p=HT+1,i=1;i<=n;++i,++p,++w,++character){ 
   
        *p={ 
   *w,0,0,0,*character}; // n个字符character和它们的权重w
    }
    for(;i<=m;++i,++p)
        *p={ 
   0,0,0,0,'\0'}; // 初始化剩余结点
    for(i=n+1;i<=m;++i){ 
    // 建Huffman树
        //在HT[1..i-1]选择parent为0且weight最小的两个结点，其序号分别为s1和s2，合并后放入HT[i]
        int s1,s2;
        Select(HT,i-1,s1,s2);
        HT[s1].parent=i;HT[s2].parent=i;
        HT[i].lchild=s1;HT[i].rchild=s2;
        HT[i].weight=HT[s1].weight+HT[s2].weight;
    }
    // 从叶子到根逆向求每个字符的赫夫曼编码
    HC=(HuffmanCode)malloc((n+1)*sizeof(char *)); // 分配n个字符编码的头指针向量
    char *cd=(char *)malloc(n*sizeof(char)); // 分配求编码的工作空间
    cd[n-1]='\0';
    for(i=1;i<=n;i++){ 
    // 逐个字符求赫夫曼编码
        int start=n-1; // 编码结束符位置
        int c,f;
        for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent){ 
    // 从叶子到根逆向求编码
            if(HT[f].lchild==c) cd[--start]='0';
            else cd[--start]='1';
        }
        HC[i]=(char *)malloc((n-start)*sizeof(char)); // 为第i个字符编码分配空间
        strcpy(HC[i],&cd[start]); // 从cd复制编码（串）到HC
    }
    free(cd);
}

int main(){ 
   
    cout<<"课件上的例子……"<<endl;
    char *character = "ETAOINSRHLDCU";
    int freq[] = { 
   125,93,80,76,72,71,65,61,55,41,40,31,27};
    int n = 13;
    cout<<"13个字符及它们的频率分别是："<<endl;
    for(int i=0;i<13;i++)
        cout<<character[i]<<": "<<freq[i]<<endl;
    HuffmanTree HT;
    HuffmanCode HC;
    HuffmanCoding(HT,HC,freq,character,n);
    cout<<endl<<"Huffman编码："<<endl;
    for(int i=1;i<=n;i++){ 
   
        cout<<HT[i].character<<": "<<HC[i]<<endl;
    }
    return 0;
}