柯西中值定理:
如果函数 及
及 满足:
满足:
- 在闭区间
 上连续;
上连续; - 在开区间
 内可导;
内可导; - 对任一变量
 。
。
那么在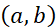 内至少有一点ξ,使等式
内至少有一点ξ,使等式
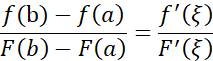
成立。
柯西中值定理证明:
1. 首先对要证的结果进行分析
根据柯西中值定理的结果,可得
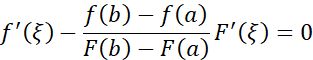
若设函数

则要证公式

成立。
由此联想到使用罗尔定理来证明,所以我们需要检查 是否等于
是否等于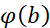 。
。
2. 证明过程
构造辅助函数

因为


可得

所以
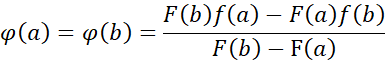
所以,根据罗尔定理,存在ξ∈(a,b),使得

整理可得
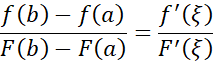
零点定理:
f(x)在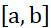 上连续,f(a)与f(b)异号,则有
上连续,f(a)与f(b)异号,则有 。
。
介值定理:
f(x)在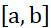 上连续,fa=A, f(b)=B, A<C<B,则有fξ=C。
上连续,fa=A, f(b)=B, A<C<B,则有fξ=C。
费马引理:
设函数f(x)在点 的一个邻域
的一个邻域 内有定义,并在点
内有定义,并在点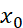 处可导,如果在邻域
处可导,如果在邻域 内
内 ,则
,则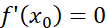 。
。
罗尔定理:
若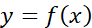 满足条件:
满足条件:
- 在闭区间
 上连续;
上连续; - 在开区间
 内可导;
内可导; - f(a)=f(b)。
则至少存在一点 ,使得
,使得 。
。

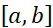 上连续;
上连续; 。
。 上连续;
上连续;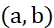 内可导;
内可导;
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/103195.html