1. 设定条件
设 f(x)∈C[a,b]f(x)∈C[a,b],且 F′(x)=f(x)F′(x)=f(x),则有:
∫abf(x) dx=F(b)−F(a)∫abf(x)dx=F(b)−F(a)
2. 定义新函数
令 Φ(x)=∫axf(t) dtΦ(x)=∫axf(t)dt,则根据微积分基本定理,有:
Φ′(x)=f(x)Φ′(x)=f(x)
3. 原函数的关系
因为 F(x)F(x) 和 Φ(x)Φ(x) 为 f(x)f(x) 的两个原函数,所以 F(x)−Φ(x)≡CF(x)−Φ(x)≡C,即存在常数 CC,使得:
F(x)−Φ(x)=CF(x)−Φ(x)=C
4. 特殊点的代入
令 x=ax=a,则有:
F(a)−Φ(a)=CF(a)−Φ(a)=C
5. 另一点的代入
令 x=bx=b,则有:
F(b)−Φ(b)=CF(b)−Φ(b)=C
6. 相减
将上述两个等式相减,得到:
F(b)−F(a)=Φ(b)−Φ(a)F(b)−F(a)=Φ(b)−Φ(a)
7. 利用 Φ(a)Φ(a) 的性质
由于 Φ(a)=∫aaf(t) dt=0Φ(a)=∫aaf(t)dt=0,因此:
Φ(b)=F(b)−F(a)Φ(b)=F(b)−F(a)
8. 得出结论
因此,我们得出结论:
∫abf(x) dx=F(b)−F(a)∫abf(x)dx=F(b)−F(a)
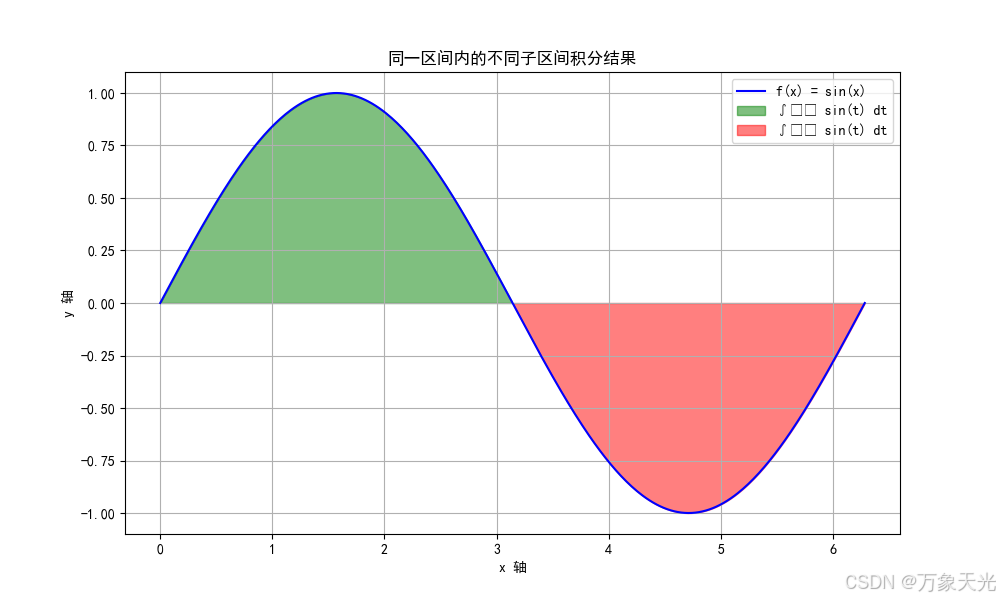
牛顿莱布尼茨公式的核心点在于它那两个设定的原函数,他们的取值范围并不相同,因为定积分是描述不规则的函数,所以两个原函数之间必定会有区别,但是将它们相减所得到的结果却是一致的,但是因为其中一个原函数,它区间内的a值是零所以得到了积分的结果是两个原函数相减的结果 ,牛顿莱布尼茨公式解决了一个最大的问题就是积分无法求解,通过这个公式我们就可以知道要想求一个积分就需要求他两个原函数之间的差便可以得到积分的结果,当然这是在一定区间内.

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/108205.html