目录

四维超立方体(Tesseract)在三维世界里的投影
事实上,现代物理学的研究工作基于的假设是,宇宙中存在至少10维的空间(弦理论的基础)。但就好像二维的纸片人无法理解3维物体一样,我们身处三维世界,更高维度的物体已经超出了常人的认知。
可以看到,四维空间里的物体转动起来,在我们眼里成了不断变化的形体。这意味着,它还有一根隐藏的轴线,当它绕着那根隐藏轴线转动时,物体凭空改变形状的事情就发生了,这样一来你还想象得出它完全体的样子吗?既然不能用感性的方法来理解,那我们不妨从数学的角度来理性的看看。
数学维度
一维物体在数学上可以看成是直线轴上的点,而一维的世界就是直线上的世界。在某个确定的“世界”中,你只需要一个数就可以确定一个点的位置,我们把它叫做x。
由于整个世界就是一条直线,所以面积这个概念是不存在的。假如你生活在一维的世界里,你看到的就只有远近不同的点或者是它们连成的线段,感觉好像非常单调,但是毕竟除了点和线段之外你也没见过别的东西,所以大概也还好。

一维世界
二维物体在数学上可以看成是平面上的形状,这个世界就是一个无边无际的平板,由两条相互垂直的轴构成,其中物体可以是各种奇怪的平面图形,当然也可以是一个点。这时,在某个确定的“世界”中,你需要两个数来确定一个点在哪,我们把它叫做(x,y)。
二维世界里想要找到别人就不太容易了,除了距离之外你还需要一个方向,当然,这里说的方向只包括前后左右这些平面里的方向。一件有趣的事情是:在二维世界中,你并不能一眼看出别人占的面积究竟有多大。因为你的视野限制在平面中,你能看到的“别人”全是一些没有厚度的线段。

二维世界
三维物体在数学上可以看成是空间上的形体,这个空间由三条相互垂直的轴构成。我们终于来到了熟悉的世界,里面的物体有长有宽也有高度/厚度。当然,在某个确定的“世界”中,你就需要三个数来确定一个点在哪,我们把它叫做(x,y,z)。
三维世界似乎已经很多姿多彩了,你能想象到的各种物件应有尽有,它们可以盘根错节,也可以规规整整,可以像云一样稀薄,也可以像铁一样坚固,还有所有一切你熟知的物理定律,化学规律。但是这一切的满足感终是源自于自己的无知,我们感叹现实世界的繁杂是因为没有体验过更高维度的世界。
三维世界
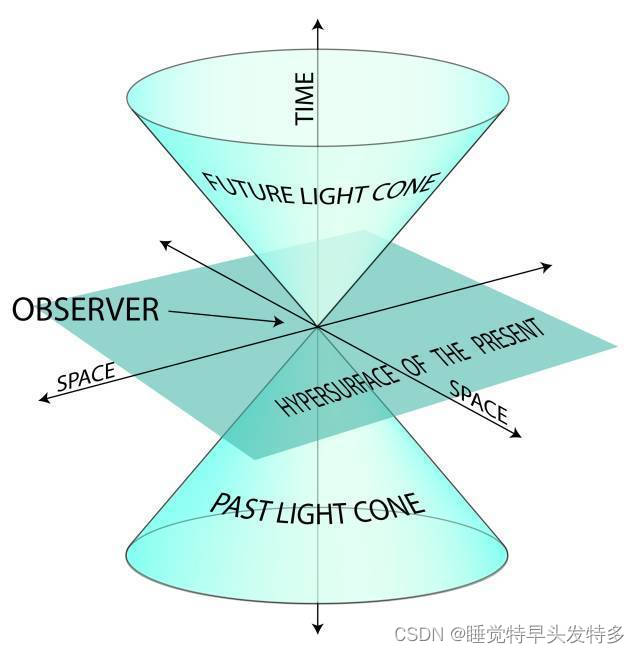
四维物体存在于四维空间中,但是我们无法在三维空间再找出一根满足垂直要求的轴线了,这第四根轴线注定不存在于我们的世界中,但是它却留下了许多传说。爱因斯坦曾把第四维度描述为时间,由此引申出了“时空”的概念,这样看来我们也是生活在四维世界中的,只是存在的位置还不够高,无法看清世界的全貌。
既然添加轴线的几何方法很难想像,我们就来尝试代数方法。从x到(x, y)再到(x, y, z),遵循规律我们得出四维空间中的点由(x, y, z, w)来描述。
但是这里多出来的w到底是干嘛的呢?我们可以理解成,这里一共存在许多个不同的三维世界,每一个世界都有一个编号,而这个编号就是w,要知道一个点在哪,我们除了知道三维空间里的位置之外,还要搞清楚它究竟在哪个三维世界里,也就是要知道w到底是几。这样一来我们就知道如何找到一个四维空间中的点了,也就可以对四维物体进行“计算”了。
以此类推,在五维空间中的点需要5个坐标才能确定(x, y, z, w, v)。
从三维世界看一切
由于我们还去不到四维世界,但是好奇宝宝那么多,想要看看四维的物体到底长什么样子的话,就需要投影到我们熟悉的三维世界来看。听起来好像很复杂,其实我们只要抓住一件事就可以了,那就是数学原理。
为了方便,我们来看看各个维度下,数学中的“球”:

二维和三维球体大家应该十分熟悉,就是圆形和球
接下来我们就开始投影吧,所谓的投影其实是一种降维。例如:
1. 要得到0维球体(原点),我们可以找一个一维球体(一段线段),只看它x=0的部分(相当于用点切割线段得到的部分);
2. 同样,要得到一维球体,我们可以找一个二维球体(一个圆),只看它y=0的部分(相当于用直线切割圆形得到的部分);
3. 接下来,二维球体可以找一个三维球体(一个球),只看它z=0的部分(相当于用平面切割球得到的部分);
4. 最后要得到三维球体,我们找一个四维球体(一个超球,hypersphere),只看它w=0的部分(相当于用三维空间切割超球得到的部分)。
类似地,如果你不想只看一种样子的投影,可以选择在别的地方切割它们,比如在不同的位置切割球,你看到的是大小不一的圆。也就是说,如果你面前有一个四维空间里的超球,当w改变数值大小的时候,你能看到的就是这个球在变大或者缩小。这样一来,我们就完成了四维物体的投影!

当四维超球穿过三维空间时我们看到的景象

当球体穿过二维平面时的景象
正是用这种投影的办法,我们得以窥见四维空间里小小的一部分,继续类比下去,更高维度的物体也可以被投影到大家熟悉的三维空间中来。
基于数学的方法,我们的确找到了很多高维度物体的特性,甚至利用维度的变换成功证明了一些猜想(封闭曲线的内接矩形问题)。但是到目前为止,我们还是没有办法完全了解和想象出高维度世界的全貌。
什么是维度?

三维空间
一维数轴,二维平面,三维立体,人类是三维动物,活在四维空间里。
三维空间有长度、宽度与高度。

四维空间
四维比三维多一维,它就是时间!

五维空间

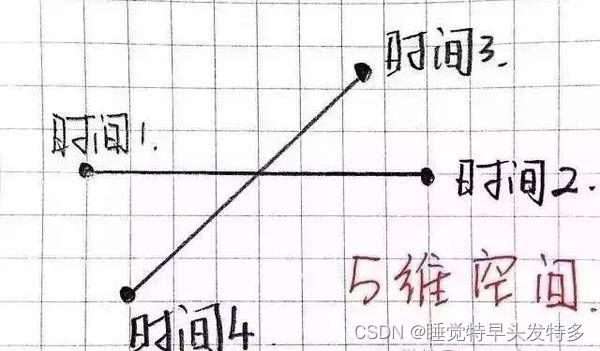
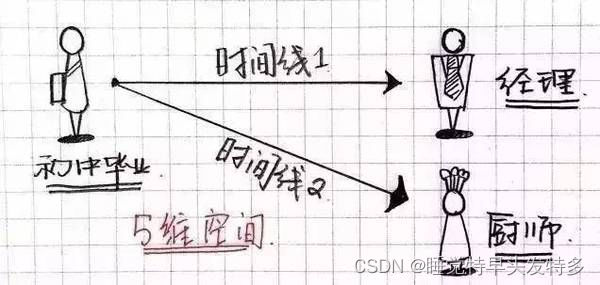

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/96929.html