文章目录
《结构方程模型 AMOS 的操作与应用》——读后总结
一、基本概念
1、测量模型
测量模型由 潜在变量 (latent variable) 与 观察变量 (observed variable; 又称测量变量) 组成。就数学定义而言,测量模型是一组观察变量的线性函数,观察变量优势又称为潜在变量的外显变量 (manifest variables 也称显性变量) 或测量指标 (measured indicators) 或指标变量。
在 SEM 模型中,观察变量通常以长方形或方形符号表示,而潜在变量 (latent variables) 或称构念 (construst) 通常以椭圆形或圆形符号表示。

上述测量模型的回归方程式如下:
X 1 = λ 1 ξ 1 + δ 1 X 2 = λ 2 ξ 1 + δ 2 X 3 = λ 3 ξ 1 + δ 3 Y 1 = λ 1 η 1 + ϵ 1 Y 2 = λ 2 η 1 + ϵ 2 Y 3 = λ 3 η 1 + ϵ 3 X1=\lambda_1\xi_1+\delta_1\\ X2=\lambda_2\xi_1+\delta_2\\ X3=\lambda_3\xi_1+\delta_3\\ Y1=\lambda_1\eta_1+\epsilon_1\\ Y2=\lambda_2\eta_1+\epsilon_2\\ Y3=\lambda_3\eta_1+\epsilon_3 X1=λ1ξ1+δ1X2=λ2ξ1+δ2X3=λ3ξ1+δ3Y1=λ1η1+ϵ1Y2=λ2η1+ϵ2Y3=λ3η1+ϵ3
上述的回归方程式可以矩阵方程式表示如下:
X = Λ X ξ + δ Y = Λ Y η + ϵ X=\Lambda_X\xi+\delta\\ Y=\Lambda_Y\eta+\epsilon X=ΛXξ+δY=ΛYη+ϵ
其中 ϵ \epsilon ϵ 与 η 、 ξ \eta、\xi η、ξ 及 δ \delta δ 无相关,而 δ \delta δ 与 ξ 、 η \xi、\eta ξ、η 及 ϵ \epsilon ϵ 也无相关。 Λ X \Lambda_X ΛX 与 Λ Y \Lambda_Y ΛY 为指标变量( X 、 Y X、Y X、Y)的因素负荷量 (loading),而 δ 、 ϵ \delta、\epsilon δ、ϵ 为外显变量的测量误差, ξ 、 η \xi、\eta ξ、η 分别为外衍潜在变量 (exogenous latent variable) 与内衍潜在变量 (endogenous latent variables)。 SEM 测量模型中假定:潜在变量(共同因素)与测量误差间不可能有共变关系或因果关系路径存在。
以观察变量作为潜在变量的指标变量,根据指标变量性质的不同,可以区分为 反映性指标 (reflective indicators) 与 形成性指标 (formative indicators) 两种。反映性指标又称为果指标 (effect indicators),其指标变量为“果”,而潜在变量为“因”;相对的,形成性指标又称为因指标或成因指标,其指标变量是“因”,潜在变量为“果”。
如下图所示,左边为反映性指标,右边为形成性指标。
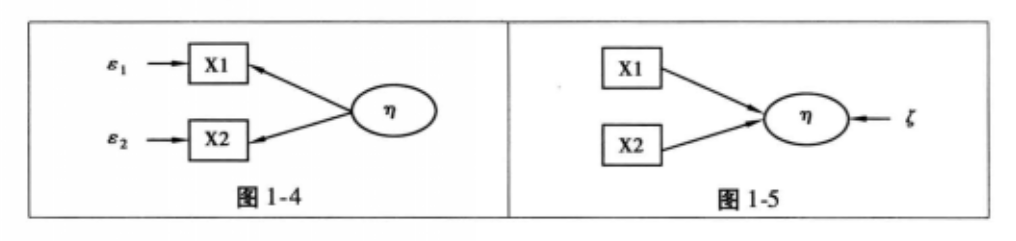
反映性指标的回归方程式如下,其中 β 1 、 β 2 \beta_1、\beta_2 β1、β2 为估计的参数, ϵ 1 、 ϵ 2 \epsilon_1、\epsilon_2 ϵ1、ϵ2 为测量的误差。
X 1 = β 1 η + ϵ 1 X 2 = β 2 η + ϵ 2 X1=\beta_1\eta+\epsilon_1\\ X2=\beta_2\eta+\epsilon_2 X1=β1η+ϵ1X2=β2η+ϵ2
形成性指标的回归方程式如下,其中 γ 1 、 γ 2 \gamma_1、\gamma_2 γ1、γ2 为估计的参数,而 δ \delta δ 为残差。
η = γ 1 X 1 + γ 2 X 2 + δ \eta=\gamma_1X1+\gamma_2X2+\delta η=γ1X1+γ2X2+δ
在 Amos 测量模型中,需要有一个测量指标的路径系数 λ \lambda λ 固定为 1 1 1,否则测量模型无法估计。

测量模型在 SEM 的模型中就是一般所谓的验证式因素分析 (confirmatory factor analysis; CFA),验证式因素分析的技术用于检验数个测量变量可以构成潜在变量的程度,验证式因素分析即在检验测量模型中的观察变量 X X X 与潜在变量 ξ \xi ξ 间的因果模型是否与观察数据契合。在 SEM 模型分析中的变量又可以区分为外因变量 (exogenous variables) 与内因变量 (endogenous variables)。外因变量指未受到任何其他变量的影响,但却直接影响其他变量的变量;内因变量值在模型中会受到任一变量影响的变量。
2、结构模型
结构模型即是潜在变量间因果关系模型的说明,作为因的潜在变量即称为外因潜在变量,作为果的潜在变量即称为内因潜在变量。在 SEM 分析模型中,只有测量模型而无结构模型的回归关系,即为验证性因素分析;相反的,只有结构模型而无测量模型,则潜在变量间因果关系的探讨,相当于传统的路径分析(或称径路分析, path analysis),其中的差别在于结构模型探讨潜在变量间的因果关系,而路径分析直接探讨观察变量间的因果关系。
结构模型的结构方程式,如下所示:
Y i = B 0 + B 1 X i 1 + B 2 X i 2 + . . . + B p X i p + ϵ i Y_i=B_0+B_1X_{i1}+B_2X_{i2}+...+B_pX_{ip}+\epsilon_i Yi=B0+B1Xi1+B2Xi2+...+BpXip+ϵi
其中, ϵ i \epsilon_i ϵi 为残差值, B B B 为结构系数矩阵。
结构模型与测量模型的简易关系如下图所示。一个广义的结构方程模型,包括数个测量模型及一个结构模型。

Amos 绘制 SEM 理论模型图有几个基本假定:
- (1) 测量模型中的测量指标的测量误差项的路径系数内定为 1 1 1(也可将其改为界定误差项的方差等于 1 1 1 );
- (2) 测量模型中必须有一个指标变量的路径系数内定为 1 1 1,以上两个固定参数在绘制测量模型时AMOS会自动增列所有观察变量、潜在变量、误差变量的名称为唯一,不能重复出现;
- (3) 作为内因潜在变量或内因观察变量(路径分析模型)者要增列一个残差项,所有外因潜在变量间要以双箭头图像钮建立共变关系;
C 1 C1 C1 表示共变关系; V 1 V1 V1 至 V 13 V13 V13 为变量的方差,SEM 分析程序中作为内因潜在变量者无法估计其方差,所以内因潜在变量 F 3 、 F 4 F3、F4 F3、F4 无法增列方差参数; W 1 W1 W1 至 W 9 W9 W9 为路径系数,在测量模型中为因素负荷量。

在上图中,模型的变量总共有 24 24 24 个,观察变量有 9 9 9 个 ( SEM 模型中有九个测量指标变量 ),无法观察的变量有 15 15 15 个,包括四个潜在变量 F l 、 F 2 、 F 3 、 F 4 Fl、F2、F3、F4 Fl、F2、F3、F4 ( ξ 1 、 ξ 2 、 η 1 、 η 2 ) \xi_1、\xi_2、\eta_1、\eta_2) ξ1、ξ2、η1、η2),九个测量误差项,两个内因观察变量的残差项 ( err1, err2 ),外因变量有 13 13 13 个 ( 九个测量误差项、两个残差项、两个潜在变量 F 1 F1 F1 和 F 2 F2 F2 )、内因变量有 11 11 11 个 ( 九个观察变量和 F 3 、 F 4 F3、F4 F3、F4 两个潜在变量 ) 。
3、结构方程模型图中的符号与意义


4、参数估计
在 SEM 分析中,提供七种模型估计的方法:工具性变量法( instrumental variables;IV法 )、两阶段最小平方法( two-stage least squares;TSLS法 )、未加权最小平方法(unweightedleast squares;ULS法 )、一般化最小平方法( generalized least squares;GLS法 )、一般加权最小平方法( generally weighted least squares;GWLS法或WLS法 )、极大似然法( MaximumLikelihood;ML法 )、对角线加权平方法( diagonally weighted least squares;DWLS法 )。研究者如要检验样本数据所得的协方差矩阵( S S S 矩阵)与理论模型推导出的协方差矩阵( ∑ ^ \hat{\sum} ∑^ 矩阵)间的契合程度,即是模型适配度的检验,测量 矩阵如何近似S矩阵的函数称为适配函数(fitting function),不同的适配函数有不同的估计方法。
只有是大样本并且假设观察数据符合多变量正态性,卡方检验才可以合理使用,此时,使用 ML 估计法最为合适;如果数据为大样本,但观察数据不符合多变量正态性假定,最好采用GLS估计法(周子敬,2006)。
二、模型适配度统计量
1、模型适配度检验指标
适配度指标 (goodness-of-fit indics) 是评价假设的路径分析模型图与搜集的数据是否相互适配,而不是说明路径分析模型图的好坏,一个适配度完全符合评价标准的模型图不一定保证是个有用的模型,只能说研究者假设的模型图比较符合实际数据的现况。
在进行 SEM 模型分析时,需对模型进行违反估计检验。模型违反估计有以下几种常见情形:
- 出现负的方差。一般来说,误差方差愈小愈好,其最小值为 0 0 0 ,表示没有测量误差,若是为负数,则违反了估计;
- 协方差间标准化估计值的相关系数大于 1 1 1;
- 协方差矩阵或相关矩阵不是正定矩阵;
- 标准化系数超过或非常接近 1 1 1;
- 出现非常大的标准误差 (very large standard errors),或标准误差为极端小的数值,如接近 0 0 0;
2、整体模型适配度指标
(1)绝对适配度指标
① 卡方值 X 2 X^2 X2
卡方值 ( X 2 X^2 X2) 越小表示实际矩阵和输入矩阵的差异越小,一个不显著 ( p > 0.05 p>0.05 p>0.05 ) 的卡方值表示假设模型与实际数据的拟合程度越好;反之,若是 X 2 X^2 X2 值显著,则说明实际矩阵和输入矩阵间不适配,拟合程度差。饱和模型 ( Saturatedmodel ) 是假定模型完全适配样本数据的模型,因而其 X 2 X^2 X2 值为 0 0 0。卡方值受样本量的大小非常敏感,样本数越大,则卡方值越容易达到显著,导致理论模型遭到拒绝的概率越大,模型拟合程度差的概率越大。
在 Amos 的文字输出中,表格会呈现五个估计量数:【NPAR】栏为模型中待估计的独特参数数目 ( 自由参数数目 );【CMIN】栏为模型的卡方值,数值即为最小样本差异函数值 C ^ \hat{C} C^;【DF】栏为检验模型自由度的数目,自由度等于样本矩提供的数据点数目与模型内待估计自由参数数目的差值;【P】栏是卡方值检验的显著性概率值;【CMIN/DF】为卡方与自由度的比值。

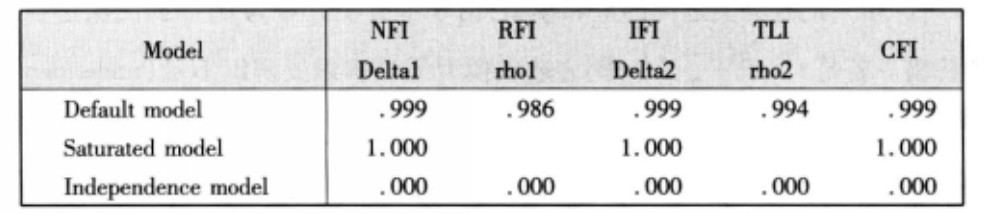
报表中有三个模型,此三个模型为预设模型 ( default model,预设模型即为理论模型 ) 、饱和模型 ( saturated model )、独立模型 ( independent model ),要检核理论模型与实际数据是否适配或契合,应查看预设模型的 CMIN值。
② 卡方自由度比 ( NC )
卡方自由度比值 ( X 2 ÷ d f X^2\div df X2÷df ) 愈小,表示假设模型的协方差矩阵与观察数据愈适配;相对的,卡方自由度比值愈大,表示模型的适配度愈差。一般而言,卡方自由度比值小于2时,表示假设模型的适配度较佳 (Carmines&McIver,1981) 。卡方自由度比也称为规范卡方 ( Normed chi-square;NC ):①当其值小于 1.00 时,表示模型过度适配,即该模型具有样本独异性;②当其值大于 2.0 或 3.0 ( 较宽松的规定值是 5.0 ),则表示假设模型尚无法反映真实观察数据,即模型契合度不佳,模型需要改进。
③ RMR & SRMR & RMSEA
RMR 为残差均方和平方根 ( root mean square residual ),RMR 值等于适配残差 ( fitted residual ) 方差协方差的平均值的平方根。RMR 值要越小越好,越小的 RMR 值表示模型的适配度越佳,一般而言,其值在 0.05 0.05 0.05 以下是可接受的适配模型。
SRMR 为标准化残差均方和平方根 ( standardized root mean square residual ),其值为平均残差协方差标准化的总和,值介于 0 − 1 0-1 0−1 之间。 SRMR 值要越小越好,越小的 SRMR 值表示模型的契合度越佳,一般而言,其值在 0.05 0.05 0.05 以下是可接受的适配模型。
RMSEA ( root mean square error of approximation ),RMSEA 值通常被视为最重要的适配指标信息。RMSEA 为一种不需要基准线模型的绝对性指标,其值越小,表示模型的适配度越佳,一般而言,当 RMSEA 的数值高于 0.10 0.10 0.10 以上时,则模型的适配度欠佳;其值在 0.08 − 0.10 0.08-0.10 0.08−0.10 之间则是模型尚可,具有普通适配度 ( mediocre fit );在 0.05 − 0.08 0.05-0.08 0.05−0.08 之间表示模型良好,即有合理适配 ( reasonable fit );而如果其数值小于 0.05 0.05 0.05 表示模型适配度非常好 ( good fit )。在 Amos 中,会提供 RMSEA 值虚无假设 ( H 0 : R M S E A ≤ 0.05 H_0:RMSEA≤0.05 H0:RMSEA≤0.05 ) 检验的显著 P P P 值;当 RMSEA 值小于 0.05 0.05 0.05 ,表示模型适配度佳。
④ GFI & AGFI
GFI 为适配度指标,也称为良适性适配指标 ( goodness-of-fit index )。GFI 数值介于 0 − 1 0-1 0−1 间,其数值愈接近 1 1 1,表示模型的适配度愈佳;GFI 值愈小,表示模型的契合度愈差。一般的判别标准为 GFI 值大于 0.90 0.90 0.90,表示模型路径图与实际数据有良好的适配度。
AGFI 为调整后适配度指数,或称为调整后良适性适配指标 ( adjusted goodness-of-fit index )。调整后的 GFI 值不会受到单位的影响。一般的判别标准为 AGFI 值大于 0.90 0.90 0.90,表示模型路径图与实际数据有良好的适配度。
(2)增值适配指标
在 Amos 输出的模型适配指标中,有一项基准线比较 ( baseline comparisons ) 指标参数,包含五种指标:NFI、RFI、IFI、TLI、CFI。其中,NFI 为规范拟合指标 ( normed fit index );RFI 为相对拟合指标 ( relative fit index );IFI 为增值拟合指标 ( incremental fit index );TLI 为非规准拟合指标 ( Tacker-Lewis index = non-normed fit index, NNFI );CFI 为比较拟合指标 ( comparative fit index )。其值大多介于 0 − 1 0-1 0−1 之间,且越接近 1 1 1 表示模型适配度越高;越接近 0 0 0 表示模型契合度越低。一般认为,其标准值均为 0.90 0.90 0.90 以上。
(3)简约适配指标
① AIC &CAIC
AIC 值的概念与 PNFI 值的概念类似,在进行模型适配度检验时,期望其数值愈小愈好,越接近 0 0 0,表示模型的契合度愈高且模型愈简约。AIC 值的数值愈小表示模型的适配度愈佳,它的主要功能是用于数个模型之间的比较。
CAIC 指标是 AIC 指标的调整值。在判断假设模型是否可以接受时,通常的原则是理论模型的 AIC 值必须比饱和模型以及独立模型的 AIC 值小;假设模型的 CAIC 值必须比饱和模型以及独立模型的 CAIC 值小。若在多个模型中进行选择时,则应当选取 AIC / CAIC 值中最小者。其中有一点需要注意,使用 AIC 指标与 CAIC 指标时,样本的大小至少要在 200 200 200 以上,且数据要符合多变量正态分布,否则指标探究的结果缺乏可靠性。

② PNFI
PNFI 为简约调整后的规准适配指数 ( parsimony-adjusted NFI )。PNFI 主要使用于不同自由度的模型之间的比较,其值愈高愈好。一般而言,当比较不同的模型时,PNFI 值的差异在 0.06 − 0.09 0.06-0.09 0.06−0.09 间,被视为是模型间具有真实的差异存在(黄芳铭,2005)。如不做模型比较,只关注于假设模型契合度判别时,一般以 P N F I > 0.50 PNFI>0.50 PNFI>0.50 作为模型适配度通过与否的标准,亦即 PNFI 值在 0.50 0.50 0.50 以上,表示假设理论模型是可以接受的。
③ PGFI
PGFI 为简约适配度指数 ( parsimony goodness-of-fit index ),其性质与 PNFI 指标值相同,PGFI 的值介于。与 1 1 1 之间,其值愈大,表示模型的适配度愈佳 ( 模型愈简约 )。判别模型适配的标准,一般皆采 P G F I > 0.50 PGFI>0.50 PGFI>0.50 为模型可接受的范围。
3、模型内在结构适配度的评估
内在结构适配的评价包括以下两个方面:一为测量模型的评价;二为结构模型的评价。前者关注于测量变量是否足以反映其相对应的潜在变量,其目标在于了解潜在建构的效度与信度;后者是评价理论建构阶段所界定的因果关系是否成立。其中,信度指的是测量的一致性,即关注测量结果在不同时间、不同条件或不同测量者下是否保持稳定和一致;而效度,所反映的则是指标变量 ( 外显变量 ) 对于其想要测量的潜在特质,实际测量的程度。
(1)效度分析
在 SEM 中,效度分析即是潜在变量与其指标变量间路径 ( 因素负荷量 ) 的显著性检验。如果测量模型中的因素负荷量均达显著 ( p < 0.05 p<0.05 p<0.05, t t t 的绝对值大于 1.96 1.96 1.96 ),此种情形表示测量的指标变量能有效反映出它所要测量的构念 ( 潜在变量 ),该测量具有良好的效度证据 ( validity evidence )。其中,测量误差也要达显著 ( p < 0.05 p<0.05 p<0.05, t t t 的绝对值大于 1.96 1.96 1.96 ),但测量误差不能为 0 0 0。
在 Amos 中,以临界比值 ( critical ratio; C.R. ) 代表 t t t 值。临界比是参数估计值除以其标准误,其功能在统计检验上很像 Z Z Z 统计量,可以检验参数估计值是否显著不等于 0 0 0,在显著水平 a a a 为 0.05 0.05 0.05 时,C.R. 的绝对值如果大于 1.96 1.96 1.96,可以拒绝虚无假设 ( 参数估计值等于 0 0 0 ),接受对立假设 ( 表示参数估计值显著不等于 0 0 0 )。对于没有达到 0.05 0.05 0.05 显著水平的不应直接删除,应从增加实征数据的样本观察值着手。
(2)信度分析
信度分析可以使用 R 2 R^2 R2 值来衡量。当 R 2 R^2 R2 达到显著,则其值越高,表示指标变量 ( 外显变量 ) 具有良好的信度;反之,信度不佳。
① 潜变量的组合信度 CR ( composite reliability ) 在 0.6 0.6 0.6 以上;
组合信度 = C R = ( ∑ λ ) 2 [ ( ∑ λ ) 2 + ∑ θ ] = ( ∑ 因素负荷量 ) 2 [ ( ∑ 因素负荷量 ) 2 + ∑ 测量误差变异量 ] 组合信度=CR=\frac{(\sum \lambda)^2}{[(\sum \lambda)^2+\sum \theta]}=\frac{(\sum因素负荷量)^2}{[(\sum因素负荷量)^2+\sum测量误差变异量]} 组合信度=CR=[(∑λ)2+∑θ](∑λ)2=[(∑因素负荷量)2+∑测量误差变异量](∑因素负荷量)2
② 指标变量个别项目的信度 ( 标准化系数值的平方 ) 应大于 0.50 0.50 0.50,因素负荷量应介于 0.50 − 0.95 0.50-0.95 0.50−0.95 之间;
③ 潜在变量的平均方差抽取量 AVE ( average variance extracted ) 表示相较于测量误差变异量的大小,潜在变量构念所能解释指标变量变异量的程度。潜在变量平均方差抽取值的大小若是在 0.50 0.50 0.50 以上,表示指标变量可以有效反映其潜在变量,该潜在变量便具有良好的信度与效度;
④ 所有参数统计量的估计值均达到显著水平 ( t t t 值绝对值 > 1.96 >1.96 >1.96,或 p < 0.05 p<0.05 p<0.05 );
⑤ 标准化残差 ( standardizede residuals ) 的绝对值必须小于 2.58 2.58 2.58 ( 或 3 3 3 );
⑥ 修正指标 ( modification indices ) 小于 3.84 3.84 3.84,在 Amos 操作中内定的修正指标值界限为 4.00 4.00 4.00;
4、自由度 & 自由参数的计算
假设 SEM 模型中共有 p 个外因测量指标 ( 外衍观察变量 )、q 个内因测量指标 ( 内衍观察变量 ),则形成的数据点数目 = 1 2 ( p + q ) ( p + q + 1 ) =\frac{1}{2}(p+q)(p+q+1) =21(p+q)(p+q+1) 个,数据点数目包含所有观察变量的协方差与方差。若待估计的自由参数个数有 t t t 个,则模型的自由度 d f = 1 2 ( p + q ) ( p + q + 1 ) − t df=\frac{1}{2}(p+q)(p+q+1)-t df=21(p+q)(p+q+1)−t。
以下图为例,在路径分析模型图中有三个外因观察变量、两个内因观察变量,则
样本数据点数目 = 1 2 ( p + q ) ( p + q + 1 ) = 1 2 ( 3 + 2 ) ( 3 + 2 + 1 ) = 15 样本数据点数目=\frac{1}{2}(p+q)(p+q+1)=\frac{1}{2}(3+2)(3+2+1)=15 样本数据点数目=21(p+q)(p+q+1)=21(3+2)(3+2+1)=15
故而 15 15 15 个样本协方差矩阵如下所示:


以上图的模型为例,自由参数 ( 待估计参数 ) 包括 3 3 3 个协方差 ( C1、C2、C3 )、 5 5 5 个方差 ( V1、V2、V3、V4、V5 )、 7 7 7 个回归系数 ( W1、W2、W3、W4、W5、W6、W7 ),自由参数的数目 = 3 + 5 + 7 = 15 = t =3+5+7=15=t =3+5+7=15=t。
5、三种模型识别
① 正好识别模型:即模型的自由度 d f df df 等于自由参数 t t t 的数值( d f = t df=t df=t );
② 过度识别模型:即模型的自由度 d f df df 大于自由参数 t t t 的数值( d f > t df>t df>t );
③ 低度识别模型:即模型的自由度 d f df df 小于自由参数 t t t 的数值( d f < t df<t df<t );
其中,Amos 分析需要过度识别模型,否则将会无法求解 ( 正好识别模型可以求得参数的唯一解;低度识别模型无法求得参数的唯一解 )。
在测量模型的识别方面,必须考虑到潜在变量的量尺度的界定问题。由于潜在变量并非观察变量,没有特定的矩阵尺度,因而必须给潜在变量一个特定的单位尺度,其界定的方式有两种:一为将潜在变量的方差设定为 1 1 1,将潜在变量限制为以标准化方差来作为共同单位;二为在潜在变量的测量指标中限定一个观察变量的路径系数为一个不等于 0 0 0 的数值(一般界定等于 1 1 1),将测量变量的单位设定为潜在变量的参考量尺,使得潜在变量的方差得以自由估计,表示观察变量因素负荷量参数均在测量相同的因素构念。
三、Amos 软件
1、结果分析
在 Amos 中运行分析后,【View Text】后有个【Amos Output】窗口,里面可能有以下选项:


① Notes for Model
在该选项中,窗口里会输出自由度值、适配卡方值、显著性概率值等指标。对于显著性概率值,若是其未达到 0.05 0.05 0.05 的显著水平,则接受了虚无假设,表示观察数据的 S S S 矩阵与假设模型隐含的 ∑ ^ \hat{\sum} ∑^ 矩阵相契合,即模型拟合效果不错。
② Estimates
在该选项中,可以看到有非标准化的回归系数及其显著性检验摘要表,右边第一列估计值为非标准化的回归系数,第二列为估计参数的标准误(standard error),第三列 C.R. 为检验统计量(临界比,critical ratio),临界比值为 t t t 检验的 t t t 值,此值如果大于 1.96 1.96 1.96 表示达到 0.05 0.05 0.05 显著水平,第四栏 p 值为显著性,如果 p < 0.001 p<0.001 p<0.001,会以符号“*”表示,若是 p > 0.001 p>0.001 p>0.001,会直接呈现 p 值的大小。

下表为标准化的回归系数值(Beta值),亦即路径分析中的路径系数。

外因观察变量间的协方差及协方差显著性检验,三个外因变量(预测变量)间的协方差均达到 0.05 0.05 0.05 显著水平:

三个外因观察变量间的相关系数,当协方差达到显著水平,则其相对应的积差相关系数也会达到 0.05 0.05 0.05 显著水平:

下面两个表分别为假设模型所导出的协方差矩阵(隐含协方差矩阵)与相关矩阵(隐含相关系数矩阵):

2、饱和模型 & 独立模型
① 饱和模型
所谓饱和模型是指假设模型中所有待估计的参数正好等于协方差矩阵中的素,假设建构模型中有 p 个外因观察变量,q 个内因观察变量,则所形成的协方差中独特素的总数 = 1 2 ( p + q ) ( p + q + 1 ) =\frac{1}{2}(p+q)(p+q+1) =21(p+q)(p+q+1) 个,若是模型界定中所估计的参数个数 k 刚好等于 1 2 ( p + q ) ( p + q + 1 ) \frac{1}{2}(p+q)(p+q+1) 21(p+q)(p+q+1) 个,则形成唯一解,此种情形会造成模型的自由度为 0 0 0,卡方值也等于 0 0 0,成为刚好识别 ( just identified model ) 的模型,模型与数据间形成完美的适配 ( perfect fit )。
② 独立模型
在独立模型中所有变量两两间均是相互独立而没有关系的,即两两变量间既没有以双箭号建立共变关系,也没有以单箭号建立因果关系。
3、模型修正
修正指标时需注意的几点:
- 放宽最大修正指标的参数,并不一定能保证让模型得到一个实质的解释意义;
- 若同时有数个修正指标值很大,研究者应一次放宽一个参数 ( one at a time ),将其从固定参数改为自由参数,重新估计模型,而不要一次放宽数个参数.再对模型加以估计;
- 修正指标必须配合期望参数改变量 ( expected parameter change; EPC 值 ),所谓期望参数改变量即当固定参数被放宽修正而重新估计时,所期望获得的该参数估计值的改变量.如果修正指标值 ( MI 值 ) 较大,且相对应的期望参数改变量也较大,表示修正该参数会带来期望参数改变量的数值也较大,且此种修正,可以明显降低卡方值,此种修正才有显著的实质意义 ( Diamantopoulos & Siguaw, 2000; 余民宁, 2006 );
回归系数的修正指标会增列新的路径系数供研究者参考,其中有些路径系数不符合 SEM 的假定,研究者在增列路径系数时要小心,不符合 SEM 假定的路径包括:测量指标的误差项对潜在变量的影响路径、测量指标变量对其他测量指标变量的影响路径、测量指标的误差项对其他测量指标的影响路径、测量指标的误差项对其他测量指标的误差项的影响路径等。
四、验证性因素分析 ( CFA )
探索性因素分析的目的在于确认量表因素结构 ( factor structure ) 或一组变量的模型.常考虑的是要决定多少个因素或构念,同时因素负荷量的组型如何。验证性因素分析通常会依据一个严谨的理论.或在实征基础上,允许研究者事先确认一个正确的因素模型,这个模型通常明确将变量归类于那个因素层面中,并同时决定因素构念间是相关的.与探索性因素分析相比,验证性因素分析有较多的理论检验程序。验证性因素分析模型被归类于一般结构方程模型或共变结构模型 ( covariance structure model ) 之中,允许反映与解释潜在变量,它和一系列的线性方程相连结。
两种模型的基本目标是相似的,皆在解释观察变量间的相关或共变关系,但 CFA 偏重于检验假定的观察变量与假定的潜在变量间的关系 ( Everitt & Dunn, 2001 )。
一个有六个外显变量、两个因素构面的 CFA 路径图如下图所示:两个共同因素各有三个测量指标变量,每个指标变量均只受到一个潜在变量的影响,因而是一种单向度测量模型。在单向度测量模型中,如果观察变量 X 1 、 X 2 、 X 3 X1、X2、X3 X1、X2、X3 测量的潜在特质构念同质性很高,则观察变量 X 1 、 X 2 、 X 3 X1、X2、X3 X1、X2、X3 间的相关会呈现中高度关系,三个测量指标的因素负荷量会很大;若是观察变量 X 4 、 X 5 、 X 6 X4、X5、X6 X4、X5、X6 测量的潜在特质构念同质性很高,则观察变量 X 4 、 X 5 、 X 6 X4、X5、X6 X4、X5、X6 间的相关会呈现中高度关系,三个测量指标的因紊负荷量会很大 ( 一般要求标淮是 λ > 0.71 \lambda>0.71 λ>0.71 )。此结果表示测量同一特质构念的测量指标会落在同一个因素构念上,此种效度称为聚合效度 ( convergent validity ) 。在测量模型中,若是任何两个因素构念间的相关显著不等于 1 1 1,表示两个因素构念间是有区别的.此种效度称为区别效度 ( discriminant validity ),具有区别效度的测量模型,测量不同因素构念的测量指标变量会落在不同因素构念上,而测量相同因素构念的观察变量会落在同一个因素构念之上。

在 CFA 测量模型中,每个潜在变量的指标变量中要有一个测量指标路径系数 λ \lambda λ 固定为 1 1 1 。

1、一阶验证性因素分析——多因素斜交模型
输出结果:
① 样本矩阵

矩阵中的每个素(除了对角线上的素)表示两个变量之间的协方差,而对角线上的素则表示各变量的方差。协方差值的正负表示两个变量之间的变化趋势是否一致(正相关或负相关),其绝对值大小则反映了这种趋势的强度。较大的协方差值表明两个变量之间的线性关系较强,而较小的协方差值(尤其是接近 0 0 0 的值)则表明两个变量之间的线性关系较弱或不存在。

样本相关系数矩阵是观测变量之间相关系数的集合,它是对协方差矩阵进行标准化处理后的结果。相关系数矩阵中的每个素(无论是对角线上的还是非对角线上的)都表示两个变量之间的线性相关程度,其值域为 [ − 1 , 1 ] [-1, 1] [−1,1]。
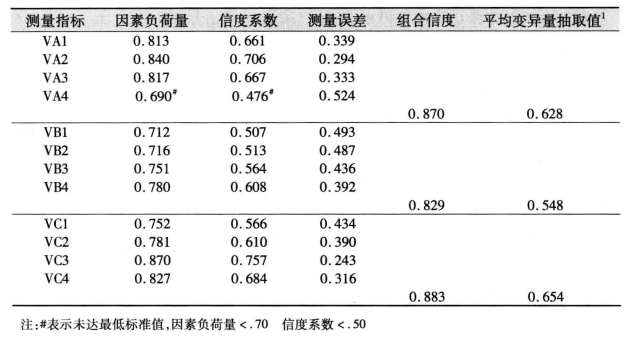
② 因素负荷量 & 组合信度 & 平均变异量抽取值

Standardized Regression Weights 为标准化回归系数,在验证性因素分析中也称为因素加权值 ( factor weights ) 或因素负荷量 ( factor loading ) ,标准化的路径系数代表的是共同因素对测量变量的影响。因素负荷量值介于 0.50 − 0.95 0.50-0.95 0.50−0.95 之间,表示模型的基本适配度良好,因素负荷量愈大,表示指标变量能被构念解释的变异愈大,指标变量能有效反映其要测得的构念特质。若是因素构念中有中高度相关 ( 因素间的相关系数 > 0.75 >0.75 >0.75 ) 存在,故考虑采用斜交 CFA 模型。
根据获得的因素负荷量和测量误差即可根据组合信度的公式求得每组的组合信度值,从而得到下表:
C R = ( ∑ λ ) 2 [ ( ∑ λ ) 2 + ∑ ( θ ) ] = ( ∑ 标准化因素负荷量 ) 2 [ ( ∑ 标准化因素负荷量 ) 2 + ∑ ( θ ) ] CR=\frac{(\sum\lambda)^2}{[(\sum\lambda)^2+\sum(\theta)]}=\frac{(\sum标准化因素负荷量)^2}{[(\sum标准化因素负荷量)^2+\sum(\theta)]} CR=[(∑λ)2+∑(θ)](∑λ)2=[(∑标准化因素负荷量)2+∑(θ)](∑标准化因素负荷量)2

其中,若是潜在变量的组合信度值在 0.60 0.60 0.60 以上,表示模型的内在质量理想;平均变异量抽取值的一般判别标准为其值大于 0.50 0.50 0.50 。
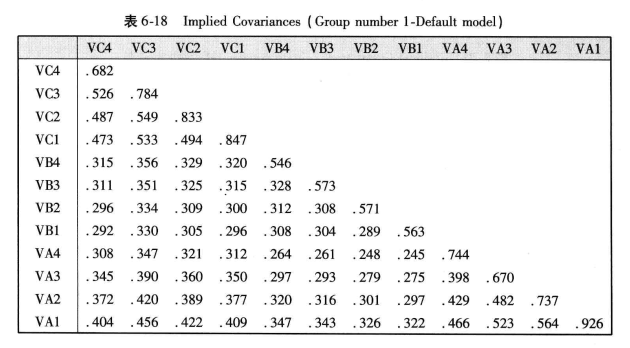
③ 隐含样本矩阵
隐含方差矩阵 ( Implied Covariances ) 为假定模型是正确的情况下,观察变量总体协方差的估计结果和观察变量间的相关估计值。

根据获得的因素负荷量和测量误差即可根据组合信度的公式求得每组的组合信度值,从而得到下表:
C R = ( ∑ λ ) 2 [ ( ∑ λ ) 2 + ∑ ( θ ) ] = ( ∑ 标准化因素负荷量 ) 2 [ ( ∑ 标准化因素负荷量 ) 2 + ∑ ( θ ) ] CR=\frac{(\sum\lambda)^2}{[(\sum\lambda)^2+\sum(\theta)]}=\frac{(\sum标准化因素负荷量)^2}{[(\sum标准化因素负荷量)^2+\sum(\theta)]} CR=[(∑λ)2+∑(θ)](∑λ)2=[(∑标准化因素负荷量)2+∑(θ)](∑标准化因素负荷量)2
其中,若是潜在变量的组合信度值在 0.60 0.60 0.60 以上,表示模型的内在质量理想;平均变异量抽取值的一般判别标准为其值大于 0.50 0.50 0.50 。
③ 隐含样本矩阵
隐含方差矩阵 ( Implied Covariances ) 为假定模型是正确的情况下,观察变量总体协方差的估计结果和观察变量间的相关估计值。
.

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/99751.html