数据特征分析方法总结怎么写_定量分析的基本步骤

数据特征分析方法总结

21世纪是大数据的时代，因为这些大数据中蕴含着时代发展的信息。如何科学地分析数据特征是数据分析师必须掌握的基础技能之一。因此，我今天主要希望通过理论推导并实现一些常用的数据特征分析方法来加强对数据特征处理的能力。

分布分析

分布分析:研究数据的分布特征和分布类型，分为定量数据和定性数据，并通过这两种类型来区分基本统计量。
常用指标为：极差、频率分布情况、分组组距及组数

# 读取数据
data = pd.read_csv('data/深圳罗湖二手房信息.csv', engine='python', encoding='gbk')
plt.scatter(data['经度'], data['纬度'],
            s=data['房屋单价'] / 500,
            c=data['参考总价'], cmap='Reds',
            alpha=0.4)
plt.grid()
plt.show()
data.head()

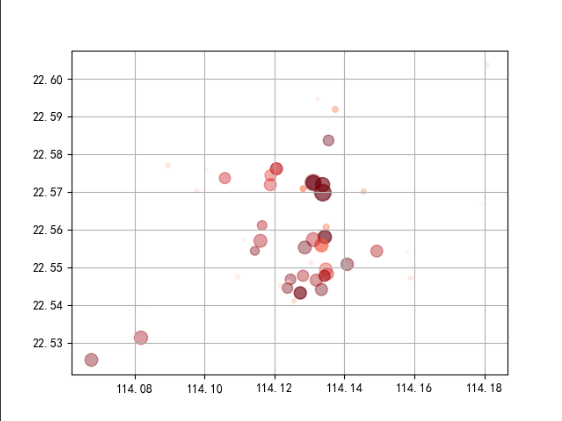
通过散点图大致看一下数据分布情况，如图1所示：

图1 颜色越深代表房价越高，经纬度可以确定深圳罗湖不同二手房的位置，从而表现出在不同位置二手房的房价。

# 极差
def d_range(df, *cols):
    krange = []
    for col in cols:
        crange = df[col].max() - df[col].min()
        krange.append(crange)
    return krange
key1 = '参考总价'
key2 = '参考首付'
dr = d_range(data, key1, key2)
print("%s极差为：%f\n%s极差为：%f" % (key1, dr[0], key2, dr[1]))

图2 计算结果如图所示。

# 频率分布情况
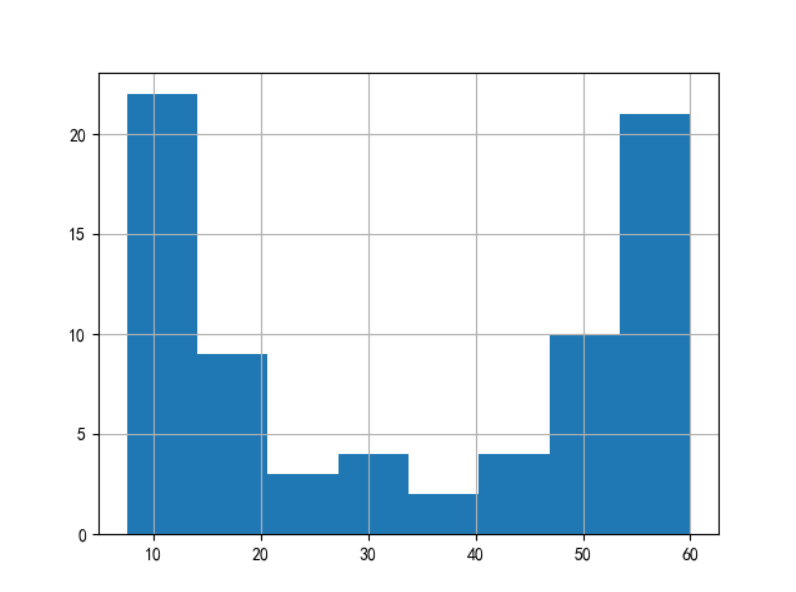
data[key2].hist(bins=8)
# 频数分布情况，分组区间
gcut = pd.cut(data[key1], 10, right=False)
gcut_count = gcut.value_counts(sort=False)
data1 = data['%s分组区间' % key1] = gcut.value_counts
# 区间出现频率
r_zj = pd.DataFrame(gcut_count)
r_zj.rename(columns={ 
   gcut_count.name: '频数'}, inplace=True)
r_zj['频率'] = r_zj['频数'] / r_zj['频数'].sum()
r_zj['累计频率'] = r_zj['频率'].cumsum()
r_zj['频率%'] = r_zj['频率'].apply(lambda x: "%.2f%%" % (x * 100))
r_zj['累计频率%'] = r_zj['累计频率'].apply(lambda x: "%.2f%%" % (x * 100))
r_zj.style.bar(subset=['频率', '累计频率'])
# 直方图
r_zj['频率'].plot(kind='bar', figsize=(12, 2),
                grid=True, color='k', alpha=0.4)
plt.show()

图3 通过直方图，我们可以看出不同区间二手房首付价格的大致分布情况。

对比分析

对比分析就是用两组或两组以上的数据进行比较，是最通用的方法。我们知道孤立的数据、图像没有意义，有对比才有差异。比如在时间维度上的同比和环比、增长率、定基比，与竞争对手的对比、类别之间的对比、特征和属性对比等。对比法可以发现数据变化规律，使用频繁，经常和其他方法搭配使用。该方法一般会结合其他方法在后文呈现，这里不加赘述。

统计分析

1、集中趋势度量：指一组数据向某一中心靠拢的倾向，核心在于寻找数据的代表值或者中心值————统计平均数
常用指标为： 算数平均数（均值）、位置平均数（中位数）、 众数
2、离中趋势量：指一组数据中各数据以不同程度的距离偏离中心的趋势。
常用指标为：极差、标准差

# 算数平均数
data = pd.DataFrame({ 
   'value': np.random.randint(100, 120, 100),
                     'f': np.random.rand(100)})
data['f'] = data['f'] / data['f'].sum()  # f为权重，这里将f列设置成总和为1的权重占比
mean = (data['value']*data['f'].sum()/data)

帕累托分析

帕累托分析（贡献度分析）即为我们常说的帕累托法则：20/80定律。“原因和结果、投入和产出、努力和报酬之间本来存在着无法解释的不平衡。一般来说，投入和努力可以分为两种不同的类型：
1、多数，它们只能造成少许的影响；
2、少数，它们造成主要的、重大的影响。”
比如说，一个公司80%利润来自于20%的畅销产品，而其他80%的产品只产生了20%的利润，通过二八原则，寻找关键的20%决定性因素！

# 获取数据
data = pd.Series(np.random.randn(10) * 1200 + 3000,
                 index=list('ABCDEFGHIJ'))
# 排序
data.sort_values(ascending=False, inplace=True)
# 画图
plt.figure(figsize=(10, 4))
fig = data.plot(kind='bar', color='g', alpha=0.8, width=0.6)
p = data.cumsum() / data.sum()
key = p[p > 0.8].index[0]
key_num = data.index.tolist().index(key)
# 找到累计占比超过80%时的index
# 找到key所对应的索引位置
# 输出决定性因素产品
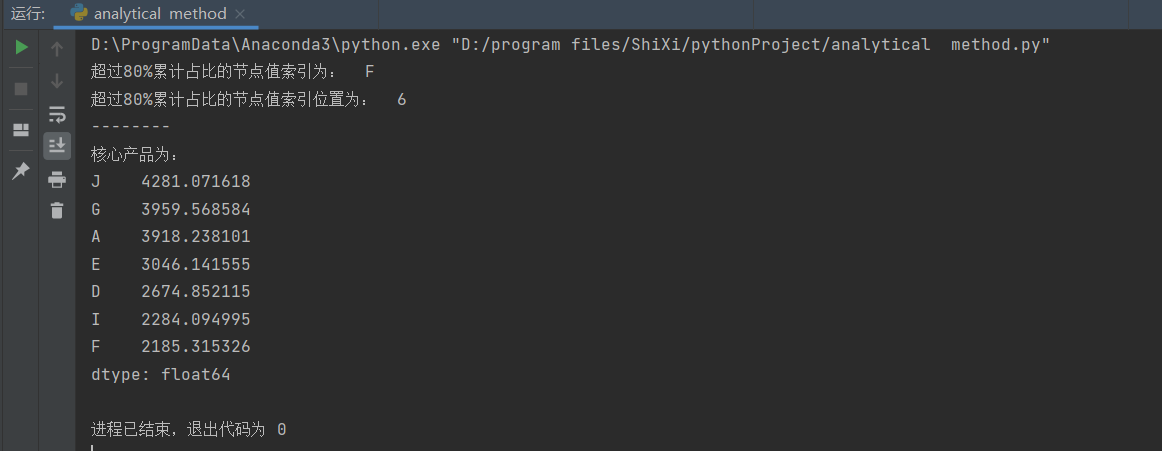
print('超过80%累计占比的节点值索引为： ', key)
print('超过80%累计占比的节点值索引位置为： ', key_num)

## 图像表示
p.plot(style='--ko', secondary_y=True)
plt.axvline(key_num, color='r', linestyle='--')
plt.text(key_num + 0.2, p[key], '累计占比为：%.3f%%' % (p[key] * 100), color='r')
plt.ylabel('营收比例')
# 绘制营收累计占比曲线
key_product = data.loc[:key]
print('核心产品为： ')
print(key_product)
plt.show()

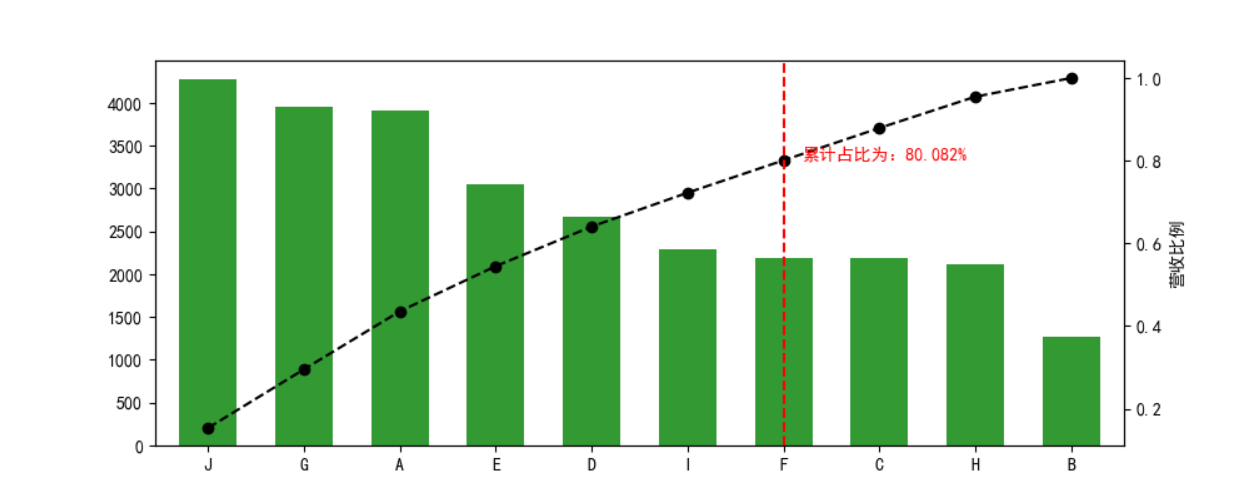
图4 即为帕累托可视化图像。J～F占所有种类的70％,贡献了80.082%的利润,企业应增加J-F的投入,减少Ｃ～Ｂ的投入以获得更高的盈利额。

图5 运行结果，通过结合图像可以很快地找到超过80%累计占比的节点以及对应的节点值。

正态性分析

正态性检验：
利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。

常用方法：直方图初判/QQ图判断/K-S检验

## 方法1：直方图
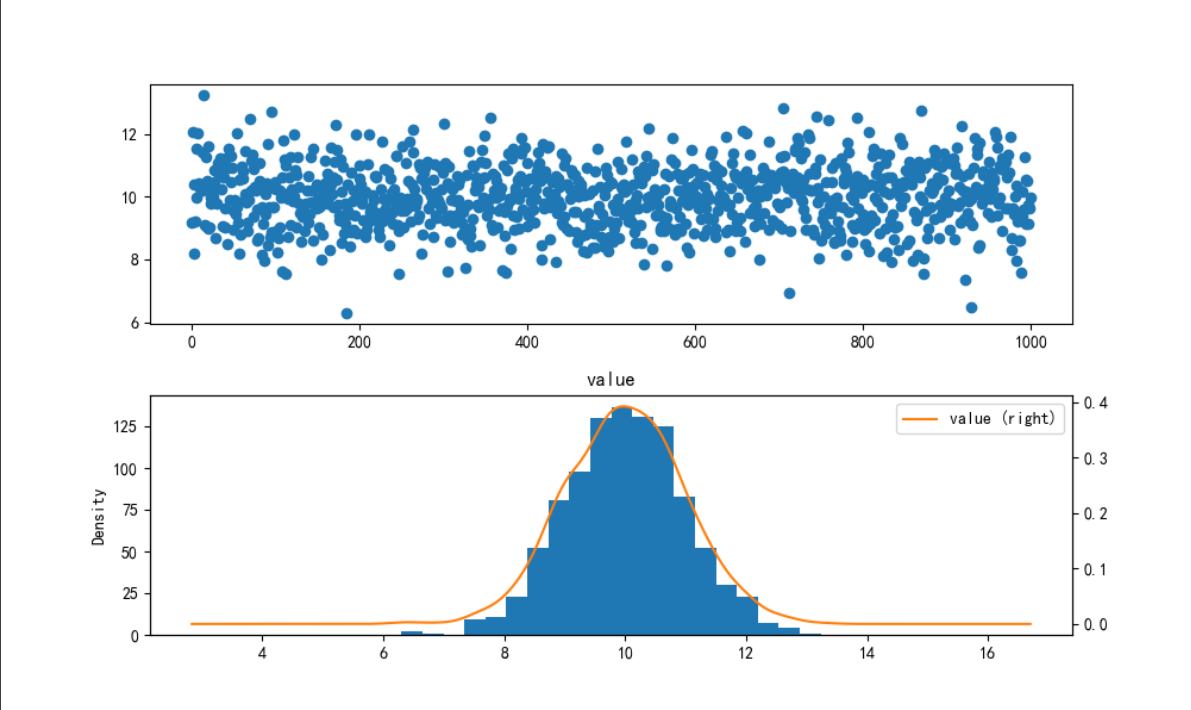
data = pd.DataFrame(np.random.randn(1000)+10, columns=['value'])
fig = plt.figure(figsize=(10, 6))
ax1 = fig.add_subplot(2, 1, 1)
ax1.scatter(data.index, data.values)

ax2 = fig.add_subplot(2, 1, 2)
data.hist(bins=20, ax=ax2)
data.plot(kind='kde', secondary_y=True, ax=ax2)
plt.show()

图6 第2个子图即为直方图。利用散点图和直方图，我们可以清晰地看出该组数据满足正态分布。

## 方法2：QQ图判断
# QQ图通过把测试样本数据的分位数与已知分布比较，从而检验数据的分布情况

'''
--元素--
QQ图是一种散点图，对应于正太分布的QQ图，就是由标准正太分布的分位数为横坐标，
样本值为纵坐标的散点图
参考元素：四分之一分位点和四分之三分位点这两点确定参考线，看散点是否分布在参考线附近。
--绘制思路--
1、在做好数据清洗后，对数据进行排序(此排序统计量：x(1)<x(2)<x(3)<...<x(n))
2、排序后，计算出每个数据对应的百分位p[i]，即第i个数据x(i)为p(i)的百分位
其中，p(i)=(i-0.5)/n
3、绘制直方图加QQ图，直方图作为参考
'''
data = pd.DataFrame(np.random.randn(1000)+10, columns=['value'])
mean = data['value'].mean()
std = data['value'].std()
print('均值为： %.2f,标准差为： %.2f' % (mean, std))

# 计算均值，标准差
data.sort_values(by='value', inplace=True) # 排序
data_re = data.reset_index(drop=False)
# 计算Q值，百分位
data_re['p'] = (data_re.index-0.5)/len(data_re)
data_re['q'] = (data_re['value']-mean)/std
st = data['value'].describe()
x1, y1 = 0.25, st['25%']
x2, y2 = 0.75, st['75%']
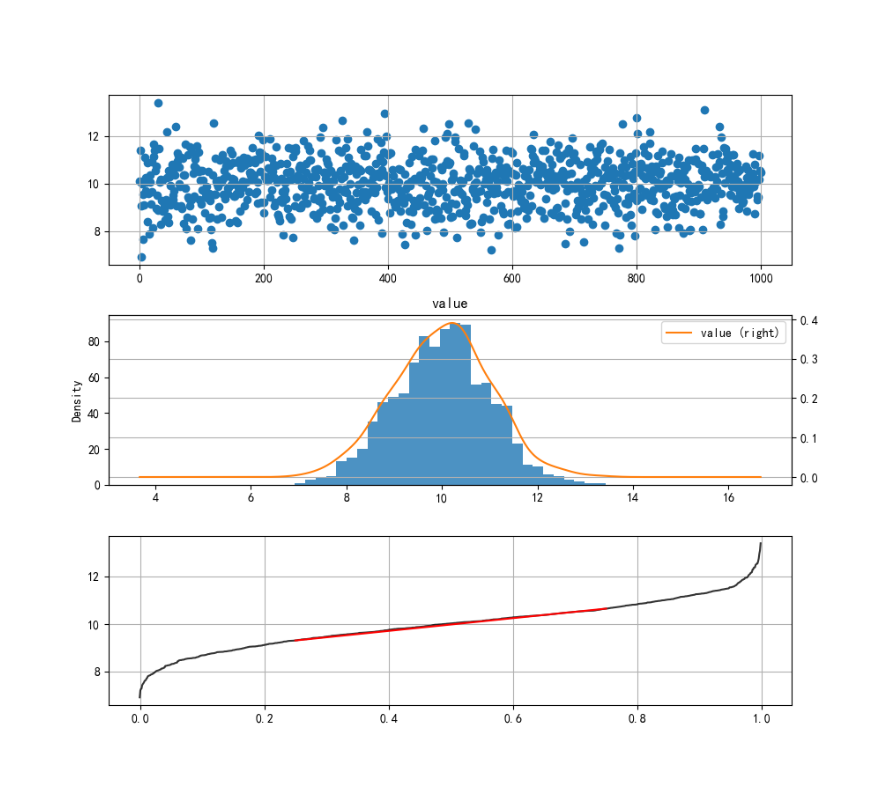
fig = plt.figure(figsize=(10, 9))
ax1 = fig.add_subplot(3, 1, 1)
ax1.scatter(data.index, data.values)
plt.grid()

# 绘制数据分布图
ax2 = fig.add_subplot(3, 1, 2)
data.hist(bins=30, alpha=0.8, ax=ax2)
data.plot(kind='kde', secondary_y=True, ax=ax2)
plt.grid()

ax3 = fig.add_subplot(3, 1, 3)
ax3.plot(data_re['p'], data_re['value'], 'k', alpha=0.8)
ax3.plot([x1, x2], [y1, y2], '-r')
plt.grid()
plt.show()

图7 第3个子图即为QQ图。利用不同图像的对比分析，我们可以清晰地看出QQ图通过分位点的方式可以很好表现出正态分布特征。

'''
＃＃　方法3：K-S检验（Kolmogorov-Smirnov）是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。
以样本数据的累计频数分布与特定的理论分布比较（如正态分布），如果两者差距小，则推论样本分布取自某特定分布。

假设检验问题：
H0：样本的总体分布服从某特定分布
H1：样本的总体分布不服从某特定分布

Fn(x)->样本的累计分布函数
F0(x)->理论分布的分布函数
D->F0(x)与Fn(x)差值的绝对值最大值
D = max|Fn(x)-F0(x)|

D > D(n,a)相比较->
p>0.05则接受H0,p<0.05则拒绝H0，接受H1。
'''
# 直接用算法做KS检验
from scipy import stats
# 样本数据是35位健康男性在未进食之前的血糖浓度
data = [87, 77, 92, 68, 80, 78, 84, 77, 81, 80, 80, 77, 92, 86,
        76, 80, 81, 75, 77, 72, 81, 72, 84, 86, 80, 68, 77, 87,
        76, 77, 78, 92, 75, 80, 78]
df = pd.DataFrame(data, columns=['value'])
u = df['value'].mean()
std = df['value'].std()
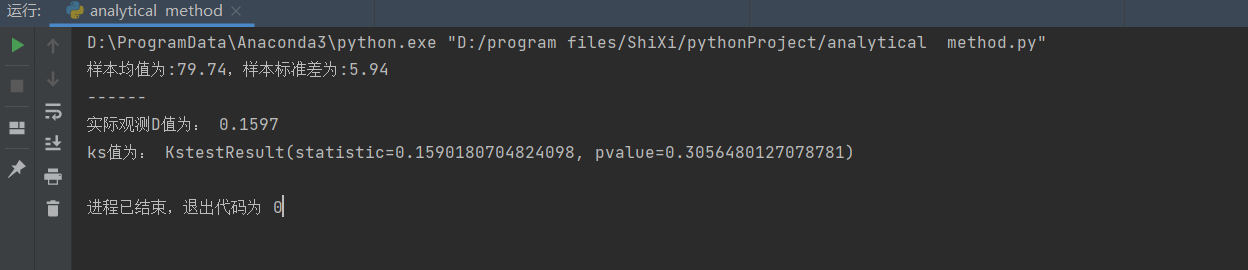
print("样本均值为:%.2f，样本标准差为:%.2f " % (u, std))
print("------")
# KS 方法：ks检验，参数分别是：待检验的数据，检验方法（norm 即正态分布），均值和标准差
# 返回两个值：static->D值，pvalue->P值
# p大于0.05时为正态分布
s = df['value'].value_counts().sort_index()
df_s = pd.DataFrame({ 
   '血糖浓度': s.index, '次数': s.values})
df_s['累计次数'] = df_s['次数'].cumsum()
df_s['累计频率'] = df_s['累计次数'] / len(data)
df_s['标准化取值'] = (df_s['血糖浓度'] - u) / std
# 查表得到理论分布数值
df_s['理论分布'] = [0.0244, 0.0968, 0.2148, 0.2643, 0.3228, 0.3859, 0.5160, 0.5832, 0.7611, 0.8531, 0.8888, 0.9803]
df_s['D'] = np.abs(df_s['累计频率'] - df_s['理论分布'])
dmax = df_s['D'].max()
print("实际观测D值为： %.4f" % dmax)
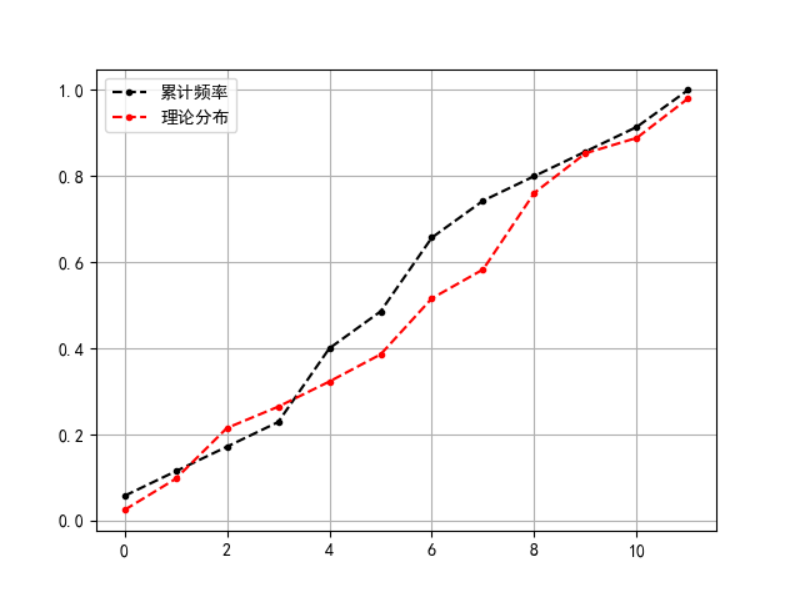
df_s['累计频率'].plot(style='--k.')
df_s['理论分布'].plot(style='--r.')
plt.legend(loc='upper left')
plt.grid()
plt.show()

图8 通过理论推导得出的结果如图所示。

ks = stats.kstest(df['value'], 'norm', (u, std))
print("ks值为：", ks)

图9 但在scipy包种有该正态分布检验方法，即ks代码块儿。

相关性分析

相关性分析：是指对两个或者多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度，且相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。

图示判断：
Pearson相关系数（皮尔逊相关系数）
Sperman秩相关系数（斯皮尔曼相关系数）

## （1）两个变量之间的线性相关性
# 创建三个数据：data1为0-100的随机数并从小到大排序，data2为0-50的随机数并从小到大排序，data3为0-500的随机数并从大到小排序
data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending=False)

fig = plt.figure(figsize=(10, 4))
ax1 = fig.add_subplot(1, 2, 1)
ax1.scatter(data1, data2)  # 正相关
plt.grid()

ax2 = fig.add_subplot(1, 2, 2)
ax2.scatter(data1, data3)  # 负相关
plt.grid()

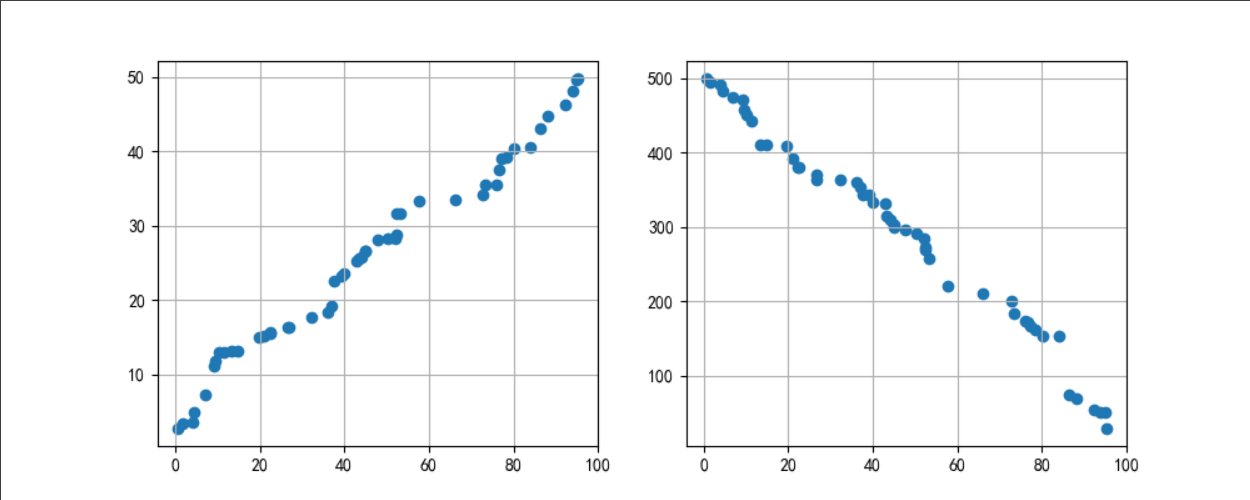
图10 左图为正相关，右图为负相关。

##（2）散点图矩阵判断多变量间关系
data = pd.DataFrame(np.random.randn(200, 4) * 100, columns=['A', 'B', 'C', 'D'])
pd.plotting.scatter_matrix(data, figsize=(8, 8),
                           color='k',marker='+',
                           diagonal='hist', alpha=0.8,                   
                           range_padding=0.1)
data.head()
plt.show()

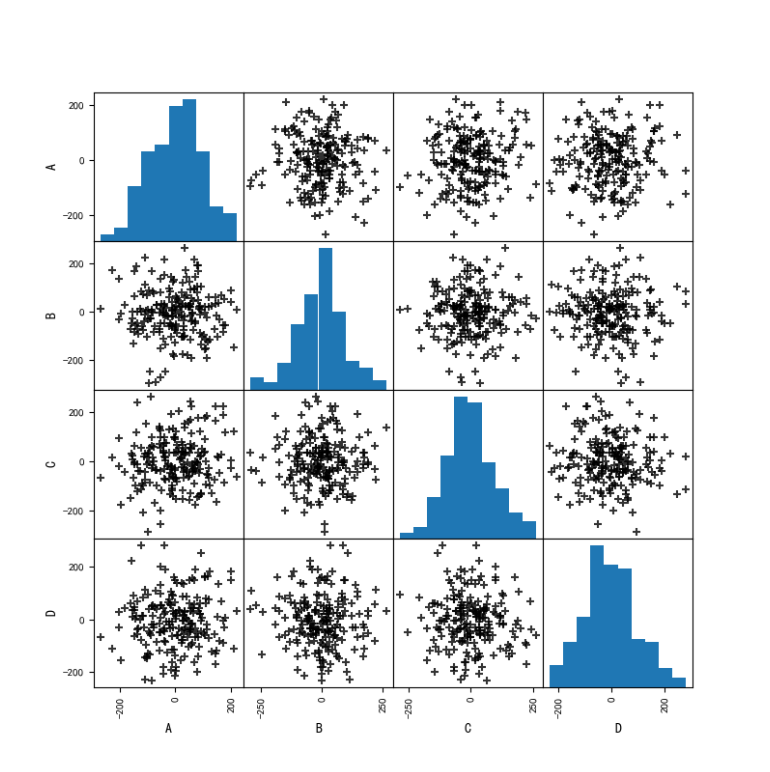
图11 多变量之间可以用散点矩阵图，但该数据无法看出不同变量之间的相关性。
以上皆为通过图像来判断数据相关性的方法，我们还可以通过数据的方式来判断不同变量之间的相关性。

'''
皮尔逊相关系数：即皮尔森积矩相关系数，是一种线性相关系数。
可以衡量向量相似度的一种方法》输出范围为-1到+1，0代表无相关性，负值代表负相关，正值代表正相关。
0<|r|<1代表存在不同程度线性相关
》 |r|<=0.3  -->不存在线性相关
》 |r|<=0.5  -->低度线性相关
》 |r|<=0.8  -->显著线性相关
》 |r|> 0.8  -->高度线性相关

前提条件 --> 正态分布
'''
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({ 
   'value1': data1.values,
                     'value2': data2.values})
# 检验是否满足正态分布
u1, u2 = data['value1'].mean(), data['value2'].mean()
std1, std2 = data['value1'].std(), data['value2'].std()
print('value1正正态检验：\n', stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正正态检验：\n', stats.kstest(data['value2'], 'norm', (u2, std2)))

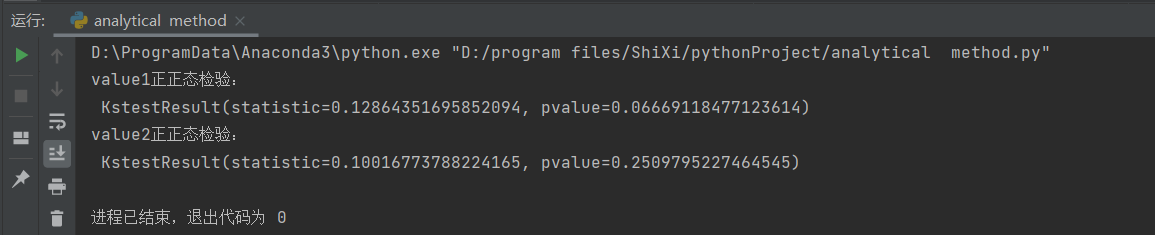
图12 pvalue均大于0.05，则满足正态分布。

## 计算Pearson相关系数
data['(x-u1)*(y-u2)'] = (data['value1']-u1)*(data['value2']-u2)
data['(x-u1)**2'] = (data['value1']-u1)**2
data['(y-u2)**2'] = (data['value2']-u2)**2
r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print("Pearson相关系数为：%.4f" % r)

# 等价于下列代码
p = data.corr()
print(p)

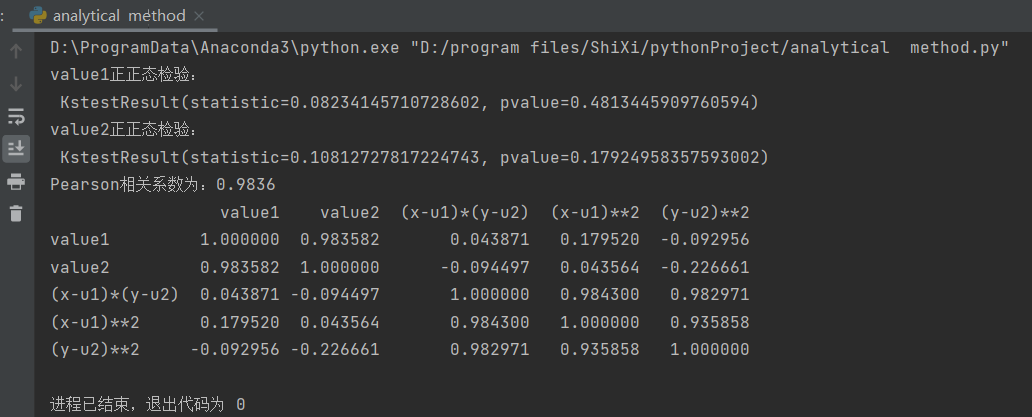
图13 通过推导得出相关系数和导入函数包结果对比如图所示。由计算出的结果大于0.05，我们可以看出该组数据存在相关性。
然而，Pearson相关系数主要用于服从正态分布的连续变量，不服从正态分布的变量、分类的关联性可采用Sperman秩关联系数，也称等级相关系数。
计算逻辑：
（1）对两个变量成对的取值按照从小到大顺序编秩，Rx代表Xi的秩次， Ry代表Yi的秩次，如果两个值大小一样，则秩次为（index1 + index2） / 2；
（2）di = Rx – Ry
Spearson系数和Pearson 系数在效率上等效

# 判断看电视和智商的相关性
data = pd.DataFrame({ 
   '智商': [106, 86, 100, 101, 99, 103, 97, 113, 112, 110],
                     '每周看电视小时数': [7, 0, 27, 50, 28, 29, 20, 12, 6, 17]})
data.sort_values('智商', inplace=True)
n = len(data)
data['range1'] = np.arange(1, n+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1, n+1)
data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2
rs = 1-6*(data['d2'].sum()) / (n * (n**2-1))
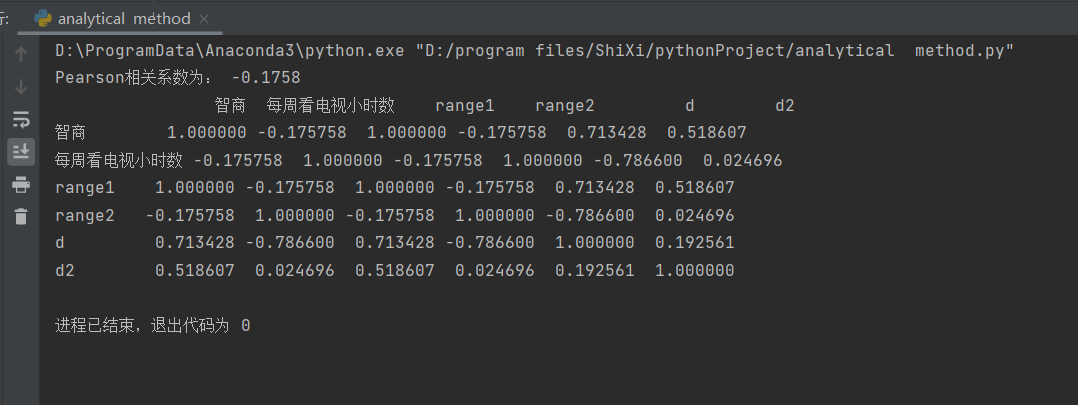
print('Pearson相关系数为： %.4f' % rs)

# 以上皆为利用公式推导结果，等价于以下代码
s = data.corr(method='spearman')
print(s)

图14 结果为负值，代表看电视和智商并不相关。

总结

以上就是今天需要总结的数据特征方法。但是我们需要清楚地知道，在实际案例中，我们需要结合不同的方法科学地分析不同数据蕴含的数据特征。在相关性分析当中，还有几种分别kendall（和谐系数）和GRA（GreyRelationAnalysis，GRA）灰色关联度分析，以及几个重要性分析（MDI、MDA）后期再更。

今天的文章数据特征分析方法总结怎么写_定量分析的基本步骤分享到此就结束了，感谢您的阅读。