矩阵范数怎么求_矩阵范数怎么求「建议收藏」

本文内容

可能你在某个地方听说了einsum，然后不会写，或者看不懂。这篇文章将会一步一步教会你如何使用（通法哦，只要学会方法就全会了）。

Einsum函数简介

ein 就是爱因斯坦的ein，sum就是求和。einsum就是爱因斯坦求和约定，其实作用就是把求和符号省略，就这么简单。举个例子：

我们现在有一个矩阵

$$A_{2\times 2}=\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)$$

我们想对A的“行”进行求和得到矩阵B(向量B)，用公式表示，则为：

$$B_i=\sum _j{A}_{ij}=B_2=\left(\begin{array}{c}3\\ 7\end{array}\right)$$

对于这个求和符号，爱因斯坦说看着有点多余，要不就省略了吧，然后式子就变成了:

$$B_i=A_{ij}$$

用einsum表示呢，则为: torch.einsum("ij->i", A)。->符号就相当于等号，->左边的ij就相当于$A_{ij}$,->右边的i就相当于$B_i$。einsum接收的第一个参数为einsum表达式，后面的参数为等号右边的矩阵。

不只是pytorch里有，numpy，tensonflow这些里面都有einsum。
这里的$i,j$是指代A的下标，也可以换成其他字母

到这里，如果悟性好的同学应该就已经彻底懂了。但应该还有很多同学和我一样处于懵逼状态，所以接下来我会讲解如何看懂一个einsum公式和如何写出einsum表达式。

如何看懂一个einsum式子

当我们拿到一个einsum表达式后，第一步是要写出它的数学表达式。例如，我们有如下一个einsum表达式：

A = torch.Tensor(range(2*3*4)).view(2, 3, 4)
C = torch.einsum("ijk->jk", A)

则，该式子的数学表达式为：

$$C_{jk}=A_{ijk}$$

第二步，补充$\sum$符号，那如何补，补几个，$\sum$下面放什么呢？这里就要看左右两边下标的差异了，要补的$\sum$符号就是右边的下标减左边的下标。在这个例子中，右边有$ijk$，而左边是$jk$，差了一个$i$，所以补${\sum }_i$。最终为：

$$C_{jk}=\sum _i{A}_{ijk}$$

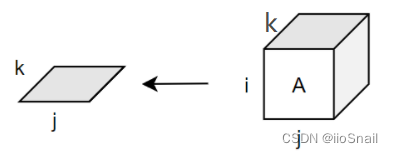
第三步，用笔纸画出（或脑补出）这个等式到底干了些啥，对于该等式，可以画为：

这样就可以很容易看出来，它是将$i$行都给加一起了，等价于 C = A.sum(dim=0)

第四步，尝试用for循环复现，其实einsum还是很好复现的，就按照公式写for循环就行了，求和的部分用+=

i, j, k = A.shape[0], A.shape[1], A.shape[2] # 得到 i, j, k
C_ = torch.zeros(j, k) # 初始化 C_ , 用来保存结果
for i_ in range(i): # 遍历 i
    for k_ in range(k): # 遍历 j
        for j_ in range(j): # 遍历 k
            C_[j_][k_] += A[i_][j_][k_] # 求和

C, C_

(tensor([[12., 14., 16., 18.],
         [20., 22., 24., 26.],
         [28., 30., 32., 34.]]),
 tensor([[12., 14., 16., 18.],
         [20., 22., 24., 26.],
         [28., 30., 32., 34.]]))

可以看到，我们的for循环结果和einsum的结果一致。

到这里，如何看懂einsum就结束了，按照上面四步走，多加练习即可。

如何看懂一个einsum式子（实战）

我也练几个。先来一个简单的。

A = torch.Tensor(range(2*3)).view(2, 3)
B = torch.einsum("ij->ji", A)

第一步，写出数学表达式：

$$B_{ji}=A_{ij}$$

第二步，添加$\sum$符号，这里左边是$ji$，右边是$ij$，不多不少，正正好，所以不需要（也不能）增添$\sum$符号。

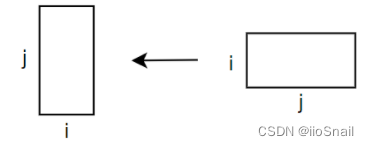
第三步，画出矩阵的变换过程：

哦，这不就是求转置矩阵嘛。

第四步，使用for循环复现：

i, j = A.shape[0], A.shape[1] # 得到 i, j
B_ = torch.zeros(j, i) # 初始化 B_ , 用来保存结果
for i_ in range(i): # 遍历 i
    for j_ in range(j): # 遍历 j
        B_[j_][i_] = A[i_][j_]  # 因为不需要求和，所以这里用=，而不是+=“”

B, B_

(tensor([[0., 3.],
         [1., 4.],
         [2., 5.]]),
 tensor([[0., 3.],
         [1., 4.],
         [2., 5.]]))

接下来来个难的。

A = torch.Tensor(range(2*3*4*5)).view(2, 3, 4, 5)
B = torch.Tensor(range(2*3*7*8)).view(2, 3, 7, 8)
C = torch.einsum("ijkl,ijmn->klmn", A, B)

如果等式右边有多个矩阵，则用逗号分割。

第一步，写出数学表达式：

$$C_{klmn}=A_{ijkl}{B}_{ijmn}$$

第二步，补充求和符号，右边有$ijklmn$,左边有$klmn$，左边少了$ij$，所以补两个求和符号，即${\sum }_i{\sum }_j$。最终为：

$$C_{klmn}=\sum _i\sum _j{A}_{ijkl}{B}_{ijmn}$$

注意这里$A_{ijkl}{B}_{ijmn}$可不是矩阵相乘，而是两个数字相乘，因为$A_{ijkl}$和$B_{ijmn}$都是数字

第三步，画出矩阵变换过程。四维太难画了，脑补吧。

第四步，使用for循环进行复现。

i,j,k,l,m,n = A.shape[0],A.shape[1],A.shape[2],A.shape[3],B.shape[2],B.shape[3]
C_ = torch.zeros(k,l,m,n)
for i_ in range(i):
    for j_ in range(j):
        for k_ in range(k):
            for l_ in range(l):
                for m_ in range(m):
                    for n_ in range(n):
                        # 由于有求和符号，所以用+=
                        C_[k_][l_][m_][n_] += A[i_][j_][k_][l_]*B[i_][j_][m_][n_]

C == C_

tensor([[[[True, True, True,  ..., True, True, True],
		  ...........................
          [True, True, True,  ..., True, True, True]]]])

einsum特殊写法补充

1. 若等号左边就是一个数，那么->左边什么都不用写，例如：

$$b=\sum _{ijk}{A}_{ijk}$$

A = torch.Tensor(range(1*2*3)).view(1, 2, 3)
b = torch.einsum("ijk->", A) # 由于b是一个数，没有下标，所以->右边什么都不用写
b

tensor(15.)

2. 若下标过多，或不确定，则可以省略，例如：

$$B_{\ast }=\sum _i{A}_{i\ast }$$

A = torch.Tensor(range(1*2*3)).view(1, 2, 3)
B = torch.einsum("i...->...", A)  # 省略号表示*
B.size()

torch.Size([2, 3])

目前为止，你应该可以看得懂einsum表达式了，若看不懂，大概率是因为公式的问题，确实有些求和公式很复杂，你可以慢慢拆解求和公式，看看具体表示的什么含义。

如何写出einsum表达式

要写出einsum表达式也很简单，只要将上面的步骤反过来就行了，①先画出你要做的矩阵运算；②尝试用for循环实现；③写出数学表达式；④写出einsum表达式，并验证。

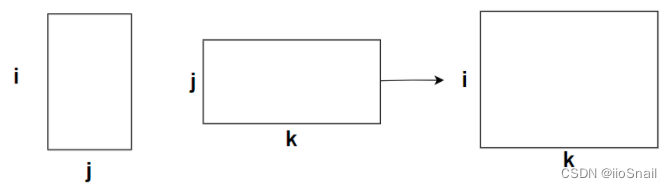
接下来，我们用矩阵相乘公式来进行演示。第一步，我们要画出矩阵相乘的操作过程，如下：

第二步，尝试使用for循环实现：

A = torch.Tensor(range(2*3)).view(2, 3)
B = torch.Tensor(range(3*4)).view(3, 4)
C = torch.zeros(i, k)
i, j, k = 2, 3, 4
for i_ in range(i):
    for j_ in range(j):
        for k_ in range(k):
            C[i_][k_] += A[i_][j_]*B[j_][k_]

第三步，写出数学表达式：

$$C_{ik}=A_{ij}{B}_{jk}$$

第3.2步，补充求和符号，左边是$ik$，右边是$ijk$，少了$j$，补${\sum }_j$：

$$C_{ik}=\sum _j{A}_{ij}{B}_{jk}$$

第四步，写出einsum表达式并验证：

D = torch.einsum("ij,jk->ik", A, B) 
E = A@B

C, D, E

(tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]),
 tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]),
 tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]))

参考资料：

einsum is all you need: https://www.youtube.com/watch?v=pkVwUVEHmfI

今天的文章矩阵范数怎么求_矩阵范数怎么求「建议收藏」分享到此就结束了，感谢您的阅读。