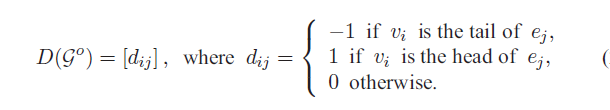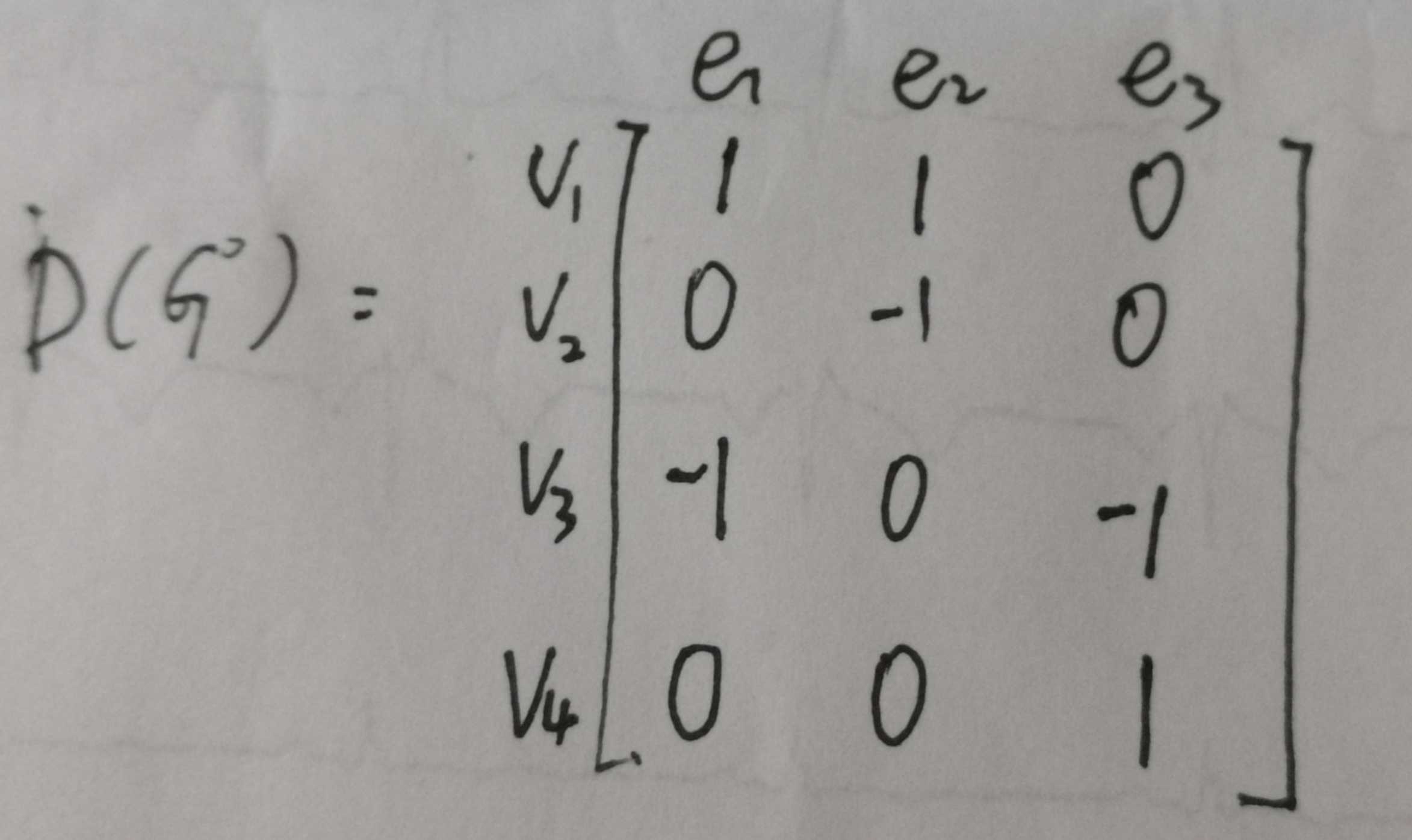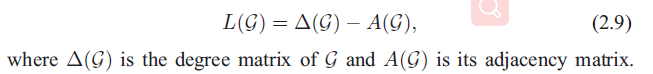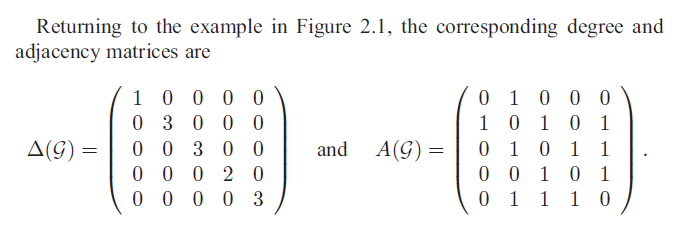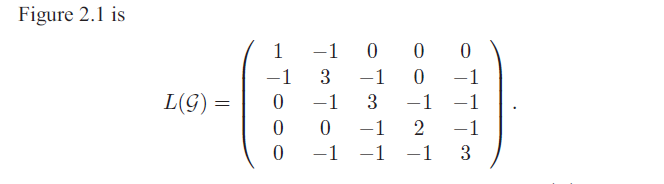拉普拉斯矩阵与关联矩阵公式_拉普拉斯行列式

前言

      本文介绍了一些图论的基础知识，包括图的关联矩阵、拉普拉斯矩阵，其中只考虑无自环的情况，本文中某些图片或者知识的参考/来源已列于本文最后。图、邻居、度矩阵、邻接矩阵参考另一篇博客图的一些基本知识：关联矩阵、拉普拉斯矩阵

关联矩阵（Incidence Matrix）

      关联矩阵是n×m的矩阵，n为顶点数量，m为边数量。
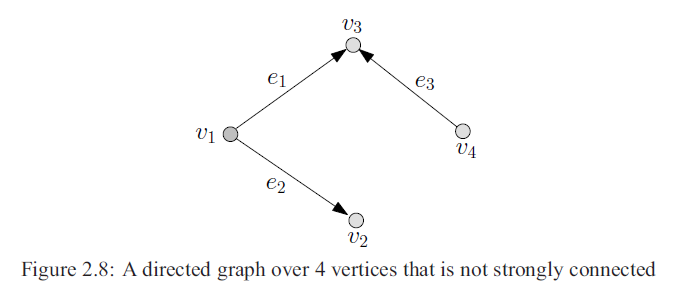
      对于有向图，关联矩阵如下，其中若顶点在边的起点，则 dij=1；若顶点在边的终点，则 dij=-1；其他 dij=0。

      对于无向图，关联矩阵中，顶点只要在边上，则dij=1；其他 dij=0。

有向图举例

     有向图关联矩阵特点：

• 每一列只有两个非零元素，一个是+1，一个是-1，关联矩阵每一列元素之和为零。
• 矩阵中任一行可以从其他 n-1 行中导出，即只有 n-1 行是独立的。

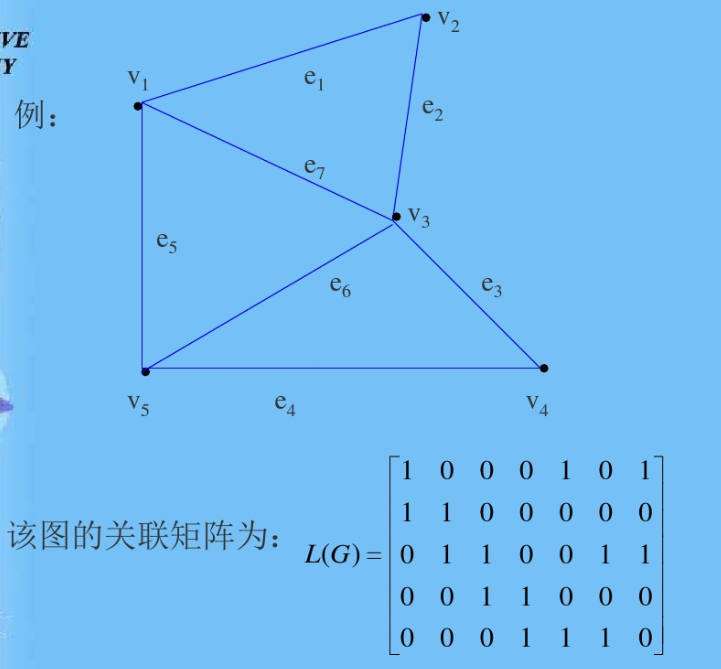
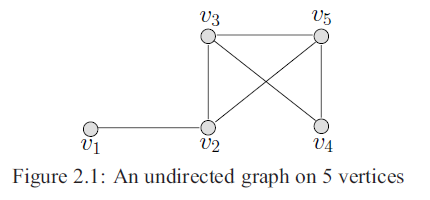
无向图举例

      无向图关联矩阵特点:

• 因为每条边关联于两个顶点，所以关联矩阵每一列有且只有两个1
• 关联矩阵的每一行种的所有元素之和对应于此行顶点的度
• 若某一行所有的元素都为0，则此行对应的顶点为孤立点
• 重边所对应的列元素完全相同

拉普拉斯矩阵（Laplacian）

      拉普拉斯矩阵 = 度矩阵 – 邻接矩阵，其中有向图度矩阵根据应用情况使用出度矩阵或者入度矩阵。

举例说明

该无向图的度矩阵&邻接矩阵：

该无向图的拉普拉斯矩阵：

      拉普拉斯矩阵性质：

• 拉普拉斯矩阵是半正定矩阵；
• 特征值中0出现的次数就是图连通区域的个数；
• 最小特征值是0，对应的特征向量为全1列向量，因为拉普拉斯矩阵每一行的和均为0；
• 每一行的行和为0；

参考文献

[1] Mesbahi M, Egerstedt M. Graph theoretic methods in multiagent networks[M]. Princeton University Press, 2010.
[2] https://wenku.baidu.com/view/88172a8f09a1284ac850ad02de80d4d8d05a0158.html
[3] https://wenku.baidu.com/view/9476691f2e60ddccda38376baf1ffc4ffe47e232.html

今天的文章拉普拉斯矩阵与关联矩阵公式_拉普拉斯行列式分享到此就结束了，感谢您的阅读。