时间序列模型_建立时间序列模型的步骤

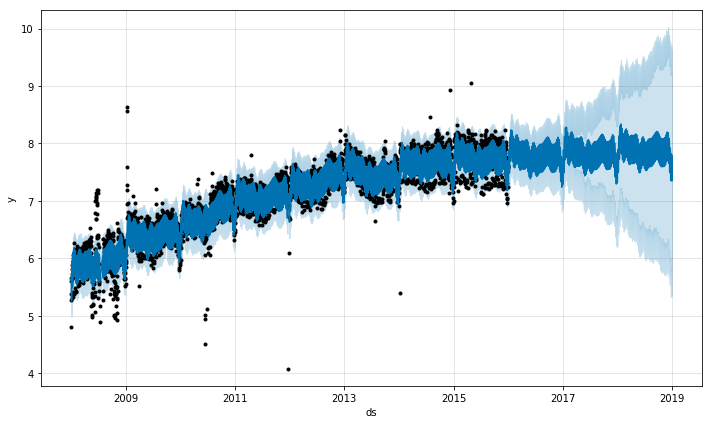
下面实例中使用的是佩顿 · 曼宁的维基百科主页每日访问量的时间序列数据（2007/12/10 – 2016/01/20）。我们使用 R 中的 Wikipediatrend 包获取该数据集。这个数据集具有多季节周期性、不断变化的增长率和可以拟合特定日期（例如佩顿 · 曼宁的决赛和超级碗）的情况等 Prophet 适用的性质，因此可以作为一个不错的例子。（注：佩顿 · 曼宁为前美式橄榄球四分卫）

首先，我们导入数据，该数据已经做过了log处理（即，做过df[‘y’] = np.log(df[‘y’])操作）。

# Python
import pandas as pd
from fbprophet import Prophet
# 读入数据集
df = pd.read_csv('examples/example_wp_log_peyton_manning.csv')
df.head()

1_1

通过对一个 Prophet 对象进行实例化来拟合模型，任何影响预测过程的设置都将在构造模型时被指定。接下来，就可以使用 fit 方法代入历史数据集来拟合模型，拟合过程应当花费 1 – 5 秒。

# 拟合模型
m = Prophet()
m.fit(df)

预测过程则需要建立在包含日期 ds 列的数据框基础上。通过使用辅助的方法 Prophet.make_future_dataframe 来将未来的日期扩展指定的天数，得到一个合规的数据框。默认情况下，这样做会自动包含历史数据的日期，因此我们也可以用来查看模型对于历史数据的拟合效果。

# 构建待预测日期数据框，periods = 365 代表除历史数据的日期外再往后推 365 天
future = m.make_future_dataframe(periods=365)
future.tail()

predict 方法将会对每一行未来 future 日期得到一个预测值（称为 yhat ）。如果你传入了历史数据的日期，它将会提供样本的模型拟合值。预测 forecast 创建的对象应当是一个新的数据框，其中包含一列预测值 yhat ，以及成分的分析和置信区间。

# 预测数据集
forecast = m.predict(future)
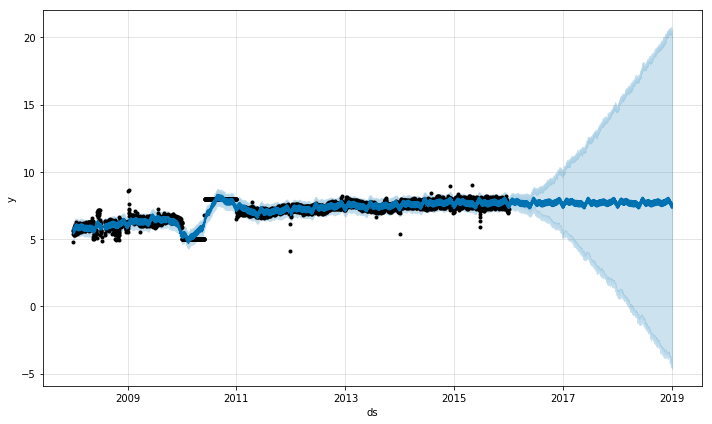
forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail()

通过 Prophet.plot 方法传入预测得到的数据框，可以对预测的效果进行绘图。

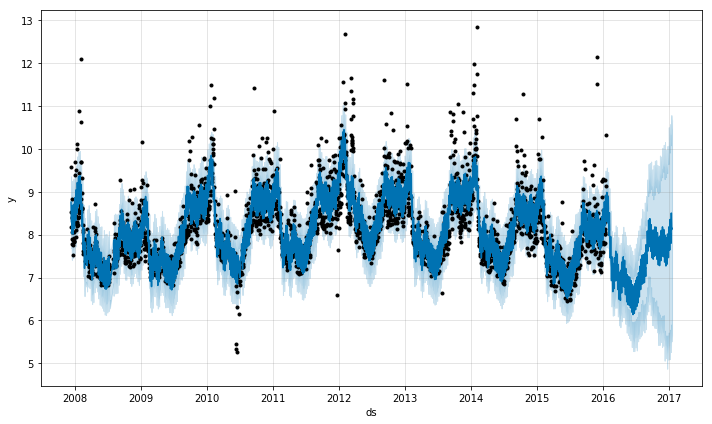
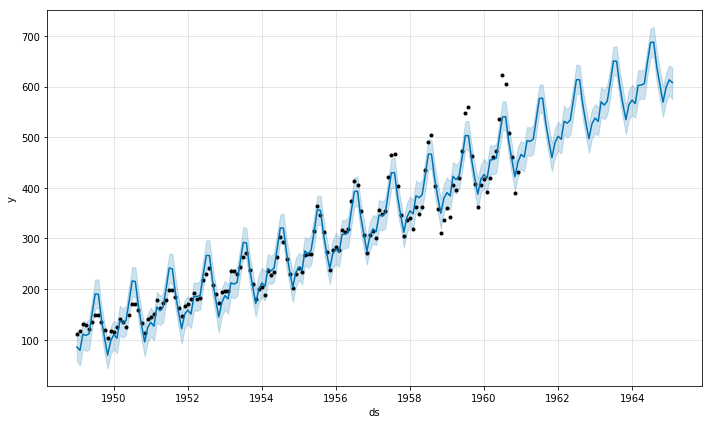
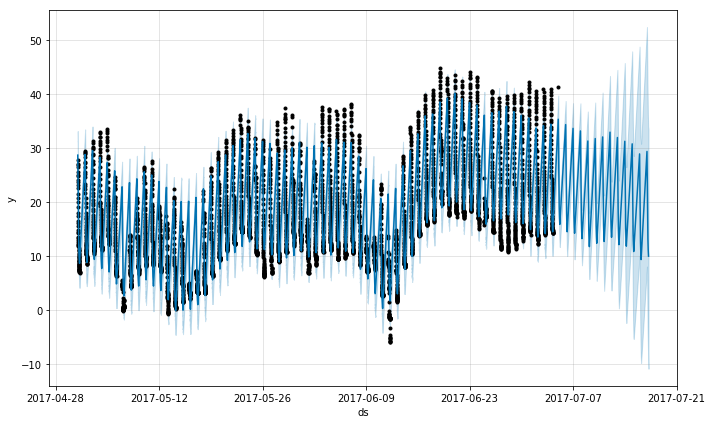
# 展示预测结果
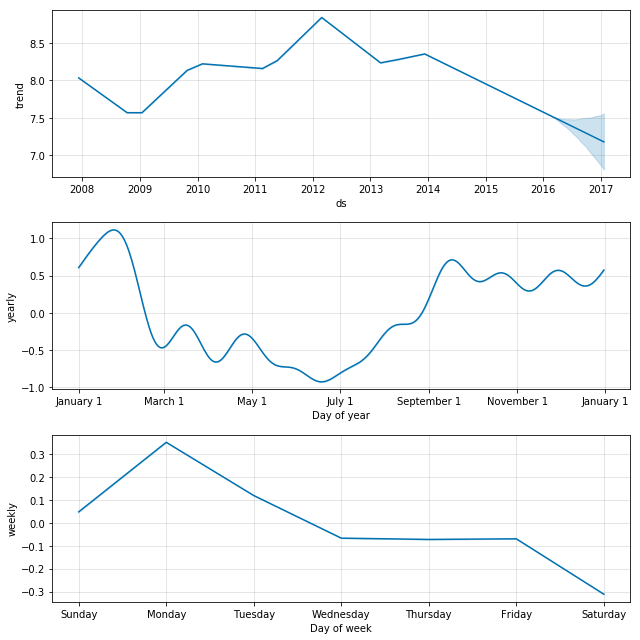
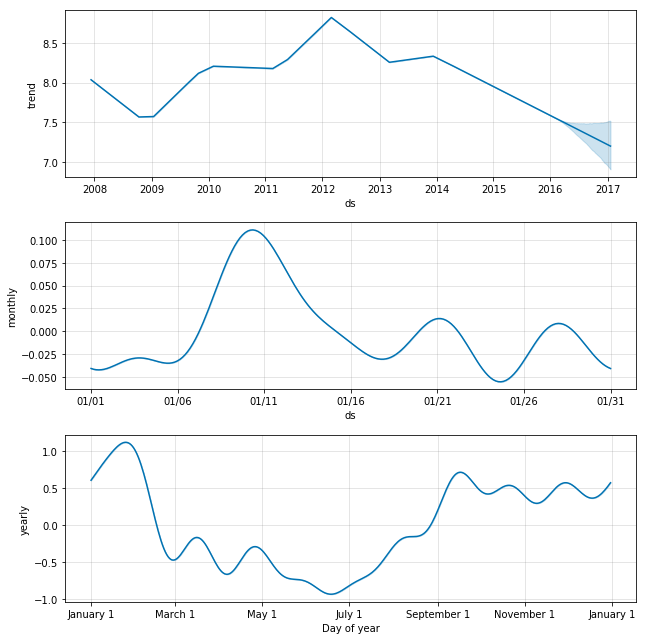
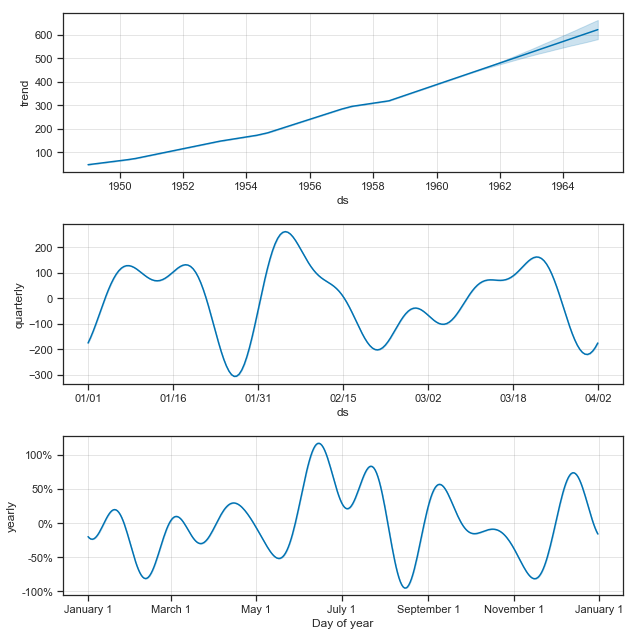
m.plot(forecast);

如果想查看预测的成分分析，可以使用 Prophet.plot_components 方法。默认情况下，将展示趋势、时间序列的年度季节性和周季节性。如果之前包含了节假日，也会展示出来。

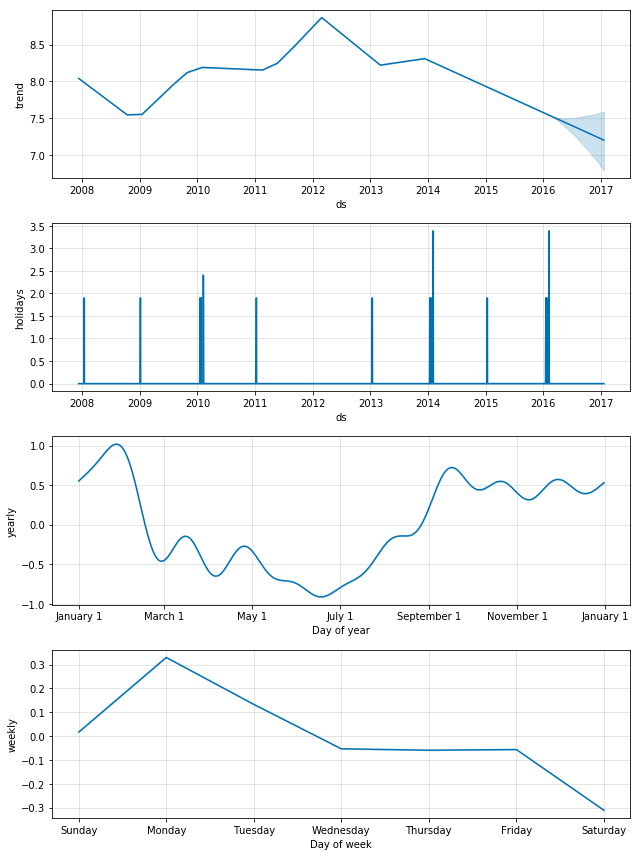
# 预测的成分分析绘图，展示预测中的趋势、周效应和年度效应
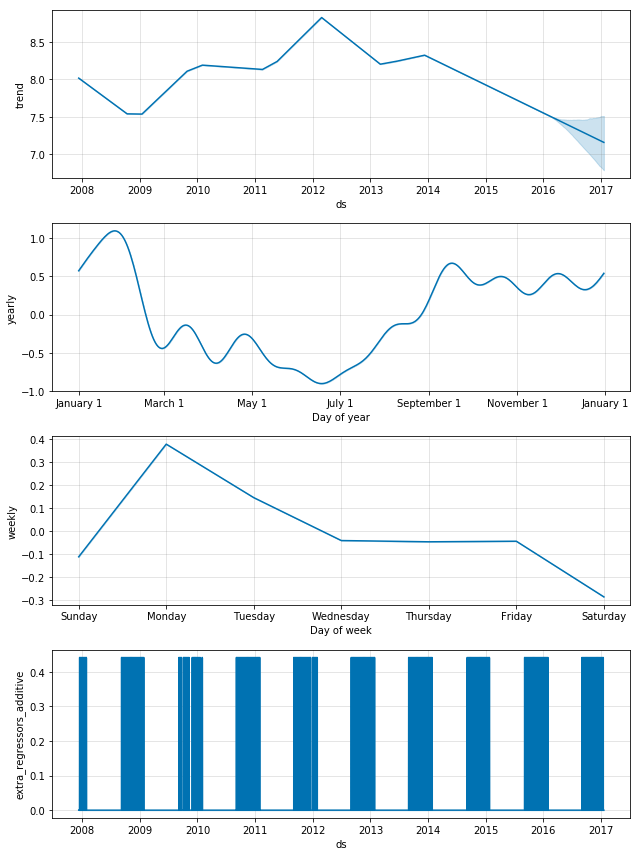
m.plot_components(forecast);

注：一个很核心的问题是我们应该怎么样理解上图的3个子图。通过对forecast这个Dataframe分析我们就可以得到结论。

我们先看下forecast都有哪些列。

print(forecast.columns)
Index(['ds', 'trend', 'trend_lower', 'trend_upper', 'yhat_lower', 'yhat_upper',
       'additive_terms', 'additive_terms_lower', 'additive_terms_upper',
       'multiplicative_terms', 'multiplicative_terms_lower',
       'multiplicative_terms_upper', 'weekly', 'weekly_lower', 'weekly_upper',
       'yearly', 'yearly_lower', 'yearly_upper', 'yhat'],
      dtype='object')

通过对数据的分析，我们就可以知道：

①图1是根据trend画出来的，图2是根据weekly画出来的，图3是根据yearly画出来的。

②因为是加法模型，有：forecast[‘additive_terms’] = forecast[‘weekly’] + forecast[‘yearly’]；有：forecast[‘yhat’] = forecast[‘trend’] + forecast[‘additive_terms’] 。因此：forecast[‘yhat’] = forecast[‘trend’] +forecast[‘weekly’] + forecast[‘yearly’]。

如果有节假日因素，那么就会有forecast[‘yhat’] = forecast[‘trend’] +forecast[‘weekly’] + forecast[‘yearly’] + forecast[‘holidays’]。

在第四部分，我们会讲到节假日因素，对于那些是节假日的天数，forecast[‘holidays’]才会有值，不是节假日的天数，forecast[‘holidays’]为0。

③因为是加法模型，’multiplicative_terms’, ‘multiplicative_terms_lower’, ‘multiplicative_terms_upper’这3列为空。

因此，基于上面的分析，weekly中的Monday为0.3的意思就是，在trend的基础上，加0.3；Saturday为-0.3的意思就是，在trend的基础上，减0.3。因此，这条线的高低也在一定程度上反应了“销量的趋势“。

注：许多方法的细节可以通过help(Prophet) 或者 help(Prophet.fit) 来获得。

二、饱和预测

2.1 预测饱和增长

默认情况下， Prophet 使用线性模型进行预测。当预测增长情况时，通常会存在可到达的最大极限值，例如：总市场规模、总人口数等等。这被称做承载能力（carrying capacity），那么预测时就应当在接近该值时趋于饱和。

Prophet 可使用 logistic 增长趋势模型进行预测，同时指定承载能力。下面使用 R 语言的维基百科主页访问量（取对数）的实例来进行说明。

首先，我们导入数据，该数据已经做过了log处理（即，做过df[‘y’] = np.log(df[‘y’])操作）。

import pandas as pd
from fbprophet import Prophet
df = pd.read_csv('examples/example_wp_log_R.csv')

新建一列 cap 来指定承载能力的大小。本实例中假设取某个特定的值，通常情况下这个值应当通过市场规模的数据或专业知识来决定。

df['cap'] = 8.5

值得注意的是数据框的每行都必须指定 cap 的值，但并非需要是恒定值。如果市场规模在不断地增长，那么 cap 也可以是不断增长的序列。

如之前教程所述来拟合模型，并且通过一个新增的参数来指定采用 logistic 增长：

m = Prophet(growth='logistic')
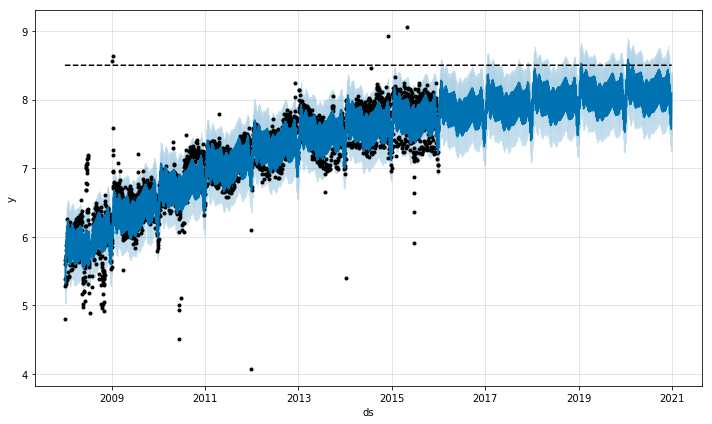
m.fit(df)

如前所述，我们可以创建一个数据框来预测未来值，不过这里要指定未来的承载能力。我们将未来的承载能力设定得和历史数据一样，并且预测未来 3 年的数据。

future = m.make_future_dataframe(periods=1826)
future['cap'] = 8.5
fcst = m.predict(future)
fig = m.plot(fcst)

预测结果如下图所示：

2.2 预测饱和减少

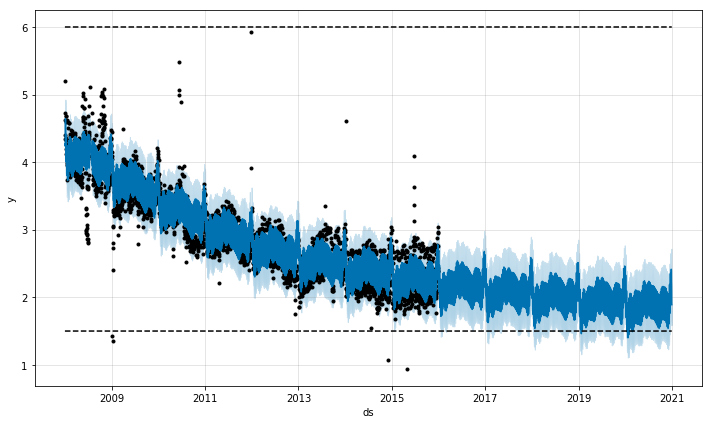
logistic增长模型还可以处理饱和最小值，方法与指定最大值的列的方式相同:

# Python
df['y'] = 10 - df['y']
df['cap'] = 6
df['floor'] = 1.5
future['cap'] = 6
future['floor'] = 1.5
m = Prophet(growth='logistic')
m.fit(df)
fcst = m.predict(future)
fig = m.plot(fcst)

结果如下图：

三、趋势突变点

在之前的部分，我们可以发现真实的时间序列数据往往在趋势中存在一些突变点。默认情况下， Prophet 将自动监测到这些点，并对趋势做适当地调整。不过，要是对趋势建模时发生了一些问题，例如：Prophet 不小心忽略了一个趋势速率的变化或者对历史数据趋势变化存在过拟合现象。如果我们希望对趋势的调整过程做更好地控制的话，那么下面将会介绍几种可以使用的方法。

3.1 Prophet 中的自动监测突变点

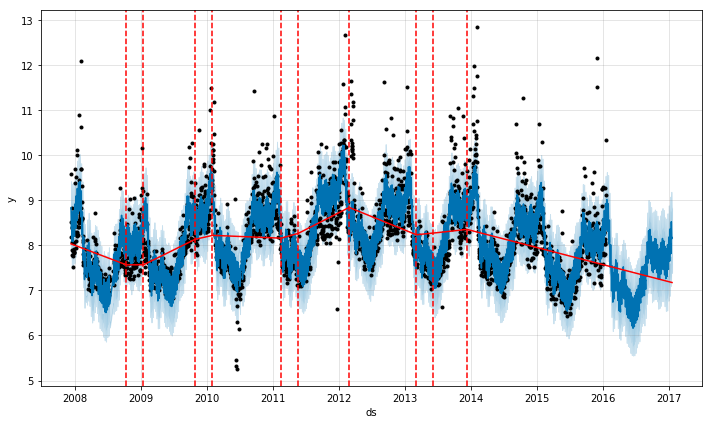
Prophet 首先是通过在大量潜在的突变点（变化速率突变）中进行识别来监测突变点的。之后对趋势变化的幅度做稀疏先验（等同于 L1 正则化）——实际上 Prophet 在建模时会存在很多变化速率突变的点，但只会尽可能少地使用它们。以第一部分中佩顿 · 曼宁的数据为例，默认下， Prophet 会识别出 25 个潜在的突变点（均匀分布在在前 80% 的时间序列数据中）。下图中的竖线指出这些潜在的突变点所在的位置。

虽然存在很多变化速率可能会突变的点，但由于做了稀疏先验，绝大多数突变点并不会包含在建模过程中。如下图所示，通过观察对每个突变点绘制的速率变化值图，可以发现这一点。

潜在突变点的数量可以通过设置 n_changepoints 参数来指定，但最好还是利用调整正则化过程来修正。

显著的突变点的位置可以通过以下代码获得：

# Python
from fbprophet.plot import add_changepoints_to_plot
fig = m.plot(forecast)
a = add_changepoints_to_plot(fig.gca(), m, forecast)

默认情况下，只有在时间序列的前80%才会推断出突变点，以便有足够的长度来预测未来的趋势，并避免在时间序列的末尾出现过度拟合的波动。这个默认值可以在很多情况下工作，但不是所有情况下都可以，可以使用changepoint_range参数进行更改。例如，Python中的m = Prophet(changepoint_range=0.9)。这意味着将在时间序列的前90%处寻找潜在的变化点。

3.2 调整趋势的灵活性

如果趋势的变化被过度拟合（即过于灵活）或者拟合不足（即灵活性不够），可以利用输入参数 changepoint_prior_scale 来调整稀疏先验的程度。默认下，这个参数被指定为 0.05 。

增加这个值，会导致趋势拟合得更加灵活。代码和图如下所示：

df = pd.read_csv('examples/example_wp_log_peyton_manning.csv')

# 拟合模型
m = Prophet(changepoint_prior_scale=0.5)
m.fit(df)

future = m.make_future_dataframe(periods=365)

forecast = m.predict(future)
fig = m.plot(forecast)

减少这个值，会导致趋势拟合得灵活性降低。代码和图如下所示：

m = Prophet(changepoint_prior_scale=0.001)
m.fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)
m.plot(forecast);

3.3 指定突变点的位置

如果你希望手动指定潜在突变点的位置而不是利用自动的突变点监测，可以使用 changepoints 参数。

代码和图如下所示：

m = Prophet(changepoints=['2014-01-01'])
m.fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)
m.plot(forecast);

四、季节性，假期效果和回归量

4.1 对假期和特征事件建模

如果需要专门对节假日或者其它的事件进行建模，你就必须得为此创建一个新的dataframe，其中包含两列（节假日 holiday 和日期戳 ds ），每行分别记录了每个出现的节假日。这个数据框必须包含所有出现的节假日，不仅是历史数据集中还是待预测的时期中的。如果这些节假日并没有在待预测的时期中被注明， Prophet 也会利用历史数据对它们建模，但预测未来时却不会使用这些模型来预测。

注：也就是说，在待预测的日期里，我们也必须指定所有出现的节假日。

你可以在这个数据框基础上再新建两列 lower_window 和 upper_window ，从而将节假日的时间扩展成一个区间 [ lower_window , upper_window ] 。举例来说，如果想将平安夜也加入到 “圣诞节” 里，就设置 lower_window = -1 , upper_window = 0 ;如果想将黑色星期五加入到 “感恩节” 里，就设置 lower_window = 0 , upper_window = 1 。

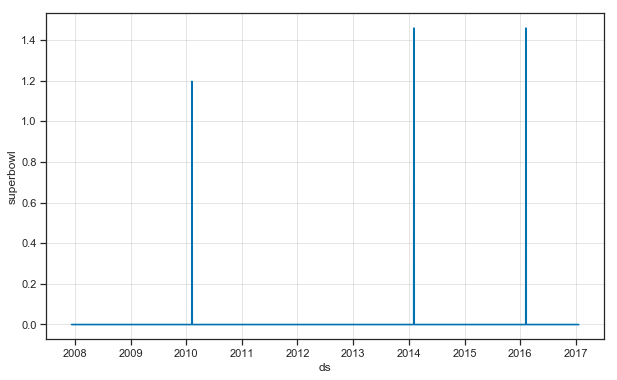
下面我们创建一个数据框，其中包含了所有佩顿 · 曼宁参加过的决赛日期：

playoffs = pd.DataFrame({
  'holiday': 'playoff',
  'ds': pd.to_datetime(['2008-01-13', '2009-01-03', '2010-01-16',
                        '2010-01-24', '2010-02-07', '2011-01-08',
                        '2013-01-12', '2014-01-12', '2014-01-19',
                        '2014-02-02', '2015-01-11', '2016-01-17',
                        '2016-01-24', '2016-02-07']),
  'lower_window': 0,
  'upper_window': 1,
})
superbowls = pd.DataFrame({
  'holiday': 'superbowl',
  'ds': pd.to_datetime(['2010-02-07', '2014-02-02', '2016-02-07']),
  'lower_window': 0,
  'upper_window': 1,
})
holidays = pd.concat((playoffs, superbowls))

上述代码中，我们将超级碗的日期既记录在了决赛的日期数据框中，也记录在了超级碗的日期数据框中。这就会造成超级碗日期的效应会在决赛日期的作用下叠加两次。

一旦这个数据框创建好了，就可以通过传入 holidays 参数使得在预测时考虑上节假日效应。这里我们仍以第一部分中佩顿 · 曼宁的数据为例：

df = pd.read_csv('examples/example_wp_log_peyton_manning.csv')

m = Prophet(holidays=holidays)
m.fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)

可通过 forecast 数据框，来展示节假日效应：

# 看一下假期的最后10行数据
forecast[(forecast['playoff'] + forecast['superbowl']).abs() > 0][
        ['ds', 'playoff', 'superbowl']][-10:]

在成分分析的图中，如下所示，也可以看到节假日效应。我们可以发现，在决赛日期附近有一个穿透，而在超级碗日期时穿透则更为明显。

fig = m.plot_components(forecast)

可以使用 plot_forecast_component（从fbprophet.plot导入）来画出独立的节假日的成分。类似如下代码：

from fbprophet.plot import plot_forecast_component
m.plot_forecast_component(forecast, 'superbowl')

4.2 季节性的傅里叶级数

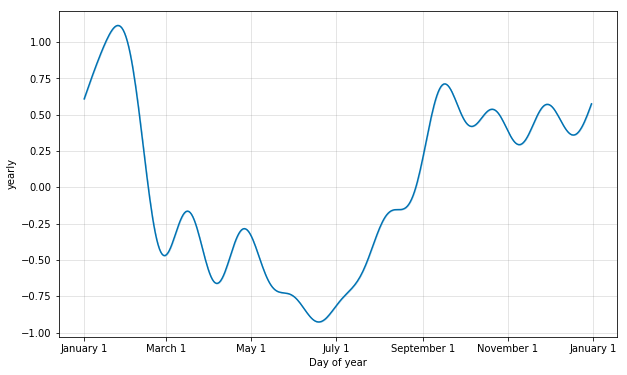
季节性是用部分傅里叶和估计的。有关完整的细节，请参阅论文，以及维基百科上的这个图，以说明部分傅里叶和如何近似于一个线性周期信号。部分和(order)中的项数是一个参数，它决定了季节性的变化有多快。为了说明这一点，我们仍似乎用第一部分中佩顿 · 曼宁的数据。每年季节性的默认傅立叶级数是10，这就产生了这样的拟合:

# Python
from fbprophet.plot import plot_yearly
m = Prophet().fit(df)
a = plot_yearly(m)

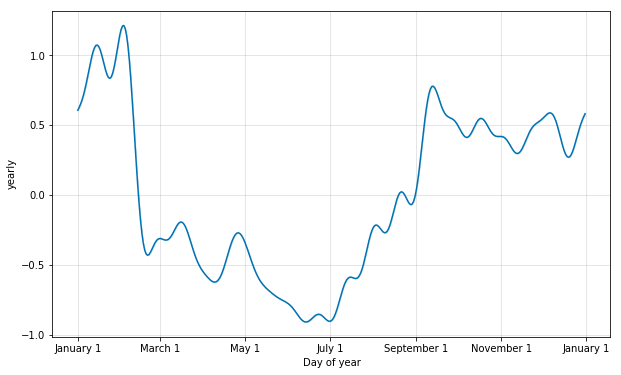
默认值10通常是合适的，但是当季节性需要适应更高频率的变化时，它们可以增加，并且通常不那么平滑。在实例化模型时，可以为每个内置季节性指定傅立叶级数，这里增加到20:

from fbprophet.plot import plot_yearly
m = Prophet(yearly_seasonality=20).fit(df)
a = plot_yearly(m)

可以看到，曲线更加的多变了。增加傅立叶项的数量可以使季节性适应更快的变化周期，但也可能导致过度拟合:N个傅立叶项对应于用于建模周期的2N个变量。

4.3 自定义季节性因素

如果时间序列超过两个周期，Prophet将默认适合每周和每年的季节性。对于子日（sub-daily ）时间序列，它也将适合每日的季节性。在Python中，可以使用add_seasality方法添加其它季节性(如每月、每季、每小时)。

这个函数的输入是一个名字，季节性的周期，以及季节性的傅里叶order。作为参考，默认情况下，Prophet为周季节性设定的傅立叶order为3，为年季节性设定的为10。add_seasality的一个可选输入是该季节性组件的先验规模。

作为一个例子，我们仍使用佩顿 · 曼宁的数据，但是用每月的季节性替换每周的季节性。每月的季节性将出现在组件图中:

m = Prophet(weekly_seasonality=False)
m.add_seasonality(name='monthly', period=30.5, fourier_order=5)
forecast = m.fit(df).predict(future)
fig = m.plot_components(forecast)

4.4 对节假日和季节性设定先验规模

如果发现节假日效应被过度拟合了，通过设置参数 holidays_prior_scale 可以调整它们的先验规模来使之平滑，默认下该值取 10 。

减少这个参数会降低假期效果:

m = Prophet(holidays=holidays, holidays_prior_scale=0.05).fit(df)
forecast = m.predict(future)
forecast[(forecast['playoff'] + forecast['superbowl']).abs() > 0][
    ['ds', 'playoff', 'superbowl']][-10:]

代码输出结果如下所示：

和之前相比，节假日效应的规模被减弱了，特别是对观测值较少的超级碗而言。类似的，还有一个 seasonality_prior_scale 参数可以用来调整模型对于季节性的拟合程度。

可以通过在节假日的dataframe中包含一个列prior_scale来单独设置先验规模。独立的季节性的先验规模可以作为add_seasonality的参数传递。例如，可以使用以下方法设置每周季节性的先验规模:

m = Prophet()
m.add_seasonality(
    name='weekly', period=7, fourier_order=3, prior_scale=0.1)

4.5 附加的回归量

可以使用add_regressor方法将附加的回归量添加到模型的线性部分。包含回归值的列需要同时出现在拟合数据格式（fit）和预测数据格式(predict)中。例如，我们可以在NFL赛季的周日添加附加的效果。在成分图上，这种效果会出现在“extra_regre_”图中:

# 判断是否是NFL赛季的周日
def nfl_sunday(ds):
    date = pd.to_datetime(ds)
    if date.weekday() == 6 and (date.month > 8 or date.month < 2):
        return 1
    else:
        return 0
df['nfl_sunday'] = df['ds'].apply(nfl_sunday)

m = Prophet()
m.add_regressor('nfl_sunday')
m.fit(df)

future['nfl_sunday'] = future['ds'].apply(nfl_sunday)

forecast = m.predict(future)
fig = m.plot_components(forecast)

NFL周日也可以使用之前描述的“节假日”的接口，通过创建一个过去和未来NFL周日的list。add_regressor函数为定义附加的线性回归函数提供了一个更通用的接口，特别是它不要求回归函数是二进制指示器。

add_regressor函数具有可选的参数，用于指定先验规模(默认情况下使用节假日先验规模)，和指定是否标准化回归量。help(Prophet.add_regressor)可以查看相关参数。

附加的回归量必须要知道历史和未来的日期。因此，它要么是已知未来值(比如nfl_sunday)，要么是其他地方已经单独预测出的结果。如果回归量在整个历史中都是不变的，则Prophet会引发一个错误，因为没有任何东西可以fit它。

附加的回归量被放在模型的线性分量中，所以依赖于附加的回归量时间序列作为底层模型的加法或乘法因子。

五、乘法季节性

默认情况下，Prophet能够满足附加的季节性，这意味着季节性的影响是加到趋势中得到了最后的预报（yhat）。航空旅客数量的时间序列是一个附加的季节性不起作用的例子：

df = pd.read_csv('../examples/example_air_passengers.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(50, freq='MS')
forecast = m.predict(future)
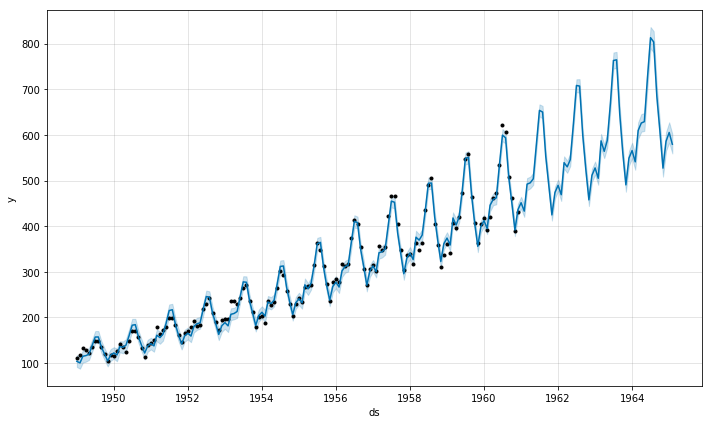
fig = m.plot(forecast)

这个时间序列有一个明显的年度周期，但预测中的季节性在时间序列开始时太大，在结束时又太小。在这个时间序列中，季节性并不是Prophet所假定的是一个恒定的加性因子，而是随着趋势在增长。这就是乘法季节性（multiplicative seasonality）。

Prophet可以通过设置seasonality_mode='multiplicative'来建模乘法季节性:

m = Prophet(seasonality_mode='multiplicative')
m.fit(df)
forecast = m.predict(future)
fig = m.plot(forecast)

看一下乘法的成分图：

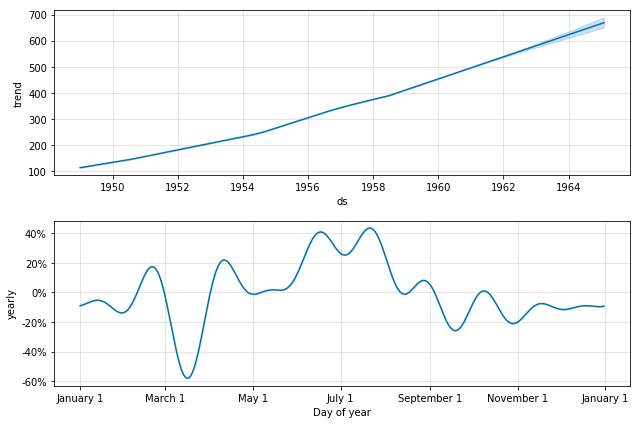
fig = m.plot_components(forecast)

与第一部分对成分图分析类似，我们这里对乘法模型的成分图进行一个分析：

①图1是根据trend画出来的，图2是根据yearly画出来的。

②因为是乘法模型，有：forecast[‘multiplicative_terms’] = forecast[‘yearly’]；因此：forecast[‘yhat’] = forecast[‘trend’] * (1+forecast[‘multiplicative_terms’])。

使用seasonality_mode='multiplicative'，节假日也将被建模为乘法效果。

③因为是乘法模型，’additive_terms’, ‘additive_terms_lower’, ‘additive_terms_upper’这3列为0。

默认情况下，任何添加的季节性或额外的回归量都可以使用seasality_mode设置为加法或者是乘法。但假如在添加季节性或回归量时，可以通过指定mode=’ addiative ‘或mode=’ ative’作为参数来覆盖之前的设定。

例如，这个模块将内置的季节性设置为乘法，但使用一个附加的季度季节性来覆盖原本的乘法，这时候季度季节性就是加法了。

# Python
m = Prophet(seasonality_mode='multiplicative')
m.add_seasonality('quarterly', period=91.25, fourier_order=8, mode='additive')

额外的加法的季度季节性将出现在成分图的单独的面板上。

这个时候是时间序列的混合模型：forecast[‘yhat’] = forecast[‘trend’] * (1+forecast[‘multiplicative_terms’]) + forecast[‘additive_terms’]。

六、预测区间

默认情况下， Prophet 的返回结果中会包括预测值 yhat 的预测区间。当然，预测区间的估计需建立在一些重要的假设前提下。

在预测时，不确定性主要来源于三个部分：趋势中的不确定性、季节效应估计中的不确定性和观测值的噪声影响。

6.1 趋势的不确定性

预测中，不确定性最大的来源就在于未来趋势改变的不确定性。在之前的时间序列实例中，我们可以发现历史数据具有明显的趋势性。 Prophet 能够监测并去拟合它，但是我们期望得到的趋势改变究竟会如何走向呢？或许这是无解的，因此我们尽可能地做出最合理的推断，假定 “未来将会和历史具有相似的趋势” 。尤其重要的是，我们假定未来趋势的平均变动频率和幅度和我们观测到的历史值是一样的，从而预测趋势的变化并通过计算，最终得到预测区间。

这种衡量不确定性的方法具有以下性质：变化速率灵活性更大时（通过增大参数 changepoint_prior_scale 的值），预测的不确定性也会随之增大。原因在于如果将历史数据中更多的变化速率加入了模型，也就代表我们认为未来也会变化得更多，就会使得预测区间成为反映过拟合的标志。

预测区间的宽度（默认下，是 80% ）可以通过设置 interval_width 参数来控制：

m = Prophet(interval_width=0.95).fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)

由于预测区间估计时假定未来将会和过去保持一样的变化频率和幅度，而这个假定可能并不正确，所以预测区间的估计不可能完全准确。

6.2 季节的不确定性

默认情况下， Prophet 只会返回趋势中的不确定性和观测值噪声的影响。你必须使用贝叶斯取样的方法来得到季节效应的不确定性，可通过设置 mcmc.samples 参数（默认下取 0 ）来实现。下面使用佩顿 · 曼宁的数据为例：

m = Prophet(mcmc_samples=500).fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)
# 报错：UnboundLocalError: local variable 'pool' referenced before assignment

上述代码将最大后验估计（ MAP ）取代为马尔科夫蒙特卡洛取样（ MCMC ），并且将计算时间从 10 秒延长到 10 分钟。

如果做了全取样，就能通过绘图看到季节效应的不确定性了：

m.plot_components(forecast);

可以使用m.predictive_samples(future)方法在Python中访问原始的后验预测样本。

在PyStan有一些针对Windows的上游问题，这使得MCMC采样非常缓慢。在Windows中，MCMC采样的最佳选择是在Linux VM中使用R或Python。

因此，我的上述代码会出错，季节的不确定性在我windows的python中跑不动，暂时忽略，了解即可。

七、异常值

异常值主要通过两种方式影响 Prophet 预测结果。下面我们使用之前使用过的 R 语言维基百科主页对数访问量的数据来建模预测，只不过使用存在时间间隔并不完整的数据：


df = pd.read_csv('examples/example_wp_log_R_outliers1.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(periods=1096)
forecast = m.predict(future)
m.plot(forecast);

如上输出图所示，趋势预测看似合理，预测区间的估计却过于广泛。 Prophet 虽能够处理历史数据中的异常值，但仅仅是将它们与趋势的变化拟合在一起，认为未来也会有类似的趋势变化。

处理异常值最好的方法是移除它们，而 Prophet 是能够处理缺失数据的。如果在历史数据中某行的值为空（ NA ），但是在待预测日期数据框 future 中仍保留这个日期，那么 Prophet 依旧可以给出该行的预测值。

# 将2010年一年的数据设为缺失
df.loc[(df['ds'] > '2010-01-01') & (df['ds'] < '2011-01-01'), 'y'] = None
model = Prophet().fit(df)
model.plot(model.predict(future));

上述这个实例虽然影响了不确定性的估计，却没有影响到主要的预测值 yhat 。但是，现实往往并非如此，接下来，在上述数据集基础上加入新的异常值后再建模预测：

df = pd.read_csv('examples/example_wp_log_R_outliers2.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(periods=1096)
forecast = m.predict(future)
m.plot(forecast);

这里 2015年 6 月存在一些异常值破坏了季节效应的估计，因此未来的预测也会永久地受到这个影响。最好的解决方法就是移除这些异常值：

# 将2015年前半年的数据设为缺失
df.loc[(df['ds'] > '2015-06-01') & (df['ds'] < '2015-06-30'), 'y'] = None
m = Prophet().fit(df)
m.plot(m.predict(future));

八、非日数据

8.1 子日数据

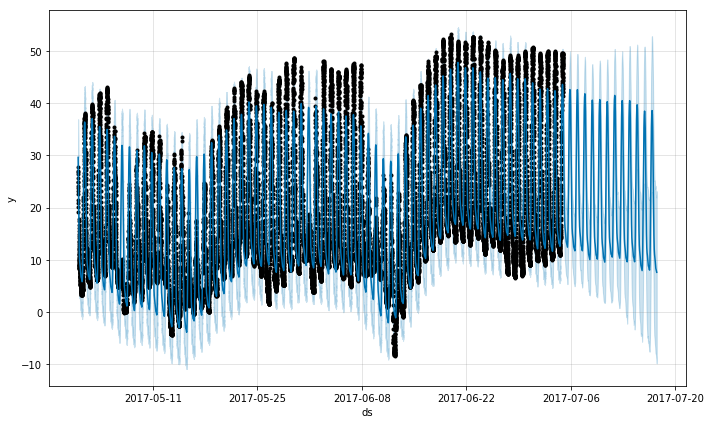
Prophet可以通过在ds列中传递一个带有时间戳的dataframe来对时间序列进行子日（Sub-daily）观测。时间戳的格式应该是YYYY-MM-DD – HH:MM:SS。当使用子日数据时，日季节性将自动匹配。在这里，我们用5分钟的分辨率数据集(约塞米蒂的每日温度)对Prophet进行数据匹配:

df = pd.read_csv('examples/example_yosemite_temps.csv')
m = Prophet(changepoint_prior_scale=0.01).fit(df)
future = m.make_future_dataframe(periods=300, freq='H')
fcst = m.predict(future)
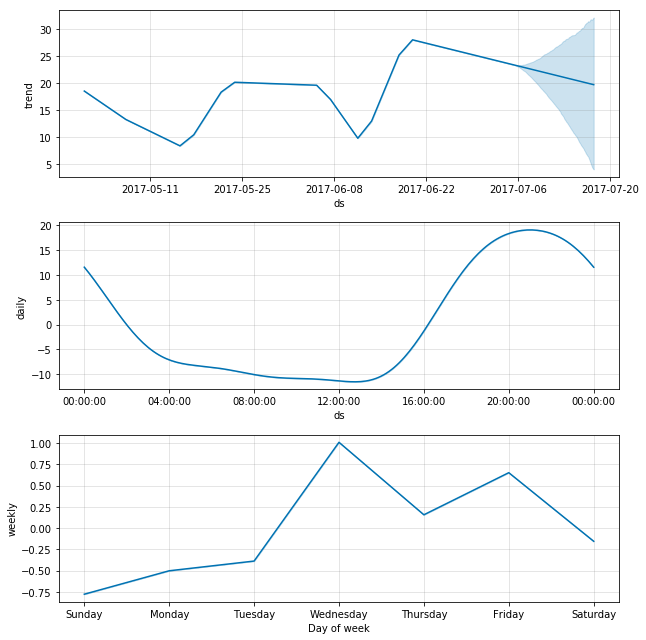
fig = m.plot(fcst)

成分图中的日季节性:

fig = m.plot_components(fcst)

8.2 有规则间隔的数据

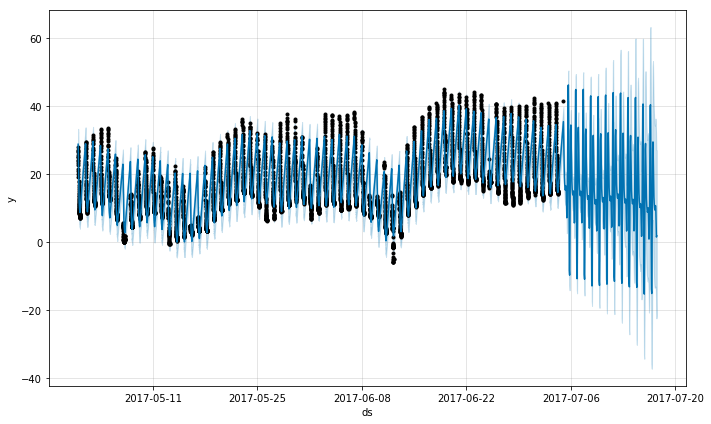
假设上面的数据集只有每天早上6点之前的观测值:

df2 = df.copy()
df2['ds'] = pd.to_datetime(df2['ds'])
# 只保留每天早上6点之前的数据
df2 = df2[df2['ds'].dt.hour < 6]
m = Prophet().fit(df2)
future = m.make_future_dataframe(periods=300, freq='H')
fcst = m.predict(future)
fig = m.plot(fcst)

这个预测看起来很差，未来的波动比历史上看到的要大得多。这里的问题是，我们将每天的循环安排在一个时间序列中，这个时间序列中只有一天的一部分数据(12a到6a)。因此，每天的季节性在一天剩下的时间里是不受约束的，估计也不准确。解决方案是只对有历史数据的时间窗进行预测。这里，这意味着限制未来dataframe的时间（从12a到6a）:

future2 = future.copy()
future2 = future2[future2['ds'].dt.hour < 6]
fcst = m.predict(future2)
fig = m.plot(fcst)

同样的原理也适用于数据中有规则间隔的其他数据集。例如，如果历史只包含工作日，那么应该只对工作日进行预测，因为不会很好地估计每周的季节性。

8.3 月数据

可以使用Prophet来匹配每月的数据。然而，Prophet 的基本模型是连续时间的，这意味着如果将模型与每月的数据相匹配，然后要求每天的预测，我们会得到奇怪的结果。

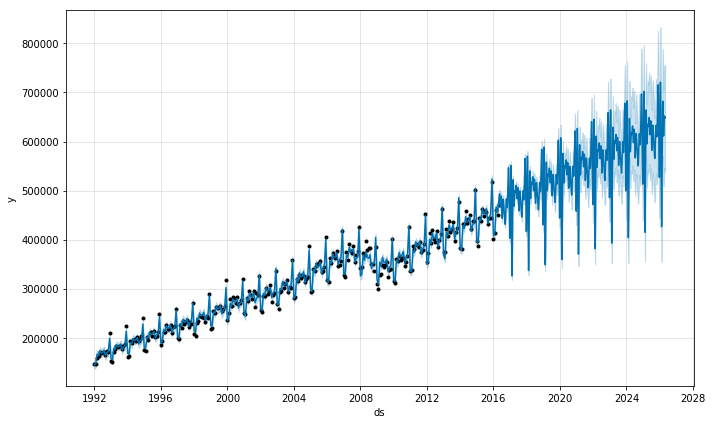
下面使用美国零售业销售量数据来预测未来 10 年的情况：

df = pd.read_csv('examples/example_retail_sales.csv')
m = Prophet().fit(df)
future = m.make_future_dataframe(periods=3652)
fcst = m.predict(future)
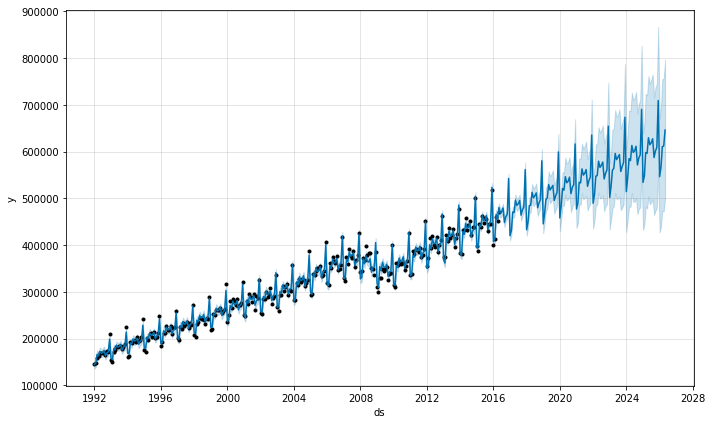
m.plot(fcst);

预测结果看起来非常杂乱，原因正是在于这个特殊的数据集使用的是月数据。当我们拟合年度效应时，只有每个月第一天的数据，而且对于其他天的周期效应是不可测且过拟合的。当你使用 Prophet 拟合月度数据时，可以通过在 make_future_dataframe 中传入频率参数只做月度的预测。

future = m.make_future_dataframe(periods=120, freq='M')
fcst = m.predict(future)
m.plot(fcst);

九、诊断

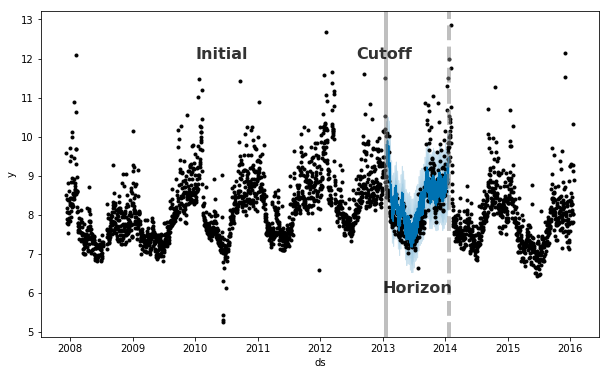
Prophet包含时间序列交叉验证功能，以测量使用历史数据的预测误差。这是通过在历史记录中选择截止点来完成的，对于每一个都只使用该截止点之前的数据来拟合模型。然后，我们可以将预测值与实际值进行比较。这张图展示了对Peyton Manning数据集的模拟历史预测，该模型适用于5年的初始历史，并在1年的时间范围内进行了预测。

源论文中进一步描述了模拟的历史预测。

这个交叉验证过程可以使用cross_validation函数自动完成一系列历史截断。我们指定预测水平(horizon)，然后选择初始训练期(initial)的大小和截断之间的间隔(period)。默认情况下，初始训练期设置为horizon的三倍，每半个horizon就有一个截断。

注：这里需要解释下horizon，initial和period的意义：initial代表了一开始的时间是多少，period代表每隔多长时间设置一个cutoff，horizon代表每次从cutoff往后预测多少天。

cross_validation的输出是一个dataframe，在每个模拟预测日期和每个截断日期都有真实值y和样本预测值yhat。特别地，对在cutoff 和cutoff + horizon之间的每一个观测点都进行了预测。然后，这个dataframe可以用来度量yhat和y的错误。

在这里，我们做交叉验证来评估预测horizon在365天的性能，从第一次截止时730天的训练数据开始，然后每180天进行一次预测。在这个8年的时间序列中，这相当于11个总预测。

注：Peyton Manning数据一共大约8年多（2007/12/10 – 2016/01/20）的数据。

根据上面对horizon，initial和period的解释：容易得到为什么是11个总预测。因为最后一个也要预测365天，所有最后一个cutoff在2015-01-20，从2007-12-19数730天是2010-02-15，则在2010-02-15到2015-01-20共有1800天，对应着10个cutoff，最后1个cutoff在2015-01-20，因此共11个cutoff。

from fbprophet.diagnostics import cross_validation
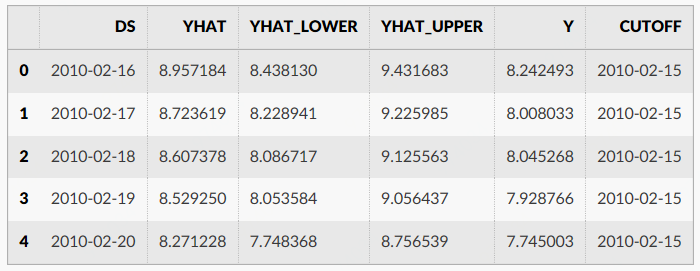
df_cv = cross_validation(m, initial='730 days', period='180 days', horizon = '365 days')
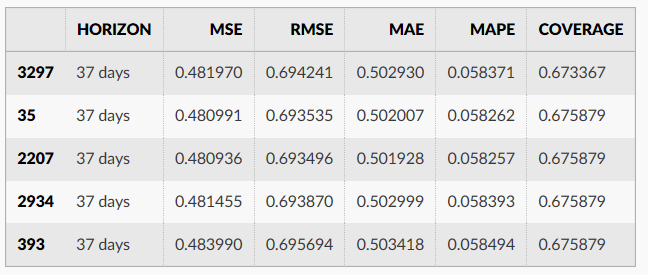
df_cv.head()

performance_metrics作为离截止点(预测的未来距离)的函数，可用于计算关于预测性能的一些有用统计数据(如与y相比时yhat、yhat_lower和yhat_upper)。计算得到的统计信息包括均方误差(mean squared error, MSE)、均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对误差(mean absolute percent error, MAPE)以及yhat_lower和yhat_upper估计的覆盖率。这些都是在df_cv中通过horizon (ds – cutoff)排序后预测的滚动窗口中计算出来的。默认情况下，每个窗口都会包含10%的预测，但是可以通过rolling_window参数来更改。

from fbprophet.diagnostics import performance_metrics
df_p = performance_metrics(df_cv)
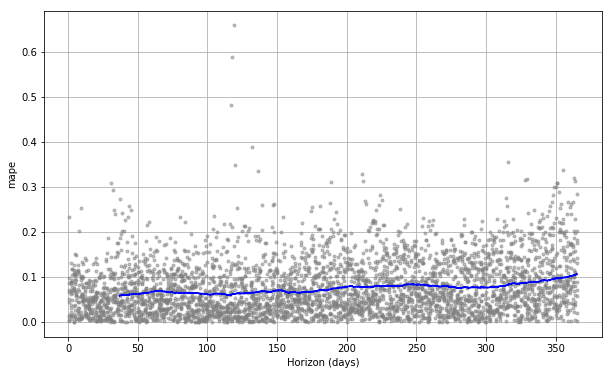
df_p.head()

交叉验证性能指标可以用plot_cross_validation_metric可视化，这里显示的是MAPE。点表示df_cv中每个预测的绝对误差百分比。蓝线显示的是MAPE，均值被取到滚动窗口的圆点。我们可以看到，对于一个月后的预测，误差在5%左右，而对于一年之后的预测，误差会增加到11%左右。

# Python
from fbprophet.plot import plot_cross_validation_metric
fig = plot_cross_validation_metric(df_cv, metric='mape')

图中滚动窗口的大小可以通过可选参数rolling_window更改，该参数指定在每个滚动窗口中使用的预测比例。默认值为0.1，即每个窗口中包含的df_cv的10%行;增大值得话将导致图中平均曲线更平滑。

初始周期应该足够长，以捕获模型的所有特性，特别是季节性和额外的回归变量:对年的季节性至少保证一年，对周的季节性至少保证一周，等等。

十、与机器学习算法的对比

与先进的机器学习算法如LGBM相比，Prophet作为一个时间序列的工具，优点就是不需要特征工程就可以得到趋势，季节因素和节假日因素，但是这同时也是它的缺点之一，它无法利用更多的信息，如在预测商品的销量时，无法利用商品的信息，门店的信息，促销的信息等。

因此，寻找一种融合的方法是一个迫切的需求。

今天的文章时间序列模型_建立时间序列模型的步骤分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：http://bianchenghao.cn/76334.html

时间序列 模型_建立时间序列模型的步骤

一、简易入门