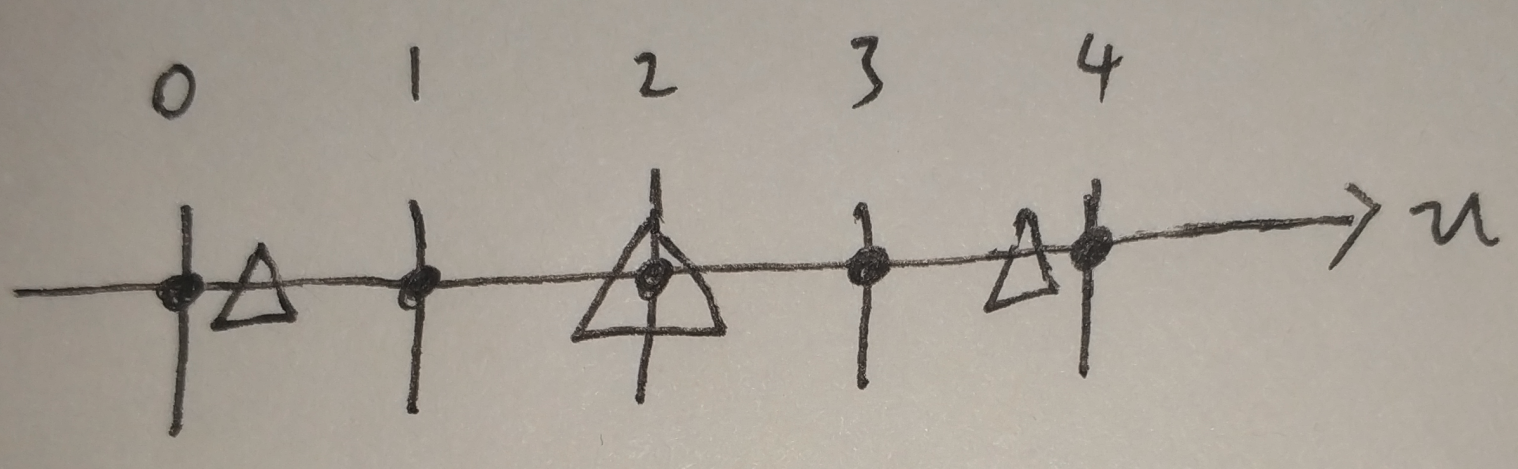二维线性插值计算公式_数字图像处理双线性插值例题

声明

本文整合了网上内容，引用出处见文末参考链接，如有侵权请联系我删除。

双线性插值(Bilinear Interpolation)性质

• 当对相邻四个像素点采用双线性插值时，所得表面在邻域处是吻合的，但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节产生退化，这种现象在进行图像放大时尤其明显。

单线性插值原理

注：单线性插值是我自己取的名字，为了便于说明

为了方便说明，先以一条直线的插值为例，说明直线一维的线性插值，再说明二维的。

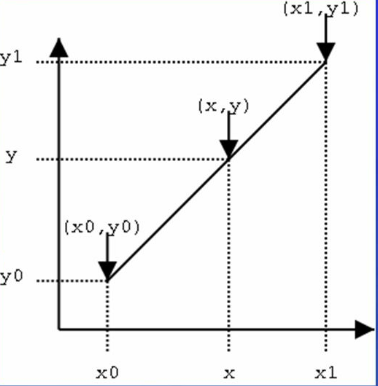
如图，我们已经知道在x=x0处和x=x1处的y值分别为y0和y1，现在要插值得到x=x处的y值是多少。线性插值的原理就是在已知的两点之间作一条线段，用来估计两点之间的任一未知点的y值。

根据线段(x0,y0)->(x,y)的斜率与线段(x0,y0)->(x1,y1)相等，有
$$\frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0}$$
所以
$$y=\frac{y_1-y_0}{x_1-x_0}\times (x-x_0)+y_0$$

双线性插值原理

基本原理

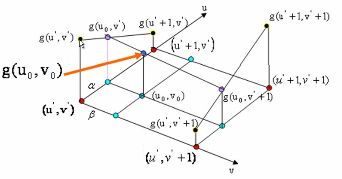
有了上面单线性插值的介绍，现在来说明双线性插值原理。如下图所示，我们已知4个点(u’, v’)、(u’+1, v’)、(u’+1, v’+1)、(u’, v’+1)的灰度值分别为g(u’, v’)、g(u’+1, v’)、g(u’+1, v’+1)、g(u’, v’+1)。现在要通过这4个点插值得到点(u0, v0)的灰度值g(u0, v0)。

我们可以将插值分解为多个单线性插值来处理：

1. 在v=v’这条直线的u方向上，通过单线性插值得到点(u0, v’)的灰度值 ：
   $$g(u_0,v^{\prime })=\frac{g(u^{\prime }+1,v^{\prime })-g(u^{\prime },v^{\prime })}{u^{\prime }+1-u^{\prime }}\times (u_0-u^{\prime })+g(u^{\prime },v^{\prime })$$

2. 在v=v’+1这条直线的u方向上，通过单线性插值得到点(u0, v’+1)的灰度值：
   $$g(u_0,v^{\prime }+1)=\frac{g(u^{\prime }+1,v^{\prime }+1)-g(u^{\prime },v^{\prime }+1)}{u^{\prime }+1-u^{\prime }}\times (u_0-u^{\prime })+g(u^{\prime },v^{\prime }+1)$$

3. 在u=u0这条直线的v方向上，通过单线性插值得到点(u0, v0)的灰度值：
   $$g(u_0,v_0)=\frac{g(u_0,v^{\prime }+1)-g(u_0,v^{\prime })}{v^{\prime }+1-v^{\prime }}\times (v_0-v^{\prime })+g(u_0,v^{\prime })$$

简化公式

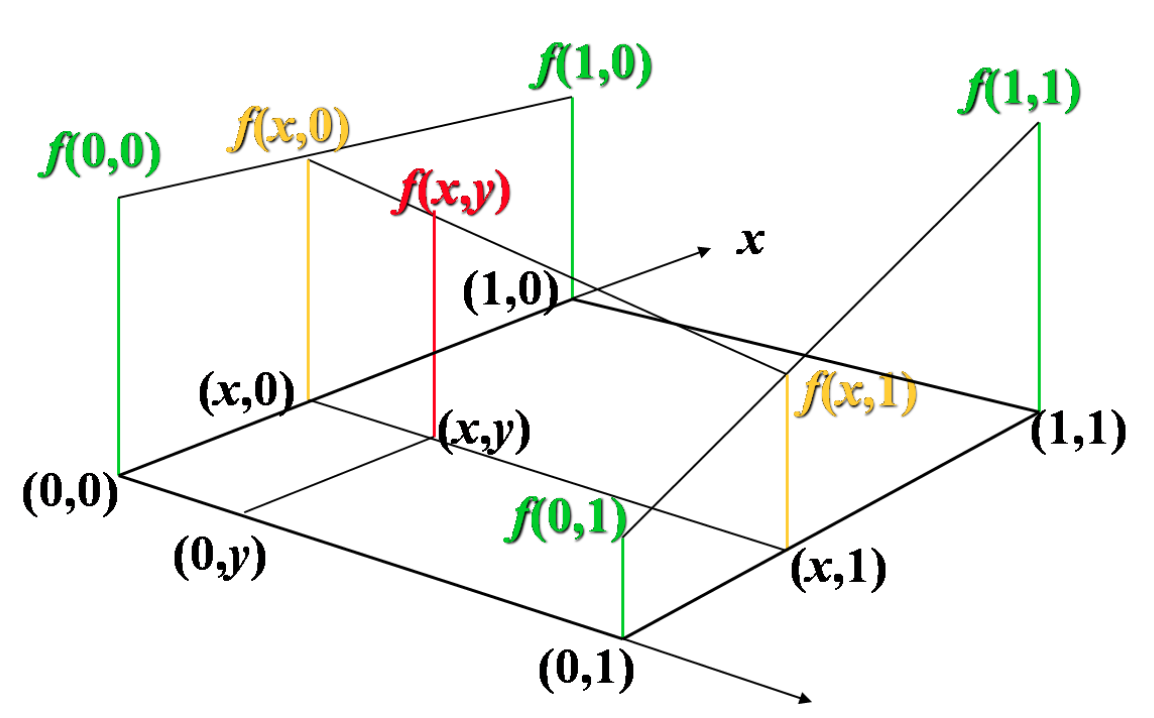
上面的公式比较复杂，如果选择一个坐标系统，如下图，使得的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以简化为：
$$g(u_0,v_0)=g(0,0)(1-u_0)(1-v_0)+g(1,0)u_0(1-v_0)+g(0,1)(1-u_0)v_0+g(1,1)u_0{v}_0$$
或者用矩阵运算表示为：
$$g(u_0,v_0)=\left[\begin{array}{cc}1-u_0& u_0\end{array}\right]\left[\begin{array}{cc}g(0,0)& g(0,1)\\ g(1,0)& g(1,1)\end{array}\right]\left[\begin{array}{c}1-v_0\\ v_0\end{array}\right]$$

图像坐标的前向映射和反向映射

参考：图像变换——向前映射和向后映射

前向映射

• 计算量大。计算量与原图大小有关，随着原图大小增大而增大。
• 不方便并行。输出图像某一点的像素值不能直接得到，需要遍历输入图像的所有像素值，对其进行坐标变换，分配像素值到整数位置，才能得到输出图像各像素点的像素值。
• 必须归一化，虽然分配系数之和 $(1-u_0)(1-v_0)+u_0(1-v_0)+(1-u_0)v_0+u_0{v}_0$ 为1。但输出图像上每个点的像素值是多个分配值叠加而成的，不能保证所有分配到其上的权重之和为1。因此必须记录下所有分配到其上的权重并累加起来，最后利用累加权重进行归一化，才能得到正确的插值结果。
• 可能出现空洞？如果输出图像比原图像大很多的话，可能会有空洞？例如原图两个相邻像素映射到输出图像中相距几十个像素距离，那他们中间的像素值时不是不好插值了？

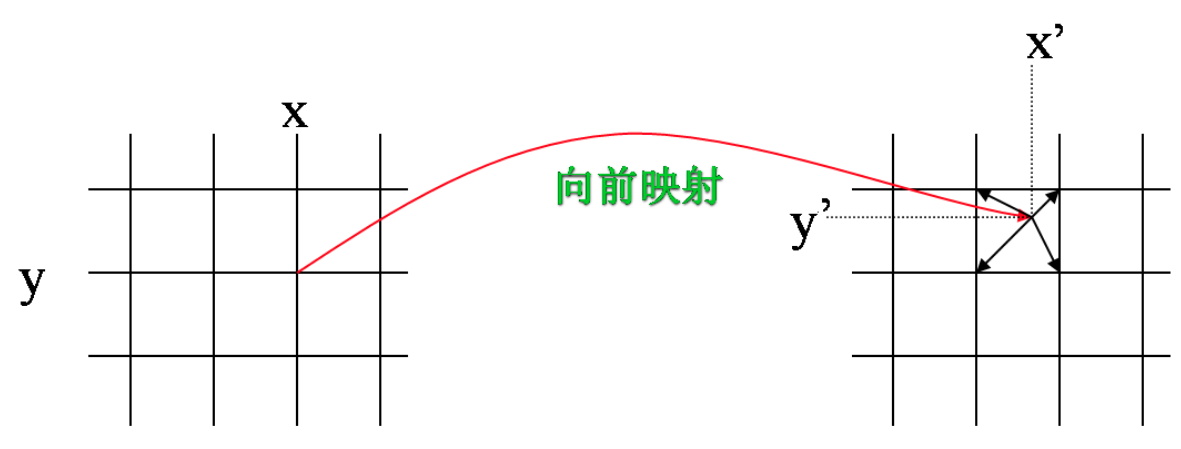
下图为向前映射的示意图。输入图像上整数点坐标映射到输出图像之后，变成了非整数点坐标。因此，需要将其像素值按一定权重分配到其周围四个像素点上。对于输出图像而言，其整数点像素值周围会有很多输入图像像素映射过来，每个到其周围的非整数点像素值都会分配一定的灰度值到它上面，将这些分配而来的像素值叠加，就是输出图像整数点位置的像素值。由于这个分配、叠加的特性，向前映射法有时也叫像素移交映射。

因此，对于向前映射而言，输出图像某一点的像素值不能直接得到，需要遍历输入图像的所有像素值，对其进行坐标变换，分配像素值到整数位置，才能得到输出图像各像素点的像素值。这是向前映射法的缺点。

对向前映射而言，虽然分配系数之和 $(1-u_0)(1-v_0)+u_0(1-v_0)+(1-u_0)v_0+u_0{v}_0$ 为1。但输出图像上每个点的像素值是多个分配值叠加而成的，不能保证所有分配到其上的权重之和为1。因此必须记录下所有分配到其上的权重并累加起来，最后利用累加权重进行归一化，才能得到正确的插值结果。

反向映射

• 计算量小。计算量与输出图像大小有关，随着输出图像大小增大而增大。
• 方便并行。将输出图像某个像素点映射回原图，取原图相邻四个点插值可直接得到，不用遍历完整个原图。
• 不需要归一化。以双线性插值为例，对反向映射而言，系数之和 $(1-u_0)(1-v_0)+u_0(1-v_0)+(1-u_0)v_0+u_0{v}_0$ 为1。
• 不会出现空洞。

通常我们都使用反向映射。

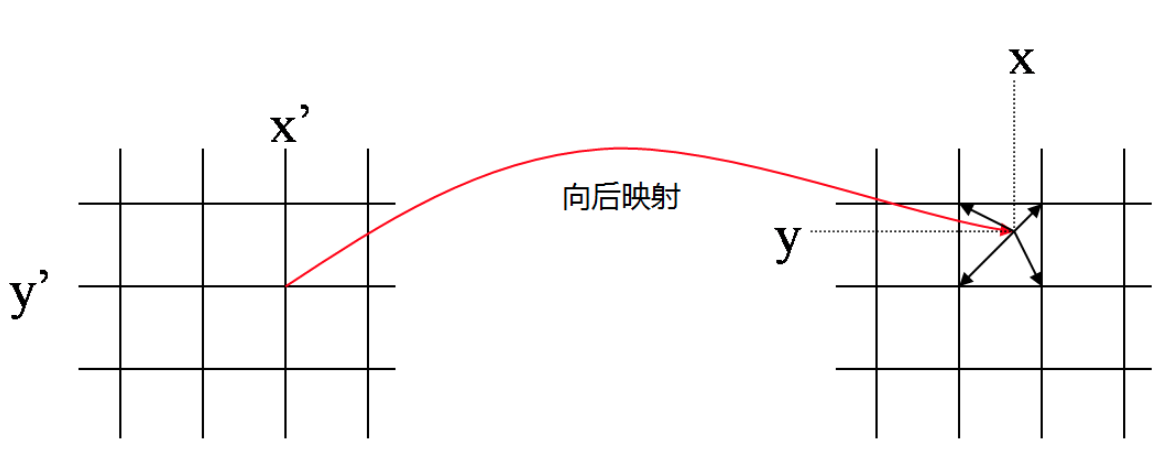
向后映射法就比较直观。在这种情况下，我们知道输出图像上整数点位置(x’,y’)在变换前位于输入图像上的位置(x,y)，一般来说这是个非整数点位置，利用其周围整数点位置的输入图像像素值进行插值，就得到了该点的像素值。我们遍历输出图像，经过坐标变换、插值两步操作，我们就能将其像素值一个个地计算出来，因此向后映射又叫图像填充映射。如下图所示。

以双线性插值为例，对反向映射而言，系数之和 $(1-u_0)(1-v_0)+u_0(1-v_0)+(1-u_0)v_0+u_0{v}_0$ 为1。

原图像和输出图像几何中心的对齐

参考：双线性插值算法及需要注意事项

如果按照上面的方法进行双线性插值，你会发现计算出来的结果和matlab、openCV对应的resize（）函数得到的结果不一样。那这个究竟是怎么回事呢？

其实答案很简单，就是坐标系的选择问题，或者说源图像和目标图像之间的对应问题。

以图像缩小为例说明问题。假设源图像大小为w1xh1，目标图像为w2xh2。那么两幅图像的边长比分别为：w1/w2和h1/h2。目标图像的像素点(j, i)（第i行j列）可以通过边长比对应回源图像。其对应坐标为（ $j\ast w1/w2,i\ast w1/w2$ ）。

float u = j*w1/w2; float v = i*w1/w2; 

注意：我们的坐标是从0开始的，即640×480大小的图像，它的宽和高取值范围分别是[0, 639]和[0,479]。这个坐标对齐于左上角，但不是几何中心对齐的，会有问题，每进行一个未对齐的处理，都会使得图像往左上角偏移一点点，下面会进行说明。

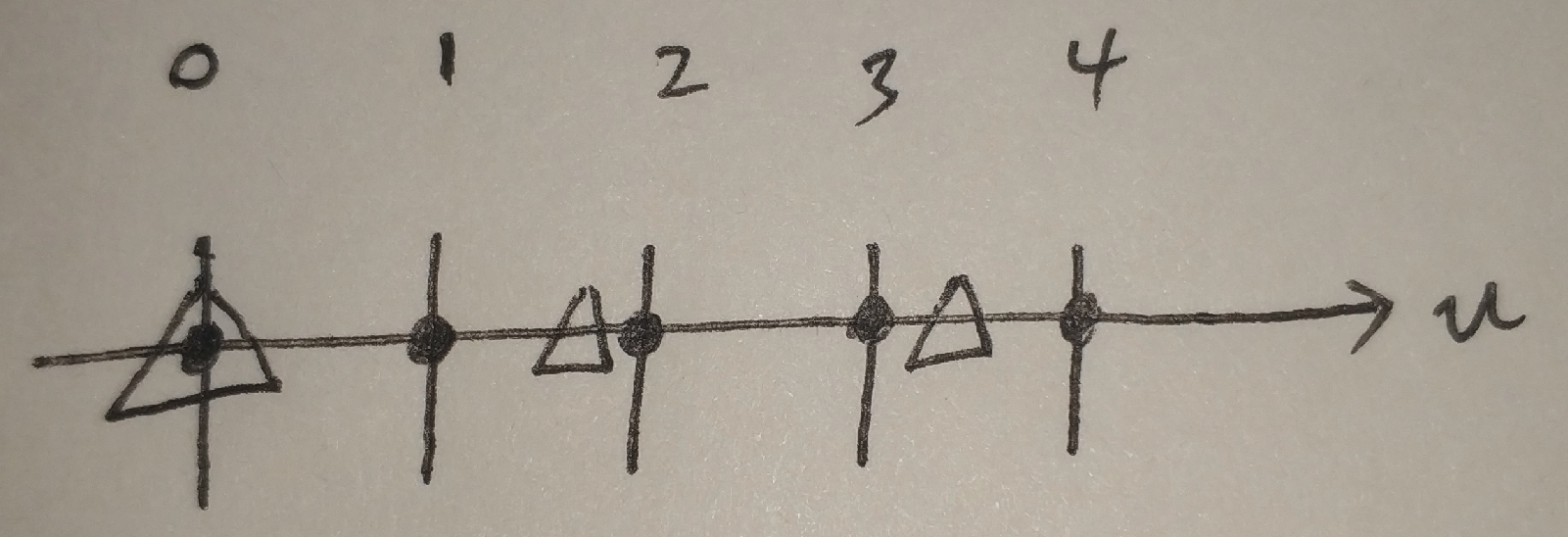
这样的计算会使得像素映射回原图偏左上角。例如当原图像大小为5×5，目标图像为3×3时，映射关系如下，为了方便，这里只画出了图像的第一行：

上图中，黑点表示原图第一行的5个像素，三角形表示目标图第一行的3个像素映射回原图所在的位置。有没有发现有一点奇怪？目标图像的像素值是在原图中靠左位置取的。而实际上，我们都知道，正确的方式应该如下图：

后面这幅图是把图像几何中心对齐了的，那么如何才能得到这种正确的映射关系呢？我们可以看一看，为什么原来的坐标映射关系会出错。

因为图像坐标从0开始，要想几何中心对齐，意味着3×3图像中间元素(u=1)要和5×5图像中间元素(u=2)重合，但是按照前面的计算公式，$u=j\ast w1/w2;$ 可以得到

3×3图像中间元素(u=1)在5×5图像中的坐标为1.666，没有和u=2对齐。这一切的错误的源头正是因为图像坐标从0开始！这导致了图像右边界坐标永远比宽要少1，即宽640图像的坐标最大只有639。

要解决这个问题，我们只需要将图像坐标从0.5开始即可。这样处理后，对于640宽的图像，图像左边界为0.5，与0相差0.5；图像右边界为639.5，与640差0.5；这样就对齐了。这样子处理后，要想几何中心对齐，意味着3×3图像中间元素(u=1.5)要和5×5图像中间元素(u=2.5)重合，按照前面的计算公式，$u=j\ast w1/w2;$ 正好可以得到3×3图像中间元素(u=1.5)在5×5图像中的坐标为2.5，对齐了。

到目前为止，我们通过转换坐标系的原点，使得原图像与输出图像几何中心能够对齐，但是还存在一个小问题。那就是我们的计算机存储图像都是从坐标0开始，我们以0.5作为起始点的坐标体系，在计算机这里是不兼容的，所以，当我们计算得到2.5以后，还需要再进行一个坐标转换，将坐标转为从0开始。这同样很好处理，对得到的结果减0.5即可(2.5-0.5=2)。

最终，我们的映射公式改为如下：

// 原来是这样 float u = j*w1/w2; float v = i*w1/w2; // 现在改为这样 float u = (j+0.5)*w1/w2 - 0.5; float v = (i+0.5)*w1/w2 - 0.5; 

至此，几何中心不对齐的问题得到解决，回顾一下我们的方法，整个流程如下：