mendelow模型_proe凸包怎么画

凸分析中经常见到这些概念，目前这方面的中文资料似乎不太多，决定写篇博客总结一下。

1. 凸包 convex hull

凸包在文献中比较常见些，也称作凸包络面 convex envelope。凸包一般针对某个集合（函数也可以有凸包，但我看到一些文献将函数的凸包称作凸包络面 convex envelope）。

凸包的定义为：对于某个有限集合 { v 1 , v 2 , … , v n } \{v_1, v_2, \dots, v_n\} {
v1​,v2​,…,vn​}，它的凸包为

conv { v 1 , v 2 , … , v n } = { θ 1 v 1 + θ 2 v 2 + ⋯ + θ n v n ∣ θ i ≥ 0 , ∑ n θ i = 1 , ∀ i } \textbf{conv}\{v_1, v_2, \dots, v_n\}=\{\theta_1v_1+\theta_2v_2+\dots+\theta_nv_n|\theta_i\geq 0, \sum^n \theta_i=1, \forall i\} conv{
v1​,v2​,…,vn​}={
θ1​v1​+θ2​v2​+⋯+θn​vn​∣θi​≥0,∑n​θi​=1,∀i}

在学术文献中，符号 $\text{conv}$ 表示凸包。

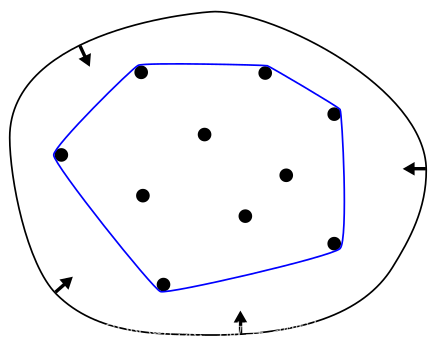
凸包的几何意义为一个集合内所有元素的凸组合，也等价于包含集合元素的所有凸集的交集。例如，下面的图形中，黑点表示集合的每个元素，图中的蓝线为该集合的凸包

• 因为是有限个元素的凸组合，凸包总是有界的

2. 图上方 epigraph

图上方 epigraph 是针对函数的，图上方的几何意义就是指一个函数图形上面的元素集合。函数 $f$ 的图上方的标准定义为：

$$\text{epi }f=\{(x,t)|t\ge f(x),x\in \text{dom }f\}$$

其中，符号 $\text{epi}$ 表示图上方，而 $\text{dom}$ 表示定义域的意思。

上面的图形中，曲线为函数 $f$，它上面的阴影部分就是它的图上方。关于函数图上方与函数凸性有一个重要性质：

• 一个函数为凸函数，当且仅当它的图上方为凸集。

还有一个图下方，英文叫做 hypograph。

3. 凸低估计量 convex underestimator

我没查到权威文献中对凸低估计量的定义，但它的涵义是：在定义域 $f$ 内每个元素上，都比函数 $f$ 小的凸函数。即：

$$g(x)\le f(x)\text{ and g(x) is convex}$$
因此，凸低估计量可以有很多个，例如：

上面的图形中，阴影部分为图上方，而图形中的粗实线函数，与下面的虚线函数，都是函数 $f(x)$ 的低估计量

4. 凸包络面 convex envelope

有时又称为下凸包络面 lower convex envelope。凸包络面与凸包非常像，但我觉得一般分析函数时称为凸包络面，分析集合时称凸包。

一个函数的凸包络面为它的低估计量中最大的，或者为它的图上方的凸包。标准的定义为
g ( x ) = inf ⁡ { t ∣ ( x , t ) ∈ conv   epi   f } g(x)=\inf\{t|(x,t)\in\textbf{conv }\textbf{epi } f\} g(x)=inf{
t∣(x,t)∈conv epi f}

等价为：
g ( x ) = sup ⁡ { g ( x ) ≤ f ( x )  and  g ( x )  is convex } g(x)=\sup\{g(x)\leq f(x) \text{ and $g(x)$ is convex}\} g(x)=sup{
g(x)≤f(x) and g(x) is convex}

在上一个图形中，那条粗实线函数就是 $f(x)$ 的凸包络面(线）¹²。

今天的文章mendelow模型_proe凸包怎么画分享到此就结束了，感谢您的阅读。