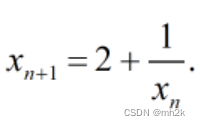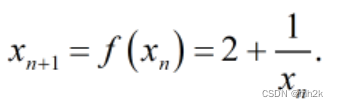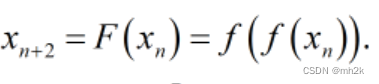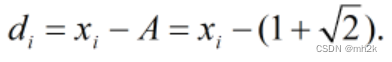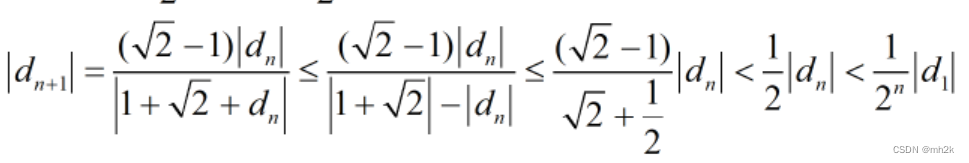裴礼文数学分析-学习笔记（证明递推数列收敛的若干方法）

本文将以书中66页的题为例，探讨证明递推数列收敛的若干方法，以及如何利用数列图像对方法进行深刻理解与掌握。

题面

分析： 

          观察数列特征，不难推出数列相邻两项的递推关系：

        在严格证明该数列收敛前，不妨先设{
}收敛于，由方程,求解出

显然有 0″>，故.

先挖掘一下该数列的基本信息。

首先是上下界，我们常用归纳法得出

其次是单调性，计算前几项的值单调性不明显，通过进一步分析可以发现该数列的奇数项严格单调，偶数项严格递减。（详细见下文）

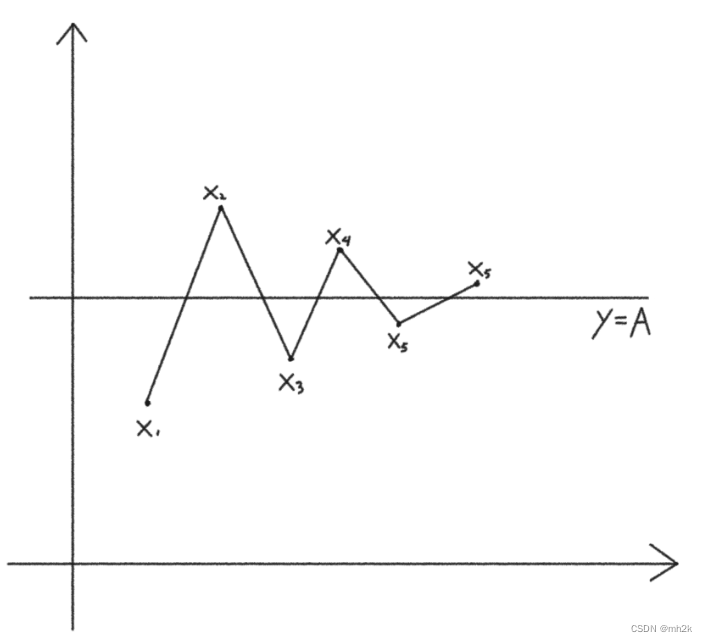
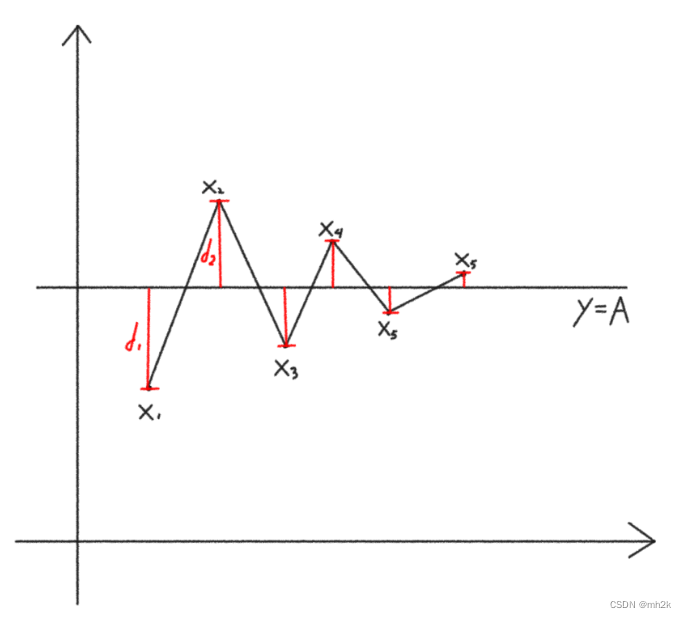
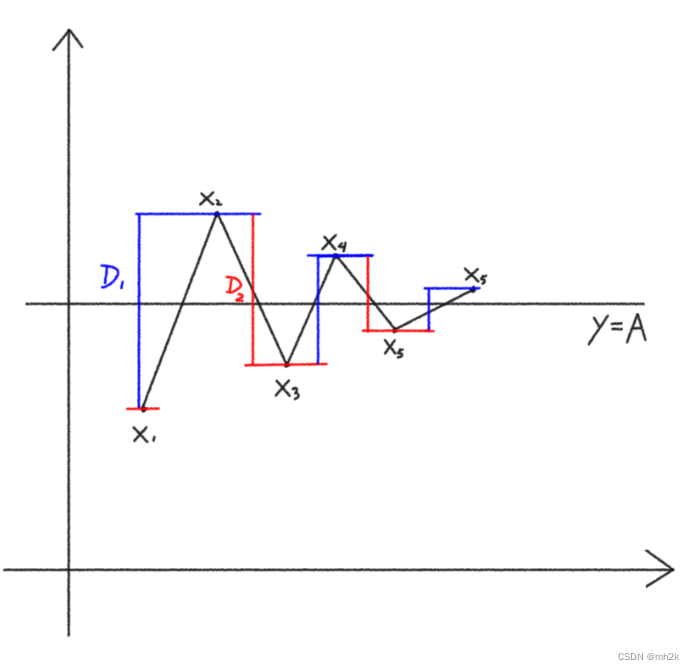
最后有了数列的取值范围和单调性，以及先前求得的极限,就可以绘制出数列大致的图像

（这里为了方便观察，夸大了两项的间距，没有按照真正的数值作画）

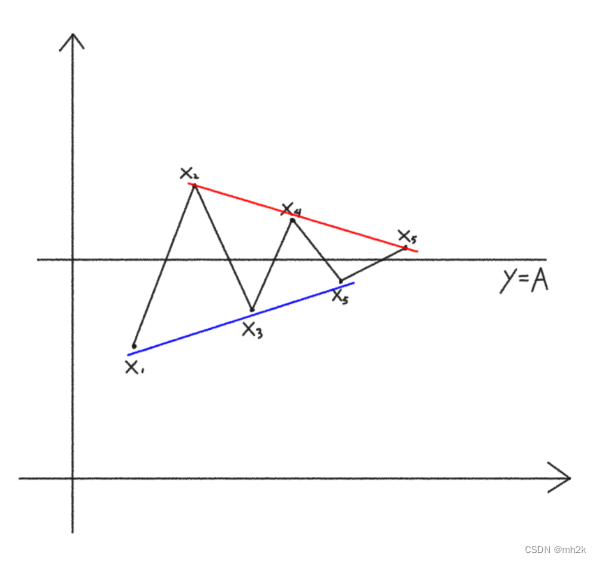
有了图像的直观体会，思路一下就打开了。将奇数偶数项分别连线，

       问题自然地转化为 证明奇偶子列同收敛于A， 而数列的上下界已经找到，由单调有界定理，我们只需严格证明图中所示的单调性，

       由此引出第一种求解递推数列极限的方法——应用单调性。

应用单调性 

知识要点：

分析：

       回顾例题，将递推关系写作映射

       显然严格递减，故对应要点2所述情况，这与先前的图像是相符的，接下来回到如何证明单调性的问题

       要研究相隔一项的单调性，不妨先写出其两项的映射关系

由于具有反序性，则具有保序性，由要点1的结论，就可以得出{
}，{
}的单调性

接下来给出完整证明。 

证明过程 ：

以上就是应用单调性证明数列收敛的方法 

       我们再次回到先前的图像

       这次我们换一个角度，观察各点与极限A的差值（，，…），发现其绝对值是不断递减并趋于零的，如何用数学语言对这个发现进行刻画，并将其用于我们的证明呢？

       由此引出第二种方法——替换与变形

替换与变形 

分析：

        将上文提到的插值表示出来

       若能证明 ，则自然得证。

       而我们发现{
}总是在轴上下来回跳动，这与{
}在上下来回跳动一样，是难于直接用于证明的。

       但通过图像发现单调递减，并趋于0，若观察到的单调性得以验证，则说明其收敛，再结合递推关系得出，从而.

证明过程：

该证明延续之前分析思路，也可参考书中更简洁的证法

       又双叒回到之前的图像

       新的角度，观察相邻两项的差值（,,…）， 和之前相似，我们观察到其绝对值是单调递减趋于零的

       这很难不让人联想到压缩映像原理。 

压缩映像原理

定理及其证明：

 没什么好分析的，结合先前得到的上下界，直接利用定理进行证明。

证明过程

小结 

该题的递推形式不是很难，但通过对其图像不同角度的解读，比较自然地发掘出了以上三种解法。这启示我在面对难题无从下手时，可以先绘制出图像，将抽象的关系化作一种整体的观感，并思考如何严谨刻画图像中的显然，这或许能帮助我们找到难题的突破口。证明递推数列收敛还有许多方法，需要一些时间去整理，日后再更吧。

今天的文章裴礼文数学分析-学习笔记（证明递推数列收敛的若干方法）分享到此就结束了，感谢您的阅读。