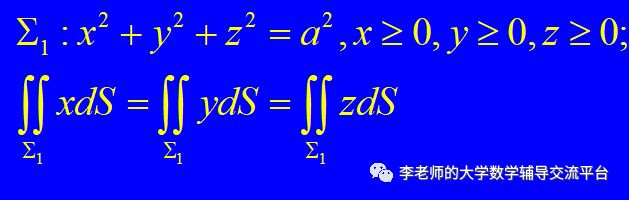二重积分被积函数的奇偶性总结_二重积分被积函数的奇偶性总结

      我们在高等数学中，学习了定积分、二重积分、三重积分、曲线积分、曲面积分。其中奇偶对称性、轮换对称性，一定要好好理解和体会，切不可混淆两种对称性。

      定积分、二重积分、三重积分、第一类曲线积分、第一类曲面积分，都用到了奇偶对称性、轮换对称性。

下面以第一类曲面积分进行讨论：

下面举例说明，如何应用上面的理论进行解题：

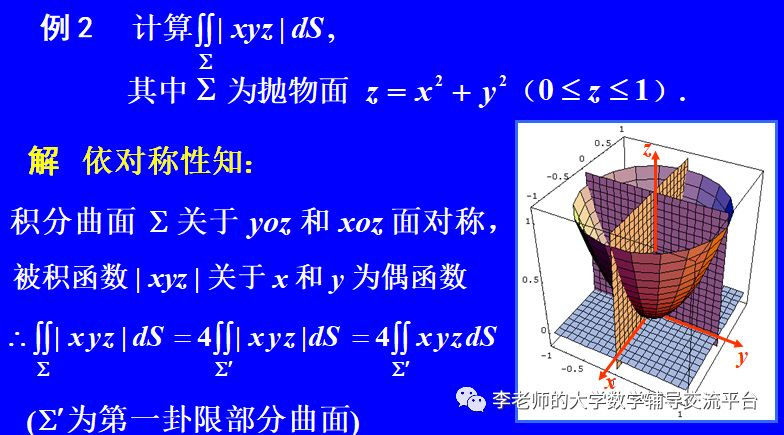
上面这个例题，很容易判断关于x,y,z都是偶函数。但区域仅仅关于yoz、xoz面对称。因此用了2次奇偶对称，变为4倍的第一卦限的积分。

再举个例子：

分析：

本题的A，左边的被积函数关于x为奇函数，而积分曲面关于yoz对称，因此左边=0；

选项B，左边的被积函数关于y为奇函数，而积分曲面关于xoz对称，因此左边=0；

选项D，左边的被积函数关于y(或X)为奇函数，而积分曲面关于xoz(或yoz)对称，因此左边=0；

对于选项C来说，左边被积函数关于Z为奇函数，但积分曲面关于XOY不对称，因此不能采用这种方式。

注意：

选项C中的f(x,y,z)=z，没有字母X，因此关于X为偶函数，而积分曲面关于YOZ对称，这样上半球面的后侧与前侧合并为2倍的前侧曲面积分；

再就是f(x,y,z)=z中没有字母Y，因此又关于Y为偶函数，而积分曲面关于XOZ对称，这样积分曲面的左侧和右侧，再一次合并为2倍的右侧(即第一卦限的曲面)，因此结果为4倍的第一卦限的积分。

再次注意，这里的被积函数还是f(x,y,z)=z,而积分曲面为第一卦限的球面，显然曲面方程关于字母X、Y、Z具备了轮换对称性，因此在第一卦限对被积函数Z的曲面积分=被积函数X的曲面积分=被积函数Y的曲面积分。即：

所以选项C是正确的。

上面的理论，一定要好好体会和理解，熟练掌握该知识点，对于这类题，具有事半功倍的效果。