快速排序算法演示_中序遍历的时间复杂度

快速排序

给定一个序列：22 33 49 47 33' 12 68 29

进行快速排序

主要思想

• 从序列中，任选一个记录k作为轴值 pivot

  选择策略：

  • 第一个元素
  • 最后一个元素
  • 中间元素
  • 随机选择

• 将剩余的元素，分割成 左子序列 L 和 右子序列 R

• L 中所有元素都 < k， R 中所有元素都 > k

• 对 L 和 R递归进行快排，直到子序列中有 0 个 或者 1 个元素，退出

图解

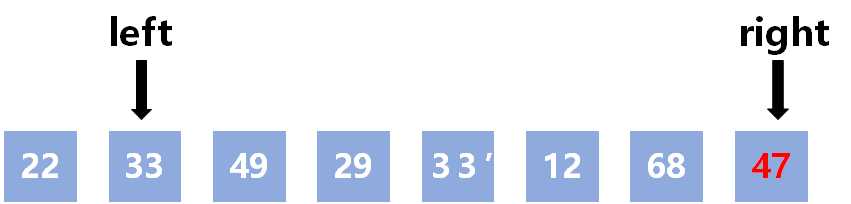
初始数组：

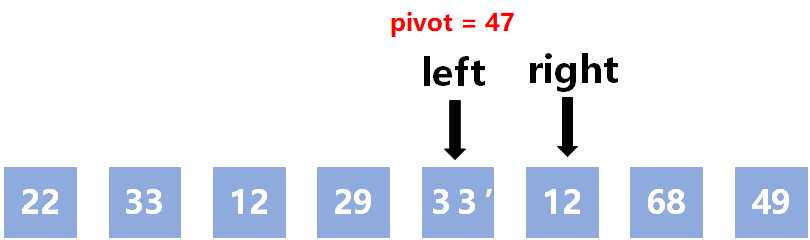
选定47为轴值pivot

pivot与最后一个值29进行交换（把pivot放到最后面）

接下来，以pivot=47为界，分成左子序列 L和右子序列 R

比47大的都放在右边，比47小的都放在左边（用的交换）

遍历数组

• 两个指针left和right
• 当left != right的时候
  • 若arr[left]的，小于等于pivot，且left < right的时候，left右移
    • 如果left和right未相遇，把left的值赋给right对应的值
    • arr[right] = arr[left]
    • left指针停止移动，轮到right移动
  • 当arr[right]的值，大于等于pivot，且right > left的时候，right左移
    • 如果left和right未相遇。把right的值赋给left对应的值
    • arr[left] = arr[right]
    • right指针停止移动，轮到left移动
• 注意：轴值用pivot保存

第一轮分割序列

pivot=47和最后一个值互换

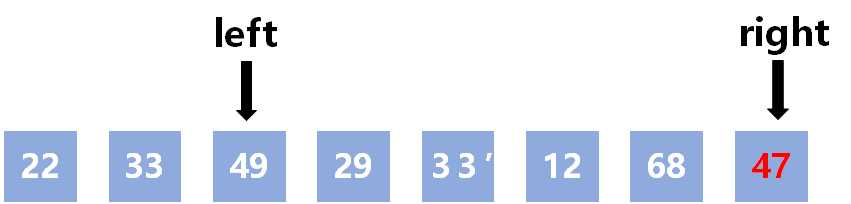
22 <= 47，left向右移动

33 <= 47，left向右移动

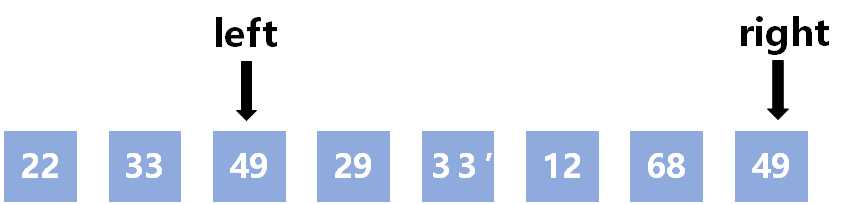
49 > 47，不满足arr[left] <= pivot

把left的值赋给right

arr[right] = arr[left]

赋值过后，left不动，right向左移动

68 >= 47，right向左移动

12 < 47，不满足arr[right] >= pivot

把right的值赋给left

arr[left] = arr[right]

赋值过后，right不动，left向右移动

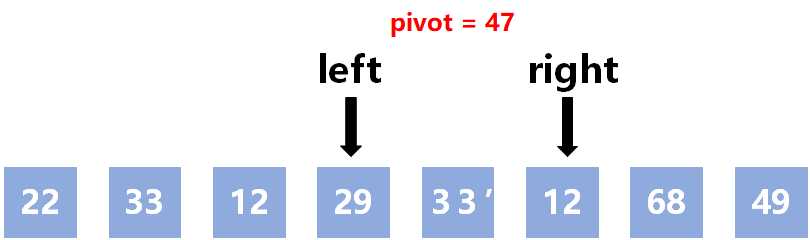
29 < 47，left向右移动

33' < 47，left向右移动

向右移动后，left == right，退出循环

将pivot赋给arr[left]

至此，第一轮分割序列完成

第二轮分割序列 — 左子序列

经过第一轮分割，47左边的是左子序列，右边是右子序列

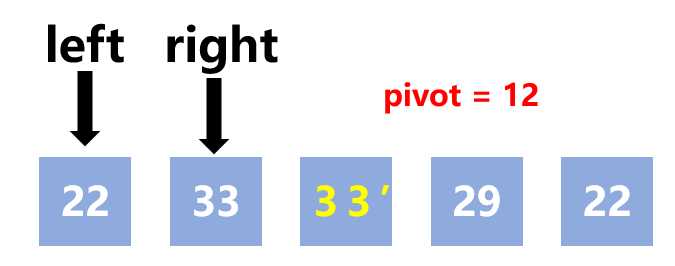
第二轮对左子序列分割，选择中间值作为pivot

12和33'进行交换

22 > 12，不满足arr[left] <= pivot

把arr[left]赋给arr[right]

arr[right] = arr[left]

赋值过后，left不动，right向左移动

29、33'、33都比12大，所以right一直移动到下图位置

33 > 12,right继续向左移动

此时right == left，终止循环

把pivot赋给arr[left]

至此，左子序列1也分割完成了

小结

快排就是一个递归的过程，分割得到左子序列

再对左子序列进行快排分割，得到左子序列的左子序列…

处理完左边，再去处理右边的右子序列

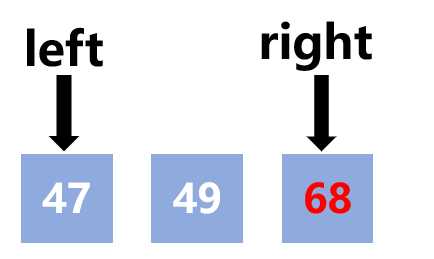
第三轮分割序列 — 右子序列

右子序列只有47、68、49，选择48作为轴值 pivot

pivot和最后一个值交换

47、49都比pivot=68小，left一直向右移动，直到left == right

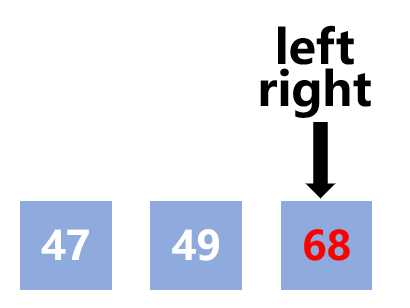
分割之后，只剩下左子序列：47、49

47、49，选49作为轴值，得到左子序列47

子序列只剩下一个元素47，就不必排序了，右边排序结束

结果：47、49、68

C++实现

选择中间的值作为轴值

#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#include <string>
#include <stack>
#include <cmath>
#include <map>

using namespace std;


/** * * @param arr 待分割的序列 * @param left 左边界 * @param right 右边界 * @return 分割后轴值的位置 */

template<class T>
int PartitionArr(vector<T>& arr, int left, int right) { 
   
    T temp = arr[right];
    while (left != right) { 
   
        while (arr[left] <= temp && left < right) { 
   
            left++;
        }
        if (left < right) { 
   
            arr[right] = arr[left];
            // 赋值后，left不动，right向左移
            right--;
        }
        while (arr[right] >= temp && right > left) { 
   
            right--;
        }
        if (left < right) { 
   
            arr[left] = arr[right];
            // 赋值后，right不动，left向右移
            left++;
        }
    }
    // 当left == right，把轴值放回left上
    arr[left] = temp;
    return left;
}

/** * * @param arr 待排序数组 * @param left 左边界 * @param right 右边界 */
template<class T>
void quickSort(vector<T>& arr, int left, int right) { 
   
    // 子序列剩下0或1个元素，排序结束
    if (right <= left) { 
   
        return;
    }

    // 选择数组中间作为轴值
    int pivot = (left + right) / 2;
    // 把轴值放到数组最后面
    swap(arr[right], arr[pivot]);
    // 分割后轴值的位置
    // 分割后，左边值 < 轴值 < 右边值
    pivot = PartitionArr(arr, left, right);
    quickSort(arr, left, pivot - 1);
    quickSort(arr, pivot + 1, right);
}


int main() { 
   
    vector<int> arr = { 
    22,33,49,47,33,12,68,29 };
    for (auto& i : arr) { 
   
        cout << i << ' ';
    }

    cout << endl << endl;

    quickSort(arr, 0, arr.size() - 1);

    for (auto& i : arr) { 
   
        cout << i << ' ';
    }

    cout << endl << endl;
    system("pause");
    return 0;
}

总结

• 快排是不稳定的排序算法

  • 33 33'排序后可能变成33' 33

• 时间复杂度：

  • 平均：$O(Nlo{g}_N)$
  • 最差：$O(N^2)$，退化为冒泡排序

• 空间复杂度：

  • 递归调用消耗栈空间
  • 最优：$O(lo{g}_N)$
  • 最差：$O(N)$，退化为冒泡排序

如有错漏不实之处，欢迎补充纠正。

今天的文章快速排序算法演示_中序遍历的时间复杂度分享到此就结束了，感谢您的阅读。