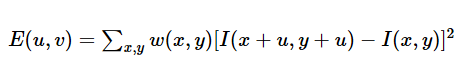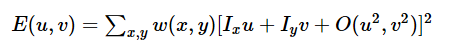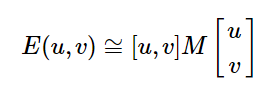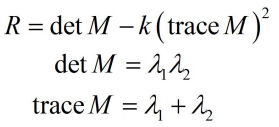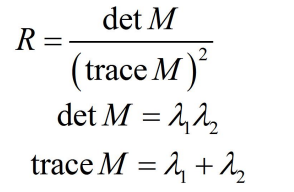harris角点检测算法的原理_harris角点检测算法的原理

文章目录

一、harris角点检测原理

1.1基本思想

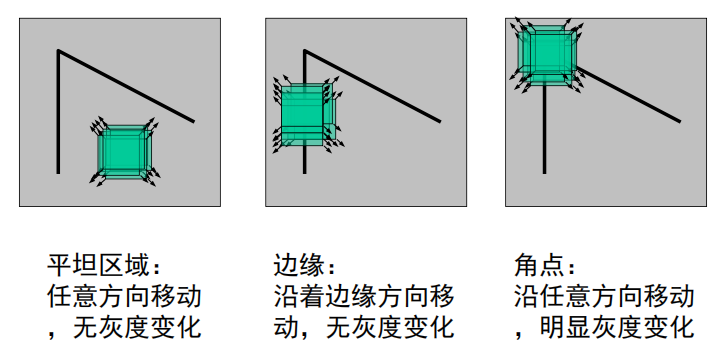
使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。

1.2 数学模型

图像窗口平移[u,v]产生灰度变化E(u,v)为：

上式经泰勒展开后的得到

对局部微小的移动量 [u,v]，所以可以近似得到下式

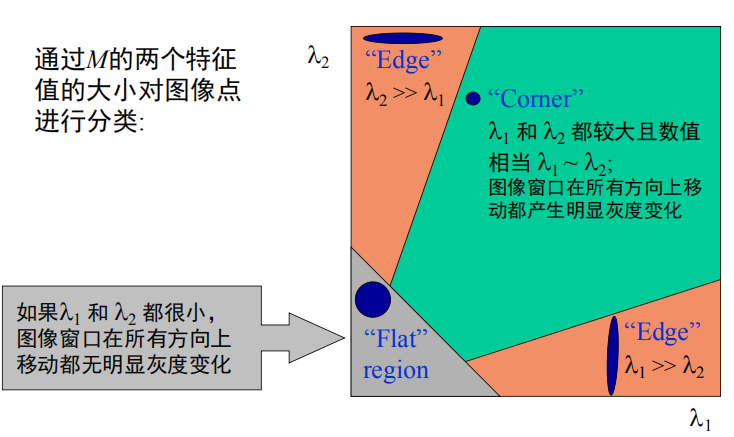
记M的特征值λ1、λ2，可以将图像上的像素点分类成直线、平面与角点：当λ1和λ2 都比较大，且近似相等时，可以认为是角点。对图像点分类如下图：

3、关于harris角点响应函数R

由于是通过M的两个特征值的大小对图像进行分类，所以，定义角点相应函数R：

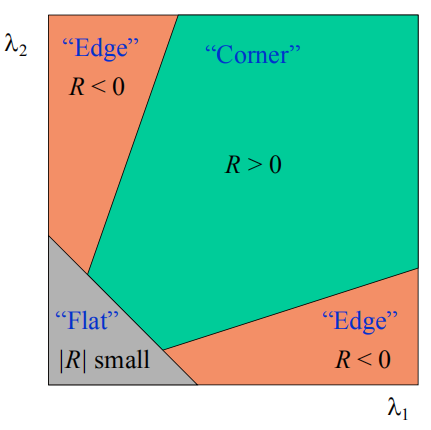
于是上图图像点分类图转化为下图：

有结论如下：

角点——R为大数值正数
边缘——为大数值负数
平坦区——为小数值

在判断角点的时候，对角点响应函数R进行阈值处理：R > threshold，提取R的局部极大值。

二、harris角点检测源代码

2.1 计算harris角点响应函数R

算法：

使用高斯倒数滤波器计算图像x,y两个方向的梯度值im_x,im_y（使用高斯倒数滤波器计算可在角点检测过程中抑制噪声强度）
计算图像两个方向梯度的乘积分别为x方向的平方，y方向的平方，x和y的乘积，同样使用高斯倒数滤波器计算
计算局部特征结果矩阵M的特征值
计算响应函数的值

def compute_harris_response(im, sigma=3):
    '''
    对每个像素值计算Harris角点检测器响应函数
    :param im:
    :param sigma:
    :return:
    '''

    # 计算导数
    im_x = np.zeros(im.shape)
    im_y = np.zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (0, 1), im_x)
    filters.gaussian_filter(im, (sigma, sigma), (1, 0), im_y)

    # 计算Harris矩阵分量
    Ixx = filters.gaussian_filter(im_x * im_x, sigma)
    Ixy = filters.gaussian_filter(im_x * im_y, sigma)
    Iyy = filters.gaussian_filter(im_y * im_y, sigma)

    # 计算特征值和迹
    Idet = Ixx * Iyy - Ixy ** 2
    Itrace = Ixx + Iyy

    #return Idet / Itrace
    print  Idet - 0.04 * (Itrace ** 2)
    return Idet-0.04*Itrace**2

2.2harris角点检测

伪代码：

输入图像，并将图像转换为灰度图
对图像检测harris角点
画出Harris响应图
选取像素值高于设定阈值的点，并进行局部极大值抑制
输出图像的角点

# 读入图像
im0 = array(Image.open('data/7/IMG_20200106_175418.jpg'))
im = array(Image.open('data/7/IMG_20200106_175418.jpg').convert('L'))

# 检测harris角点
harrisim = compute_harris_response(im)


# Harris响应函数
harrisim1 = 255 - harrisim

figure()
gray()

#画出Harris响应图
subplot(151)
title("原图",fontproperties=font)
axis('off')
imshow(im0)
subplot(152)
imshow(harrisim1)
print harrisim1.shape
axis('off')
axis('equal')

#设定阈值以及限制并输出
threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
    filtered_coords = harris.get_harris_points(harrisim, 6, thres)
    subplot(1, 5, i+3)
    imshow(im)
    print im.shape
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
    axis('off')
    
show()

局部极大值限制原理为，角点之间的距离必须大于设定的最小距离，这样若有过近或重叠的角点，会被滤除。

三、harris角点响应函数R的分析

3.1不同k值

k=0.01

图像角点结果：

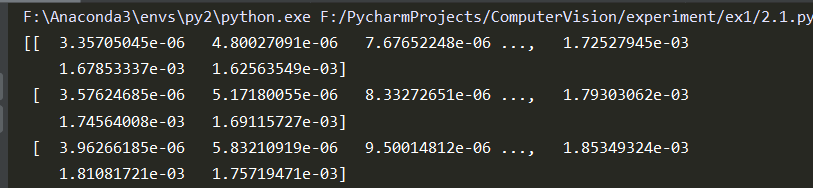
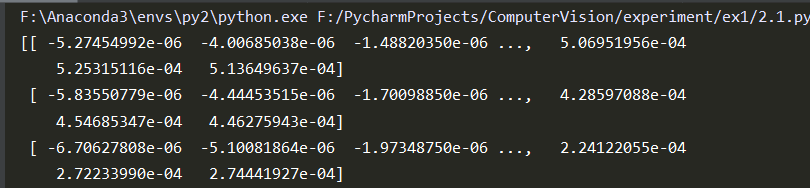
R值结果：

k=0.04

图像角点结果：

R值结果：

k=0.06

图像角点结果：

R值结果：

k=0.08

图像角点结果：

R值结果：

分析：
K值越小，检测到的角点越多，R值趋于小数值，随着K值的增大，检测到的角点减少，响应函数R值较小，R值趋于负数，因为在R=detM-k(traceM)^2中，若k值较小，则R值由主要由detM=λ1λ2值决定，此时λ1λ2都较大，则R值大，大于局部极大值的角点多，所以取到的角点多；若k值较大，k(traceM)的平方值增大，R值变为大值负数，较多角点受局部极大值抑制，取到的角点少一些。所以k值取0.04-0.06为宜。

3.2对R不同的计算方法

3.2.1 函数计算

图像角点结果：

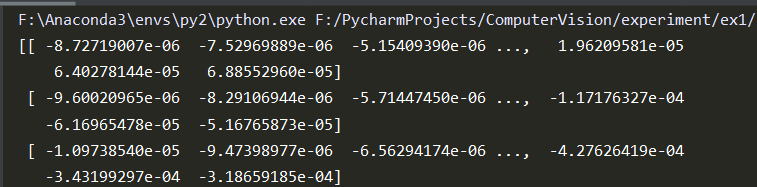
R值结果：

3.2.2 商计算

图像角点结果：

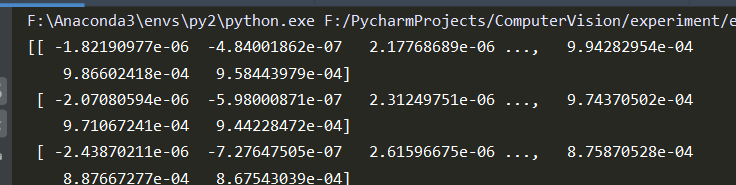
R值结果：

分析：
由上面讨论的结果可知，在R=detM-k(traceM)^2中响应值R受K值大小影响，检测出的角点变化明显。上图结果可知，返回商计算结果时，更易于检测出边缘角点，而返回函数 R=detM-k(traceM)^2结果时，并没有检测出图像中的边缘角点，因此函数计算出的边缘像素点的R值大多被局部极大值抑制导致边缘角点被滤掉。所以，为避免R值易受K值影响，最好采用返回R值的商计算结果。