计算机图形学中消隐的相关概念及算法是_Bresenham算法

本文整理自西安交通大学软件学院祝继华老师的计算机图形学课件，请勿转载

基本概念

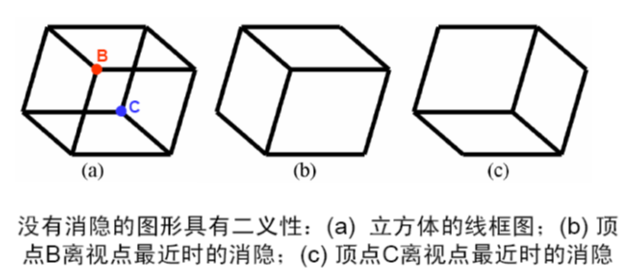
投影变换失去了深度信息，往往导致图形的二义性

• 消隐：为了消除二义性，必须在绘制时消除被遮挡的不可见的线或面，习惯上称作消除隐藏线和隐藏面；
• 经过消隐得到的投影图称为物体的真实图形
• 消隐结果与观察物体有关，也与视点有关

提高消隐算法效率的常见方法

• 利用连贯性
• 包围盒技术
• 背面剔除
• 空间分割技术
• 物体分层表示

利用连贯性

相邻事物的属性之间有一定的连贯性，其属性值通常是平缓过渡的，如颜色值、空间位置关系等

• 物体连贯性
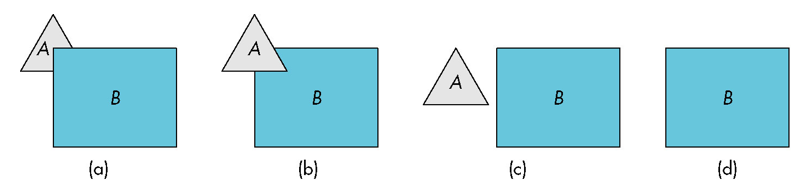
  • 如果物体A与物体B是完全相互分离的，则在消隐时，只需比较A、B两物体之间的遮挡关系就可以了，无须对它们的表面多边形逐一进行测试。
• 面的连贯性
  • 一张面内的各种属性值一般都是缓慢变化的，允许采用增量形式对其进行计算。
• 扫描线的连贯性
  • 相邻两条扫描线上，可见面的分布情况相似。
• 区域连贯性
  • 区域指屏幕上一组相邻的像素，它们通常为同一个可见面所占据，可见性相同。
  • 区域连贯性表现在一条扫描线上即为扫描线上的每个区间内只有一个面可见。
• 深度连贯性
  • 占据屏幕上同一区域的不同表面的深度不同；
  • 但同一表面上的相邻部分深度是相近的，在判断表面间的遮挡关系时，只需取其上一点计算出深度值，比较该深度值即可得到结果。

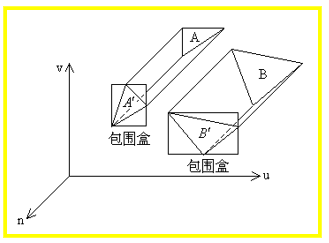
包围盒技术

定义:一个形体的包围盒指的是包围它的简单形体

好的包围盒要具有两个条件：

• 假设包围和充分
• 紧密包围着形体；
• 对其的测试比较简单。
• 常用包围盒:长方体、球、圆柱；

例如：两个空间多边形A、B在投影平面上的投影分别为A’，B’ ，因为A’ 、B’的矩形包围盒不相交，则A’、B’不相交，无须进行遮挡测试。

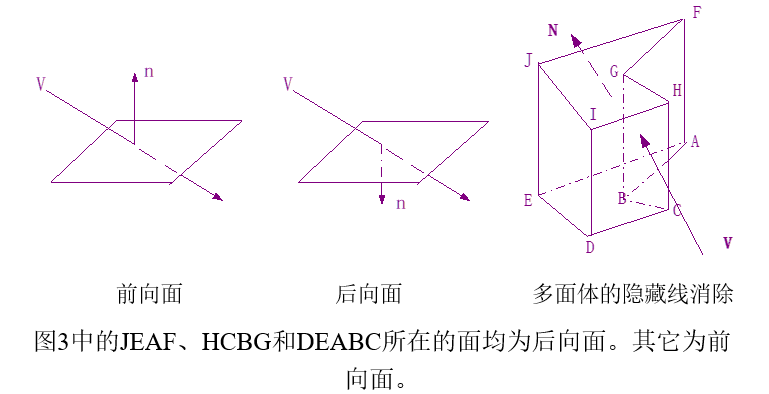
背面剔除

• 外法向：规定每个多边形的外法向都是指向物体外部的。
• 前向面：若多边形的外法向与投影方向（观察方向）的夹角为钝角（V· N<0），称为前向面。
• 后向面：若多边形的外法向与投影方向（观察方向）的夹角为锐角（V· N>0），称为后向面（背面）。

后向面总是看不见的，不会由于后向面的遮挡，而使别的棱成为不可见的。因此计算时，可以把这些后向面全部去掉，这并不影响消隐结果

空间分割技术

场景中的物体，它们的投影在投影平面上是否有重叠部分？

• 依据：对于根本不存在相互遮挡关系的物体，应避免这种不必要的测试。
• 原因：物体在场景中分散，有些物体的投影相距甚远，不存在遮挡关系。
• 方法：将投影平面上的窗口分成若干小区域；为每个小区域建立相关物体表，表中物体的投影于该区域有相交部分；则在小区域中判断那个物体可见时，只要对该区域的相关物体表中的物体进行比较即可。

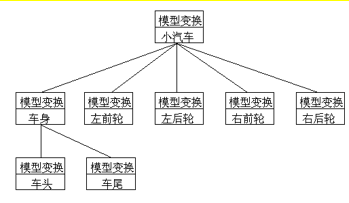
物体分层表示

表示形式：模型变换中的树形表示方式；

• 依据：减少场景中物体的个数，降低算法复杂度；
• 将父节点所代表的物体看成子节点所代表物体的包围盒，当两个父节点之间不存在遮挡关系时，就没有必要对两者的子节点做进一步测试；
• 父节点之间的遮挡关系可用包围盒进行预测试。

消隐的分类

按消隐对象和输出结果分类

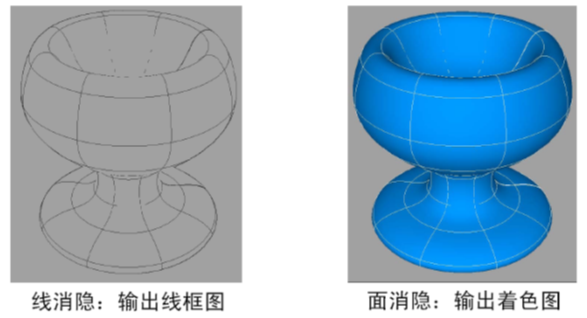
• 线消隐：消除的是物体上不可见的边。
• 面消隐：消除的是物体上不可见的面。

根据消隐空间分类

• 物体空间的消隐算法：以场景中的物体为处理单元；

  for (场景中的每一个物体)

  ​ {将其与场景中的其它物体比较，确定其表面的可见部分；显示该物体表面的可见部分；}

  

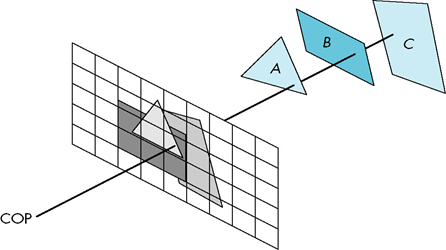
• 图像空间的消隐算法：以窗口内的每个像素为处理单元；

  for(窗口内的每一个像素)

  {确定距视点最近的物体，以该物体表面的颜色来显示像素}

  

消除隐藏线

坐标变换：通过坐标变换，将视点变换到Z轴的正无穷大处，视线方向变为Z轴的负方向

最基本的运算：线消隐中，判断面对线的遮挡关系：体分解成面，再判断面与线关系。判断过程中需反复地进行线线、线面之间的求交运算。

平面对直线段的遮挡判断算法

1. 若线段的两端点及视点在给定平面的同侧，线段不被给定平面遮挡，转(7)；
2. 若线段的投影与平面投影的包围盒无交，线段不被给定平面遮挡，转(7)；
3. 求直线与相应无穷平面的交：
   • 无交点转(4)；
   • 若交点在线段内部，交点将线段分成两段，与视点同侧一段不被遮挡，另一段在视点异侧转(4)；
   • 若交点在线段外部,转(4)。
4. 求所剩线段的投影与平面边界投影的所有交点。若无交点，转(7)。
5. 以上所求得的各交点将线段的投影分成若干段，求出第一段中点。
6. 若第一段中点在平面的投影内，则相应的段被遮挡，否则不被遮挡；其他段的遮挡关系可依次交替取值进行判断。
7. 结束。

基本数据结构

面表(存放参与消隐的面) +线表(存放待显示的线)

消除隐藏面

• 画家算法
• Z缓冲算法
• 扫面线Z缓冲算法
• 区间扫面线算法
• 区域子分割(Warnack)算法
• 光线投射算法

今天的文章计算机图形学中消隐的相关概念及算法是_Bresenham算法分享到此就结束了，感谢您的阅读。