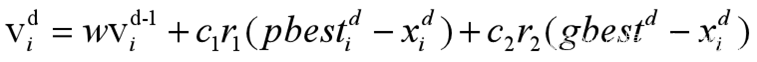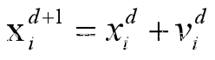粒子群最优化_粒子群算法MATLAB

粒子群最適化（Particle Swarm Optimization、PSO）是一种进化算法，通过模拟鸟群的捕食行为而设计出来的。从随机解开始，通过迭代来寻找最优解，并通过适应度评估解的质量。

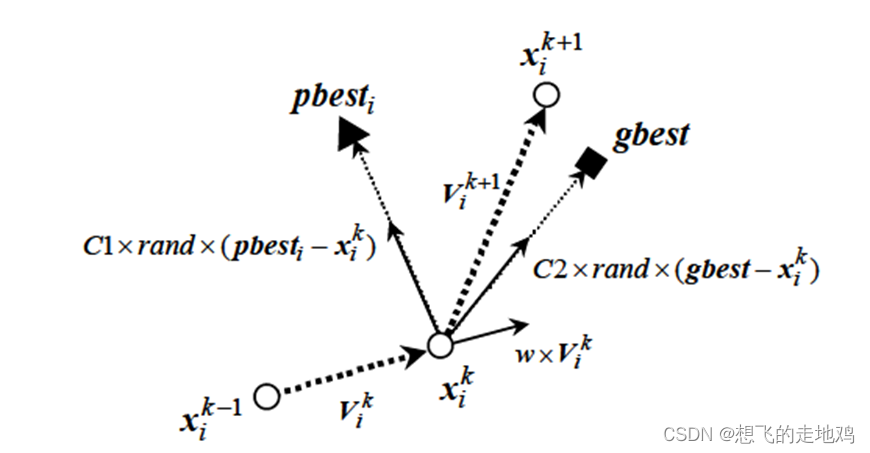
如果将最优化问题视为在空中寻找食物的鸟群，那么粒子群最优化问题的潜在解就是探索空间中的鸟，也称为“粒子”，而“食物”是最优化问题的最优解。每个粒子都有一个由最优化问题确定的适应度，用于评估粒子的“好坏”程度。每个粒子都有速度，决定了它的飞行方向和距离，它会根据自己的飞行经验和同伴的飞行经验来调整自己的飞行。

粒子群被初始化为一群随机粒子（随机解），然后通过迭代来寻找最优解。在每次迭代中，粒子通过跟踪两个“极值”来更新自己，第一个是粒子自己经历的最佳位置，即个人极值（pbest），另一个是整个群体经历的最佳位置，即全局极值（gbest）。每个粒子都会通过这两个极值不断地更新自己，并生成下一代群体。

粒子”（Particle）i的第d维速度更新式：

 「粒子」（Particle）i的第d次元位置更新公式：

 c 1和c 2是粒子群最適化中的两个参数，它们分别称为个体学习因子和社会学习因子。c 1的值越大，粒子越倾向于向其个体最佳位置移动。c 2的值越大，粒子越倾向于向整个群体的最佳位置移动。

PSO算法的步骤如下：

〔Step 1〕 使用随机数初始化个体的位置xi和速度Vi。 〔Step 2〕 评估要最小化的目标函数值f(xi)。 〔Step 3〕 将f(xi)与个体之前的最佳值f(pbesti)进行比较。如果f(xi) < f(pbesti)，则更新f(pbesti) = f(xi)和pbesti = xi。 〔Step 4〕 将f(xi)与群体中的最佳值f(gbest)进行比较。如果f(xi) < f(gbest)，则更新gbest = xi。 〔Step 5〕 使用公式（1）更新速度，使用公式（2）更新位置。 〔Step 6〕 返回到Step 2，重复执行直到满足收敛条件。

实验设计：

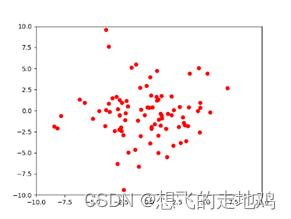
目标函数：z = x^2+y^2 (-10<=x,y<=10) 寻找最优解 初始粒子群：随机生成一组粒子的位置和速度 最终结果：所有粒子基本上都收敛到了(0,0)点。

 代码：

import numpy as np
import random
import matplotlib.pyplot as plt


class PSO():
    # PSO参数设置
    def __init__(self, population_size, step):
        self.w = 0.6
        self.c1 = 2
        self.c2 = 2
        # self.r1 = 0.6
        # self.r2 = 0.3
        self.pN = population_size  # 粒子数量
        self.dim = 2  # 搜索维度
        self.r1 = np.random.rand(self.pN, self.dim)
        self.r2 = np.random.rand(self.pN, self.dim)


        self.step = step  # 迭代次数
        self.X = np.zeros((self.pN, self.dim))  # 所有粒子的位置和速度
        self.V = np.zeros((self.pN, self.dim))
        self.pbest = np.zeros((self.pN, self.dim))  # 个体经历的最佳位置和全局最佳位置
        self.gbest = np.zeros((1, self.dim))
        self.p_fit = np.zeros(self.pN)  # 每个个体的历史最佳适应值
        self.g_fit = 1e10  # 全局最佳适应值

    #目标函数
    def function(self, X):
        # k = [i * i for i in X]
        # return sum(k)
        x1 = X[0]
        x2 = X[1]
        return x1**2 + x2**2
        # return np.sum(np.square(X))

    #初始化种群
    def init_Population(self):
        for i in range(self.pN):  # 因为要随机生成pN个数据，所以需要循环pN次
            for j in range(self.dim):  # 每一个维度都需要生成速度和位置，故循环dim次
                self.X[i][j] = random.uniform(-10, 10)
                self.V[i][j] = random.uniform(0, 1)
            self.pbest[i] = self.X[i]  # 其实就是给self.pbest定值
            tmp = self.function(self.X[i])  # 得到现在最优
            #更新局部最优
            self.p_fit[i] = tmp

            #跟新全局最优
            if tmp < self.g_fit:  # 得到现在最优和历史最优比较大小，如果现在最优大于历史最优，则更新历史最优
                self.g_fit = tmp
                self.gbest = self.X[i]

    def evolve(self):
        # fitness = []
        fig = plt.figure()
        for t in range(self.step):
            for i in range(self.pN):
                temp = self.function(self.X[i])
                # 更新个体最优
                if temp < self.p_fit[i]:
                    self.p_fit[i] = temp
                    self.pbest[i] = self.X[i]
                    if self.p_fit[i] < self.g_fit:  # 更新全局最优
                        self.gbest = self.X[i]
                        self.g_fit = self.p_fit[i]

            #更新数度，位置

            for i in range(self.pN):
                self.V[i] = self.w * self.V[i] + self.c1 * self.r1[i] * (self.pbest[i] - self.X[i]) + \
                            self.c2 * self.r2[i] * (self.gbest - self.X[i])
                self.X[i] = self.X[i] + self.V[i]
            plt.clf()
            plt.scatter(self.X[:, 0], self.X[:, 1], s=30, color='red')
            plt.xlim(-10, 10)
            plt.ylim(-10, 10)
            plt.pause(0.05)


pso = PSO(100, 150)
pso.init_Population()
pso.evolve()
plt.show()

今天的文章粒子群最优化_粒子群算法MATLAB分享到此就结束了，感谢您的阅读。