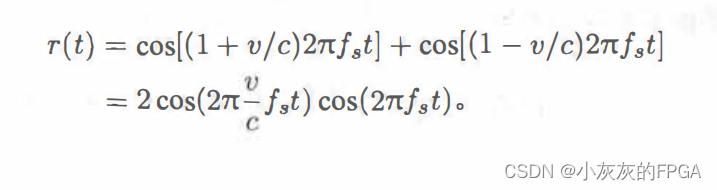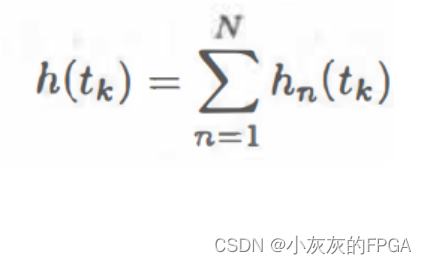多径信道会引起什么现象_最大信道利用率公式

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录

一、多径现象
二、两径模型
1、多普勒效应
2、多普勒频移
三、瑞利衰落
1、瑞利分布
2、莱斯分布
四、选择性衰落
1、时间选择性衰落
2、频率选择性衰落
3、信道衰落的影响

本节内容
一、多径现象
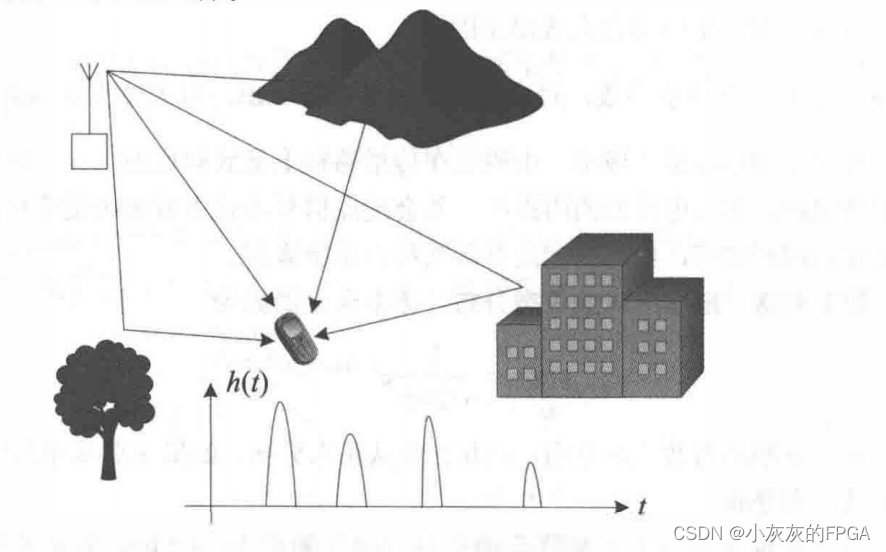
由于传播环境中存在建筑、树木等物体，电磁波从发射机发射出来，经过多个物体的反射从不同的路径到达接收机，这种现象称为多径现象。不同路径的传播距离不同，到达接收机的时间也就不同。若发送一个尖脉冲，接收机会接收一系列的展宽的脉冲。

二、两径模型
1、多普勒效应
多径现象的一个效应是在终端移动的时候引起信道的快衰落。快衰落可以用多普勒效应解释。通常，当火车冲我们开过来时候，汽笛声是比较尖锐的，而当火车远离我们而去，汽笛声是比较沉闷的。由于火车的运动使得汽笛声频率发生变化，来的时候升高，离开的时候降低，也就是多普勒效应。
2、多普勒频移
两个相向运动的物体，相对速度为v,一个物体发出频率fs的波，另一个物体收到的波的频率为fr=(1+v/c)fs，其中c为波的传播速度，光速。对于两径模型，若终端的运动速度为v，收到的两条路径的频率分别为(1+v/c)fs和(1-v/c)fs，两个信号叠加的结果如下：

接收信号r(t)相当于两个余弦函数的乘积，cos(2π(v/c)×fs×t)是变化的信道，频率为(v/c)×fs=v/λ,这个频率称为多普勒频移。
三、瑞利衰落
当终端运动时，路径上的信号频率相同，相位随机，叠加在一起，相互增强或相互抵消，合成一个随机变量，由于相位的快速变化导致信道增益的快速变化，形成快衰落。
1、瑞利分布
射频信号经过的信道，等效成基带的复数信道，第k条路径发生在时刻tk,其基带复数响应为h(tk)，每条路径都是多条微路径叠加而成，因此h(tk)的表达式如下，其中hn(tk)表示每条微路径的复数基带响应。

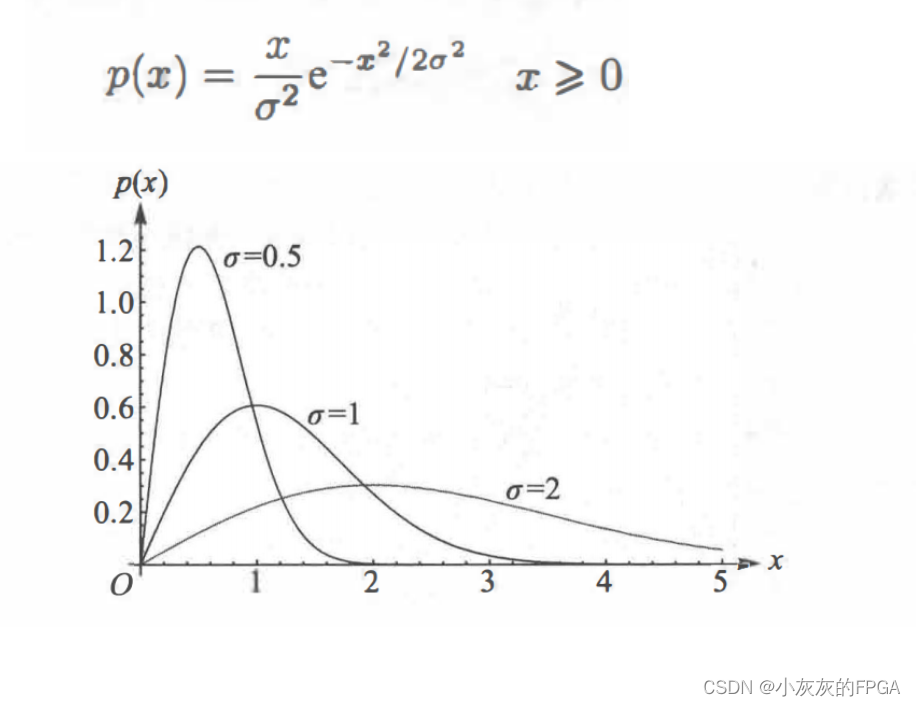
若所有的微路径都是独立同分布的随机变量，由大数定律，叠加的结果hn(tk)服从复高斯分布，它的模|hn(tk)|服从瑞利分布,rayleigh distrubution,相位服从均匀分布，故这种衰落称为瑞利衰落。瑞利分布的概率密度函数表达式及图形如下：

2、莱斯分布
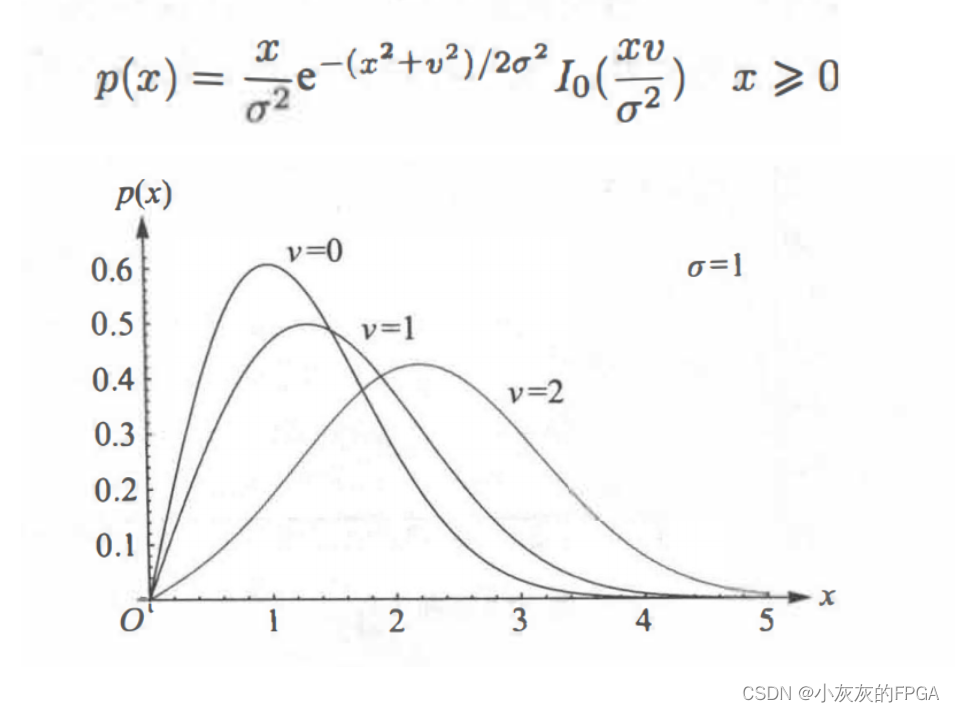
若多个微路径中存在一个幅度比较高的主要分量信号，则|hn(tk)|服从莱斯分布，Rice distribution，其概率密度函数表达式及图形如下：

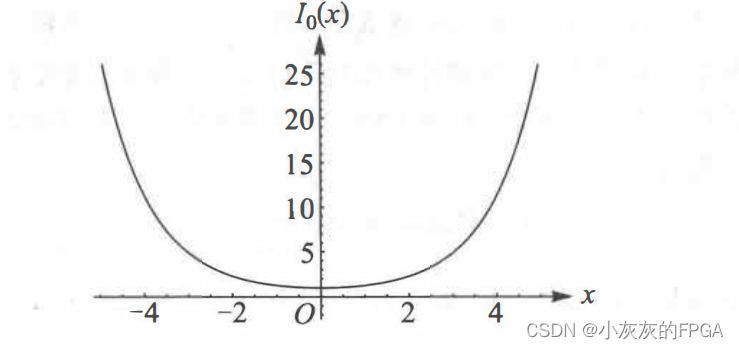
其中I0(x)是修正的第一类零阶贝塞尔函数，其图形如下：

需要注意的是：若v=0，则莱斯分布就退化为瑞利分布；若v比较大的情况下，莱斯分布可近似为高斯分布。
四、选择性衰落
1、时间选择性衰落
相干时间是指信道基本不变的时间，一般用于定性描述。信道变化的频就是多普勒频移，因此多普勒频移越大，信道变化越快。相干时间，与多普勒频移成反比，因为快衰落信道在不同的时间的衰落不一样，故称为时间选择性衰落。
2、频率选择性衰落
相干带宽是指在该带宽内的信道衰落基本不变，并且与信道的冲激响应h(t)的持续时间成反比，也就是所谓的时延扩展。频率选择性衰落就是在不同频率上的衰落不同。
什么是平坦衰落？如何区别平坦衰落和频率选择性衰落？
如果在信号的整个带宽上的衰落相差不大，称为平坦衰落。判断是平坦衰落还是频率选择性衰落，不仅仅取决于信道，还取决于信道和信号带宽之间的关系。若信号带宽小于信道的相干时间，就是平坦衰落；若信号的带宽远远大于信道的相干时间，就是频率选择性衰落。
需要注意的是：信道的时间选择性是由多普勒频移引起的，频率选择性是由时延扩展引起的。
3、信道衰落的影响
信道引起的衰落产生两个方面的影响，一是降低了信号的强度，使得信号跟容易被噪声污染；二是多路径的作用使信号产生扭曲，从而引起符号间干扰。

今天的文章多径信道会引起什么现象_最大信道利用率公式分享到此就结束了，感谢您的阅读。