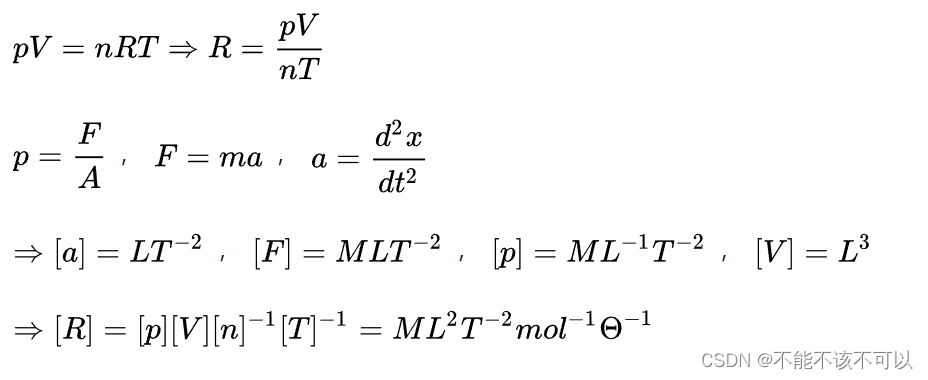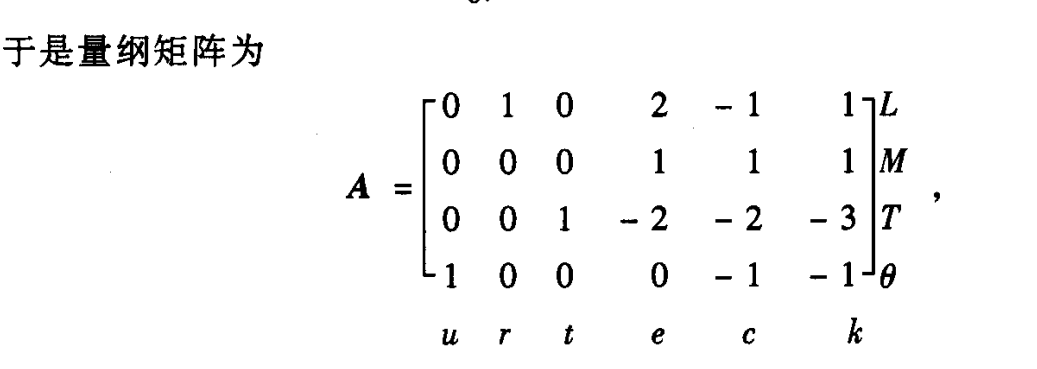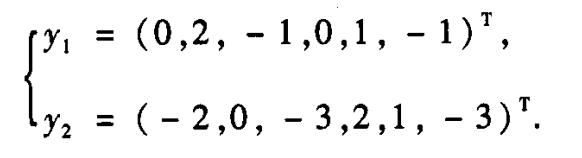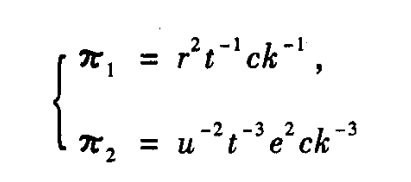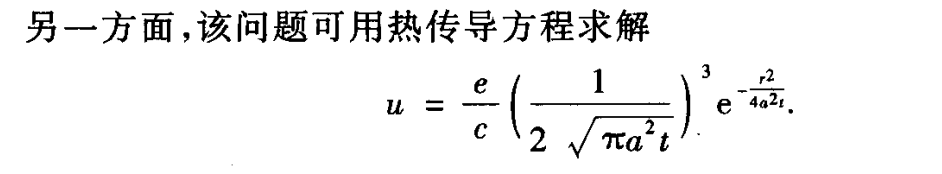2.1 量纲分析方法
换个角度思考,根据量纲我们是否能得到有关未知物理公式的有用结论?量纲分析方法就是为此而生
2.1.1 量纲
定量描述一个物理概念总离不开其特性,比如时间、质量、密度、力等,这些表示不同物理特性的量,称之为具有不同的“量纲”,记为【 · 】.当用数学公式描述一物理量时,等号的两端就必须保持量纲的一致性和单位的一致性。
2.1.2 量纲齐次原则
定理(Buckingham Pi) 设有

矩阵



心得:这段话写的非常绕,简而言之,就是调整相关量q的指数能够得到无量纲数(我们可以设为
2.1.3 量纲分析的一般步骤和例子
- 列出所有可能涉及到的物理量并找出他们的量纲
- 使用Buckingham’s PI Theorem找出不相关无量纲物理量的组
- 利用各个不相关无量纲物理量的组是无量纲的特点 ,去得到各个物理量之间的指数关系
例子:空间点热源的扩散问题
设初始时刻t=0在空间中有一热量为e的瞬时热源位于原点处(r=0),热量通过介质想无穷空间扩散,介质的初始温度为0,试从量纲角度研究点热源的扩散规律。
分析:设u=u(r,t,e,c,k),c是介质的比热容,k是介质的扩散系数由物理公式
现在我们分析一下各物理量的量纲
解线性方程组AY=0可得
这样我们就得到了两个相互独立的无量纲的量
注意,这里的函数g是未知的,有时候我们要依靠实验数据进行模拟检验推测函数g
今天的文章量纲分析法建模的优缺点_用量纲分析方法给出速度v的表达式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/85117.html