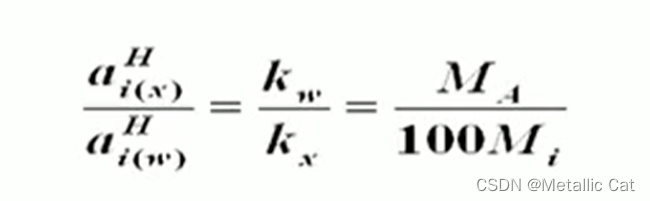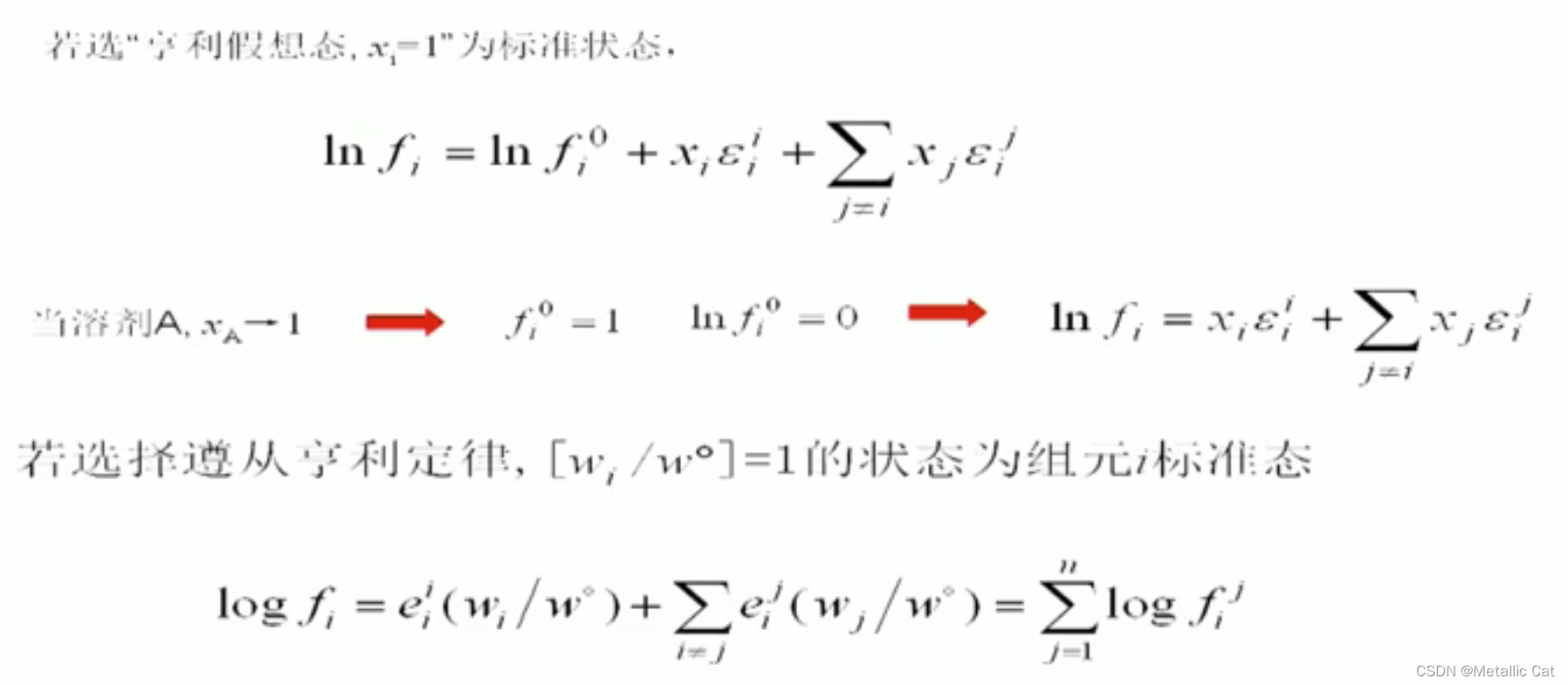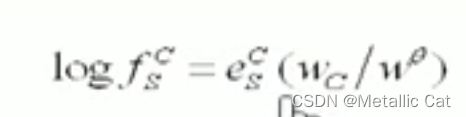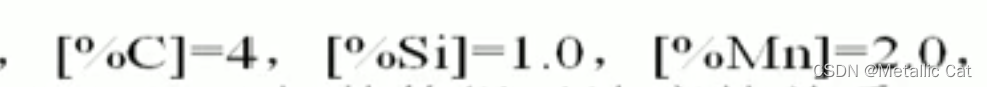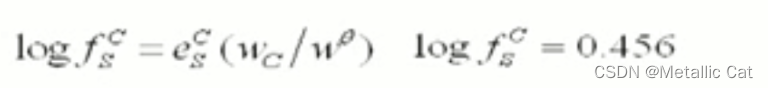物理化学复习【2】– 活度标准态转换与活度相互作用系数

第一部分 — 活度标准态转换

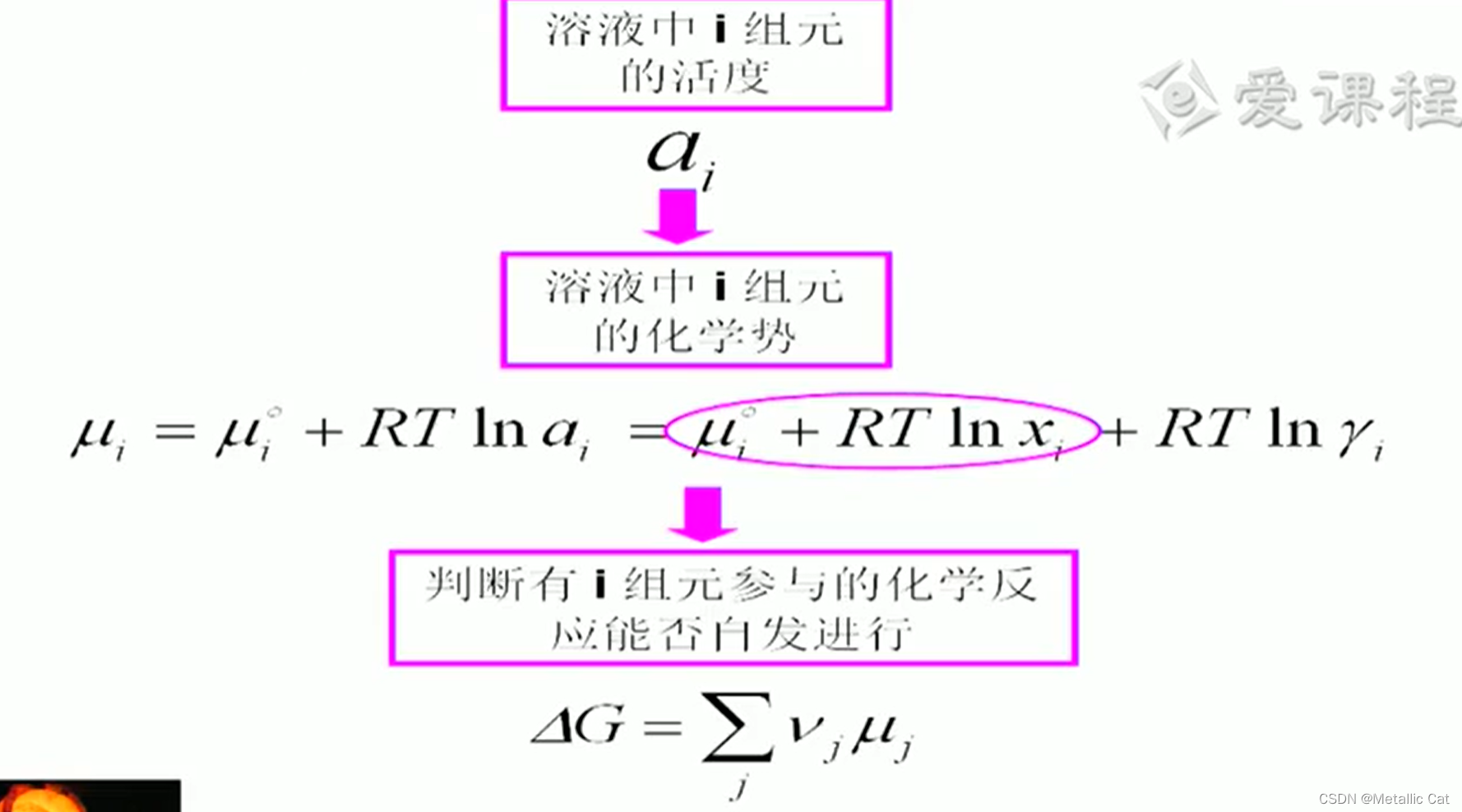
这里面被圈中的部分是溶液为理想溶液时计算得到的化学势，后面那一部分则是对理想溶液下计算得到的化学势进行的修正

吉布斯自由能变等于 = 反应物和生成物的自由能之和，其中在求和之前必须给每一个生成物/反应物乘上其对应的化学计量数，并且反应物的化学计量数都得在加上负号之后再用来乘和求和。

对了这个化学计量数的符号表示就是上面那个  Vj

接下来开始讲不同标准态下的活度之间的换算 

aR是符合拉乌尔定律下的活度，aH是符合亨利定律下的活度 

 当溶液无限稀的时候，溶液符合亨利定律，所以此时亨利定律的修正系数就变为了1（已经符合定律 ，处于不用修正的状态）

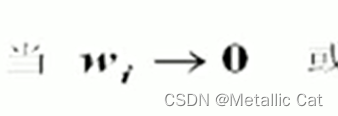
xi趋于0的时候，溶质无限稀，符合亨利定律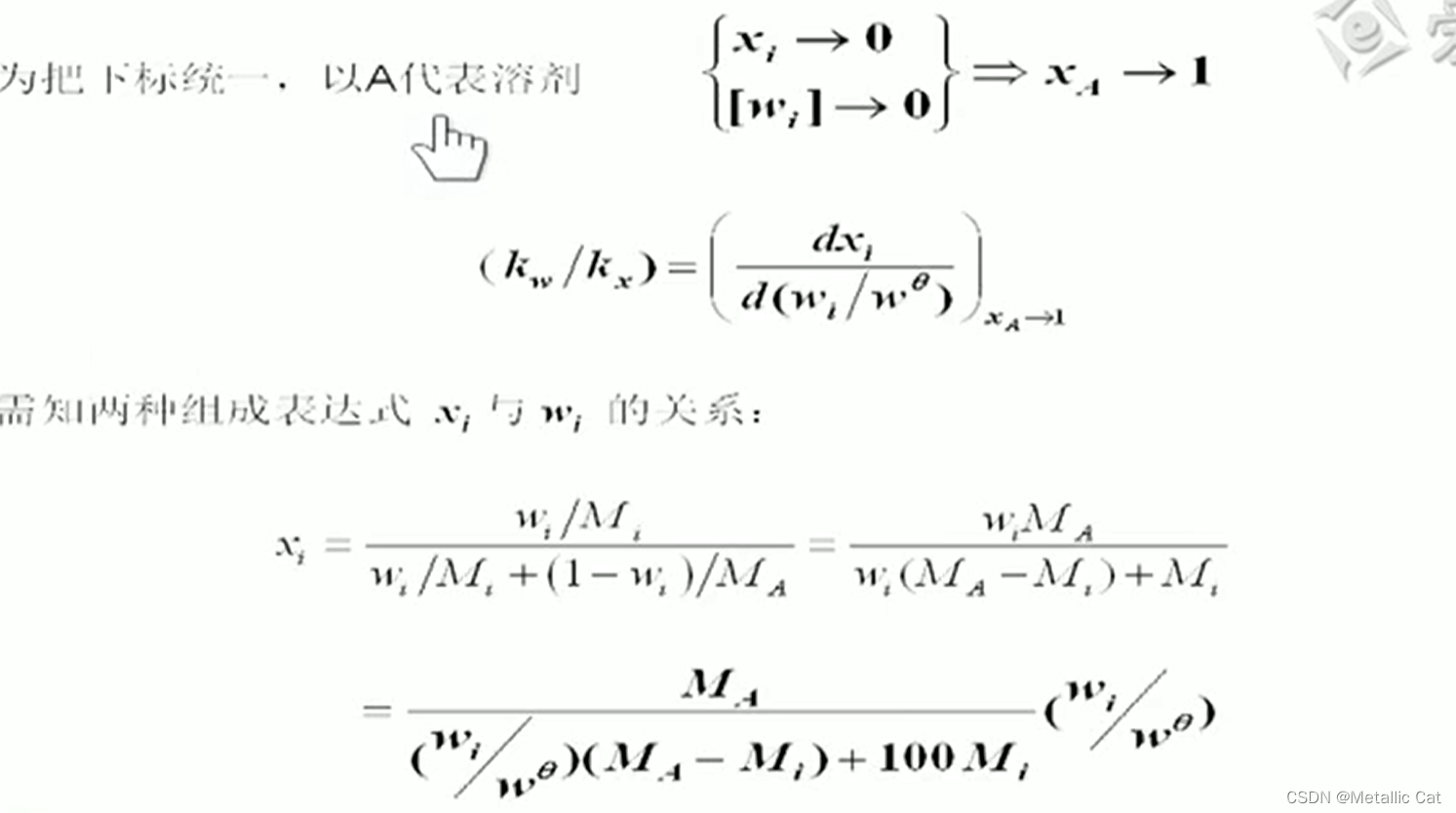 上面这个关系是通过设总质量为x求得的，总质量在代入公式后就已经被约掉了

 经过一系列变换之后就得到了xi与wi之间的关系

 wΘ 等于 1/100

kw和kx都是常数，无论是在哪个浓度组成下求得它们的比值，其它所有浓度组成下的这两个的比值就都知道了，所以我们通过求溶质浓度趋于0时的这两的比值，进而求得所有情况下的比值

 A是溶剂

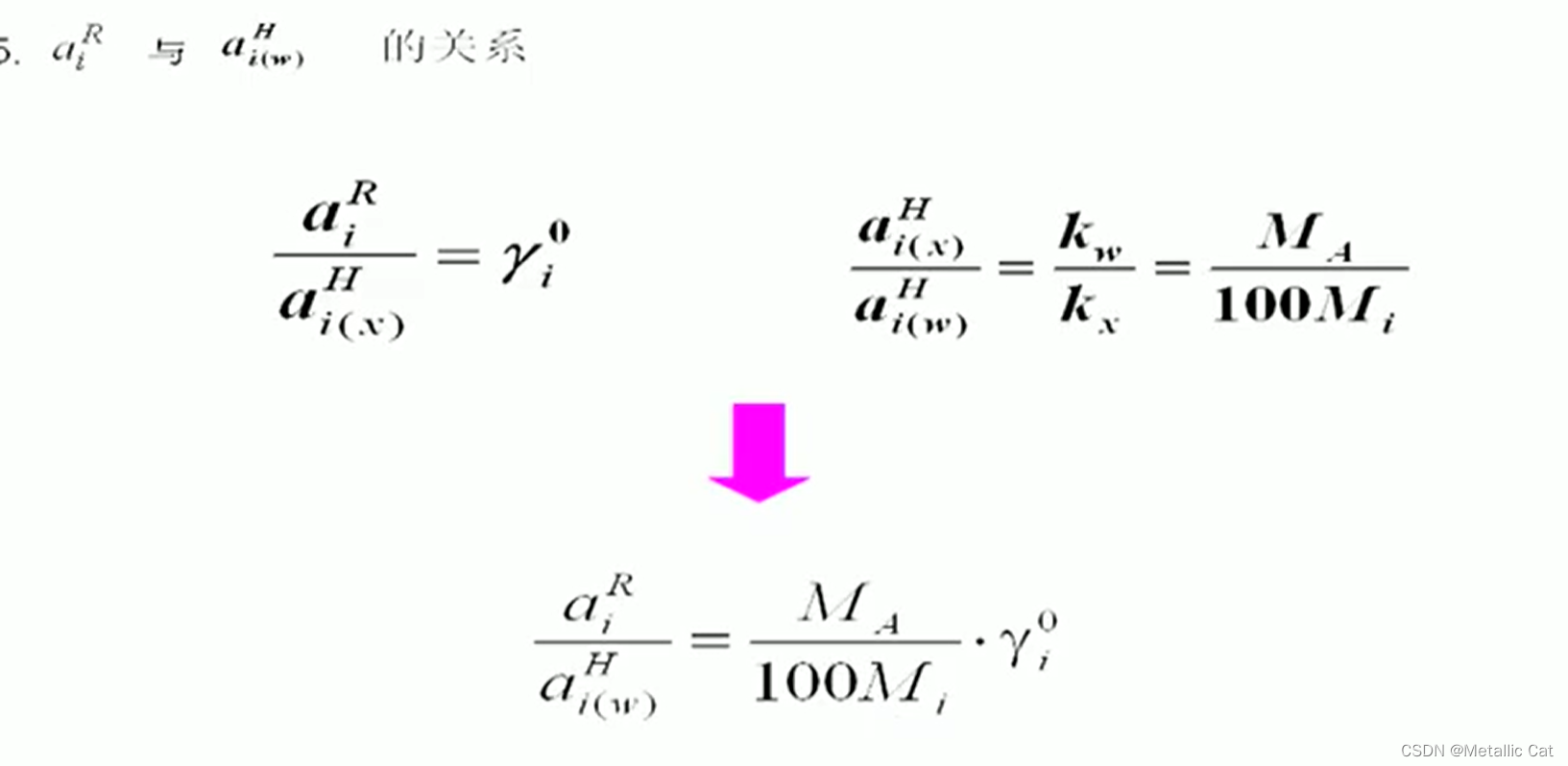
已知活度之间的关系的话，我们就可以开始求活度系数之间的关系(满足亨利定律的前提下)

当wi趋于0的时候，溶液同时符合质量浓度下的亨利定律与摩尔浓度下的亨利定律，所以不需要修正，所以此时两种标准态下的修正系数都等于 1 

 γi0是活度之比的结果，它等于 γi / fi

综上我们就有了aiR ,aiH和aiW之间的关系 

 第一个是“故仅涉及活度系数”

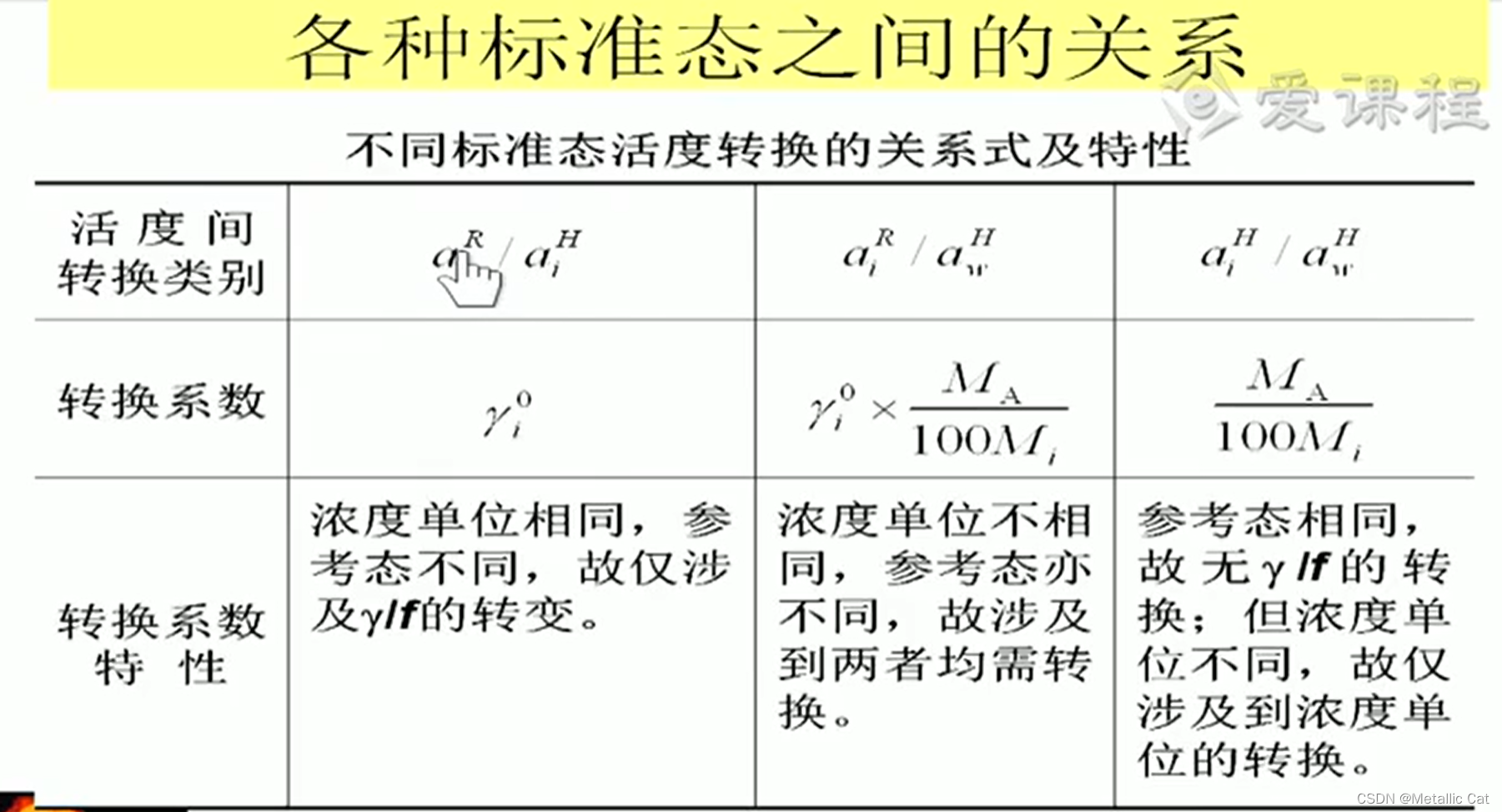
标准态之间的转换涉及到两种状况：

1.浓度单位不一致（摩尔浓度，质量浓度）

2.对应的定律不一致 — 标准态不一致 （亨利和拉乌尔）

将不同的转换为相同的就完成了转换了

活度与温度和压力之间的关系

 组成xi与温度无关，所以组成xi与温度的偏导等于0，而活度系数则是一个与温度相关的量

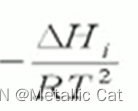
 上面这个为正值的时候，活度与温度成正比，反之成反比

如果吊塔Hi等于0的话，温度对活度没有影响

 可以认为活度/ 活度系数与压力无关 

第二部分 — 活度相互作用系数

以拉乌尔定律为依据的时候的活度相互作用系数

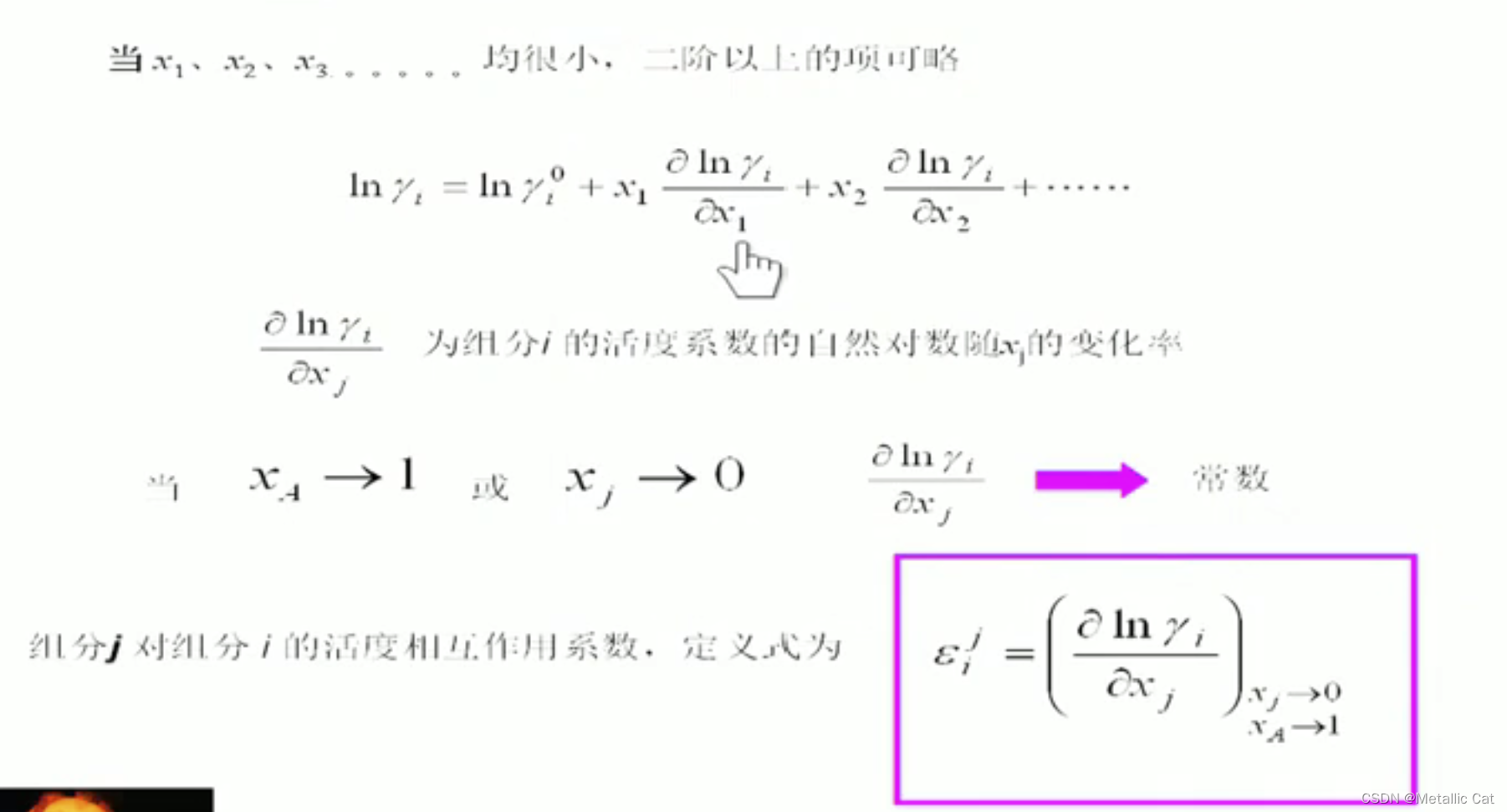
 在多组分系统当中，i 组元的活度系数是和溶液的组成相关，所以在恒温恒压的条件下，我们有上图中那样的关于活度系数 ln值 的公式

γi0表示的是除xi组元以外的组元都消失的时候，组元 i 的活度系数

由于xi趋于0，所以说二阶以上的展开项可以直接忽略掉，只留一阶展开项 

 对A – i 二元系的意思是溶是A，溶质是 i 的一个二元系

从只能描述无限稀溶液拓宽到能够描述极稀溶液，这个极稀溶液仍然要保证（摩尔浓度与分压保持线性关系） 

以亨利定律为依据来求活度相互作用系数

 上面这个最后一个公式的意思是，i组元的活度系数的Log值等于所有i组元在每一个组元影响下的活度系数的log值之和

如下面这个图求的就是碳的浓度对s的活度系数的贡献

 上面两个分别是拉乌尔定律下的活度相互作用系数(选用摩尔浓度）和亨利定律下的活度(选用质量浓度)相互作用系数（包括自身相互作用系数） 

这里面符号的意思是【%X】= a x元素在溶液中所占的质量分数为百分之a 

例题如上：

上面这题中由于c的质量分数较大，已经不再极稀溶液的队列当中了，所以说不能用极稀溶液状态下的线性计算来求其对s的活度系数的贡献了，即：

这个是被否决的，我们应该直接选择查表或者题目给的c对s的活度系数的贡献，即左边这个：

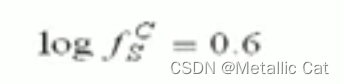
ps : 10的log（fs）次方就等于 fs

一定要在极稀溶液的条件下，使用活度相互作用系数来计算活度

今天的文章物理化学复习【2】– 活度标准态转换与活度相互作用系数分享到此就结束了，感谢您的阅读。