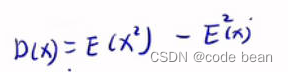期望均值方差是什么关系_期望和均值有什么区别「建议收藏」

前言

开始会给出公式，后面结合正态分布的的期望和方差，来更具体的理解他们。

期望

首先，期望全名“数学期望”，又名均值或估计值，注意和平均值不是一个概念。这个后续再说。

说到期望，就得先说分布列。

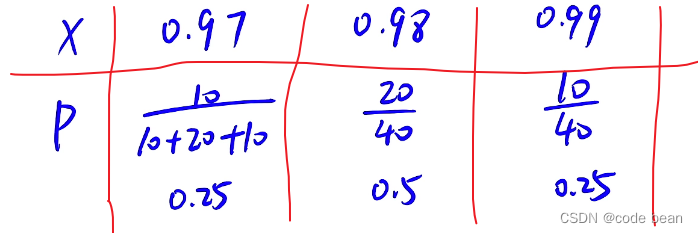
X 表示不同种类的事件对应的数值，P表示每钟事件发现的概率 。

什么叫做事件对应的数值，这其实是我们自己下的一个定义，比如抛正面得1分。

再比如：

 这里得到得分布列应该是：

 那么有了分布列，就可以求期望了，或者说求均值/估计值。这里用EX表示期望：

 哪有了分布列，求期望和非常简单的。(如上图：相乘再相加)。这里也看出了它与平均值的不同，平均值是将已经发生的情况进行统计，求平均。期望是已知概率的分布，估计一个最可能出现的值。

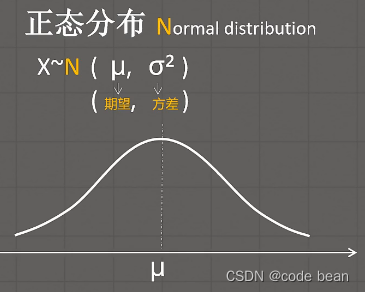
那为了，进一步理解期望，这里引入，上帝规则——正态分布：

 这里我们就可以看到，期望EX和X轴是挂钩的，再正态分布中，当X等于期望时，此时对应的Y值最大，但是这里要注意，正态分布中，Y值并不是X对应的概率值，正态分布不是概率的曲线，而是概率的密度曲线，这里说下我的理解（不一定对）：假设X是可以无限细分的，这个曲线是一个身高的正太分布，假设一个人的身高是1.60025499尽无限细分，另外一个人的身高是2.045648842无限细分。那这两个身高，谁的概率高？他们都无限接近0. 但是如果说的是一个范围，比如身高在1.65米左右的和身高在2.2米左右的，谁的概率高，那很显然是前者。

这里曲线的下方面积才是概率P。曲线下方总面积面积为1.

这个图形对应的是概率密度函数f(X)，所以Y值对应的是累计分布函数F(X)的一阶导数，即F(X)的瞬时变化率。实际意义就是那个X对应的密度值。也就是概率累积最快的地方。

所以这里，我们发现Y值其实个很抽象的，就是我知道的X但是我得到一个Y，但是这个Y对于我来说意义不大，我之知道此时Y最大。所以往往我们是反过来看的！我们知道了最大的Y，然后看对应的X是多少，而X的含义是具体的。比如Y最大时X=1.6，那1.6就是期望就是均值。而样本确定的情况下，均值和平均值时相等的。

课参考参考：

​​​​​​均值与期望到底是不是一回事？ – 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/311896697说到这里，关于期望的部分就解释完了。

那什么时方差？

首先给出公式

 从公式看，方差和期望还有概率时相关的，（期望本身和概率也是相关的）。方差描述的时一组数据（样本）的离散程度。

 这里可以结合偏差，来对比理解下方差。

那通过化简公式，我们最终得到公式，其中D(x)表示方差：

 化简过程如下：

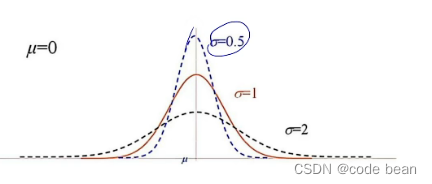
 这里我同样引入正态分布，进一步理解方差。

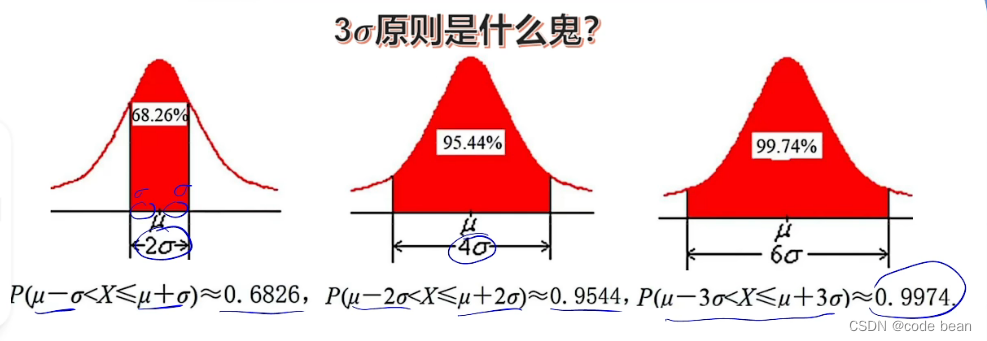
当西格玛确定下来之后，还有个一个3西格玛原则，可以看看：（这里其实还有个标准差的概念，就是这个西格玛，西格玛的平方就是方差）

  这里都可以看出当方差越大时，在相同的区域内，面积越小，即概率越小，这说明数据越分散。

小结： 

        1 那在深度学习中，这种方差大模型可能需要更多的分类才能更好的界定。

        2 方差和期望和概率是强相关的，每种事件对应的值都需要乘上概率P，在做其他计算。

参考资料：

​​​​​​【#11】【28天战胜高考数学】分布列 数学期望 方差 | 高中数学 | 高考数学_哔哩哔哩_bilibili

【概率·正态分布】这是个啥玩意儿？10分钟完全入门！_哔哩哔哩_bilibili

跟李沐学AI的个人空间_哔哩哔哩_bilibili

今天的文章期望均值方差是什么关系_期望和均值有什么区别「建议收藏」分享到此就结束了，感谢您的阅读。