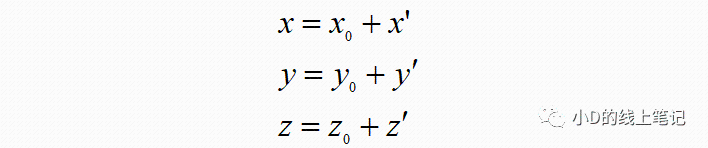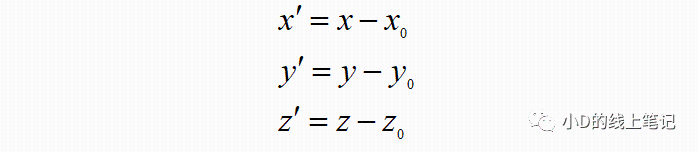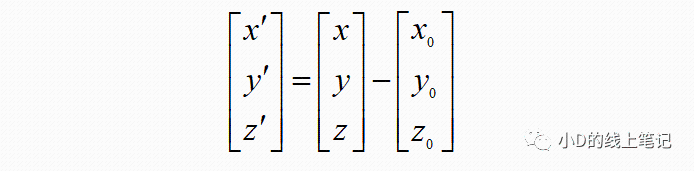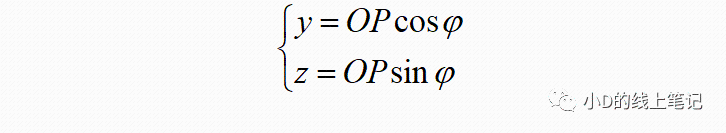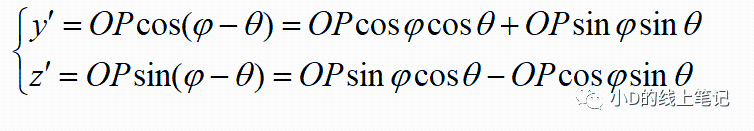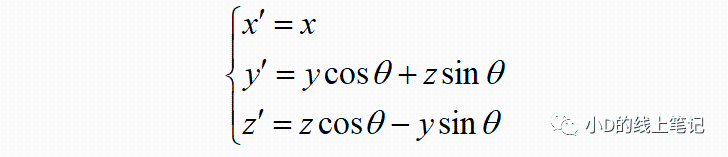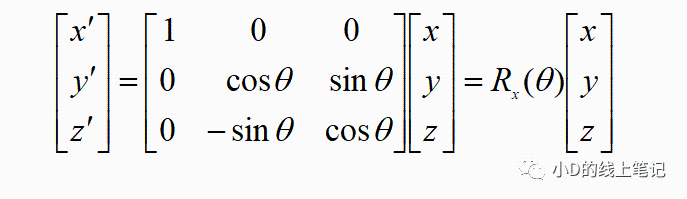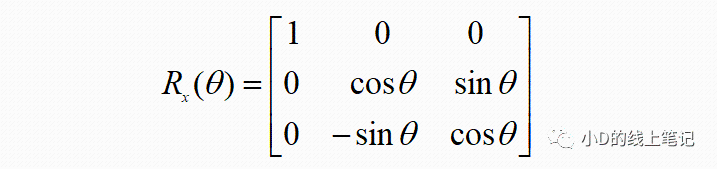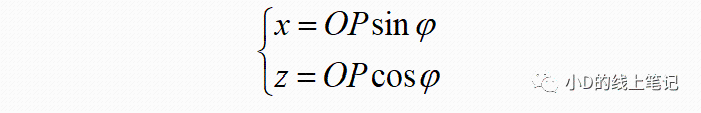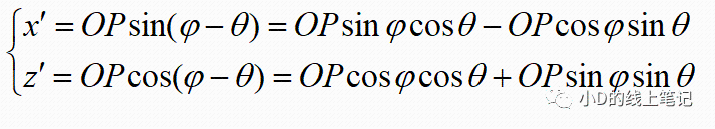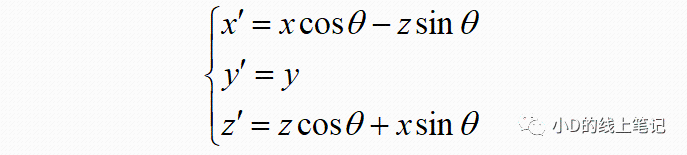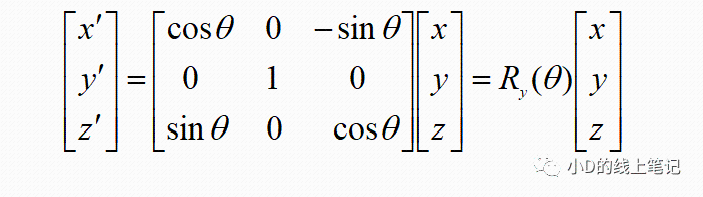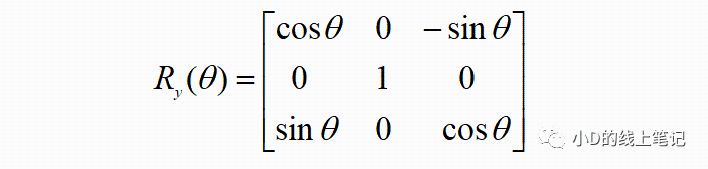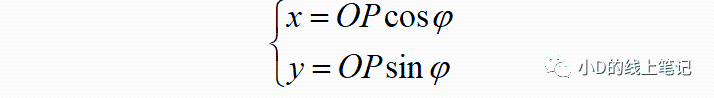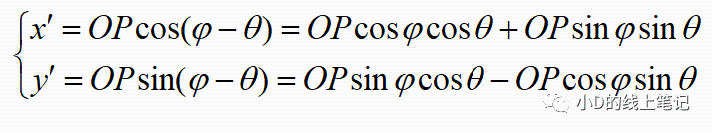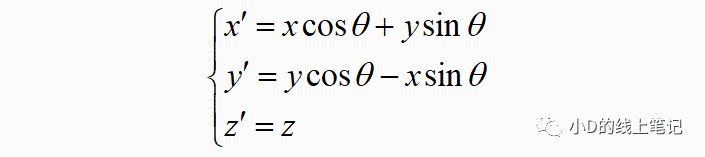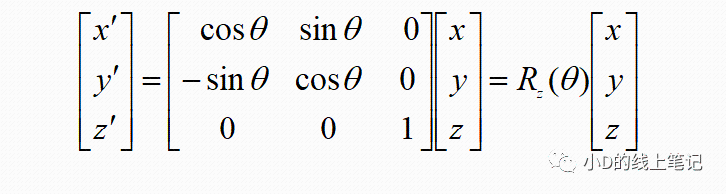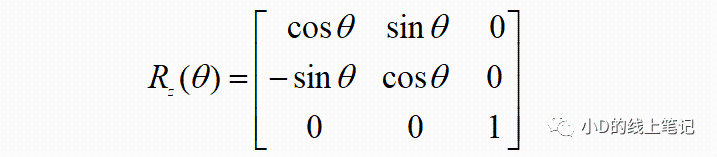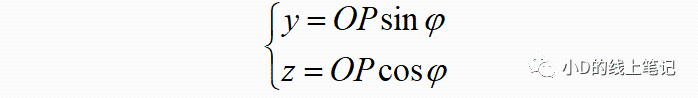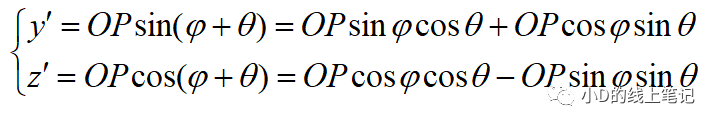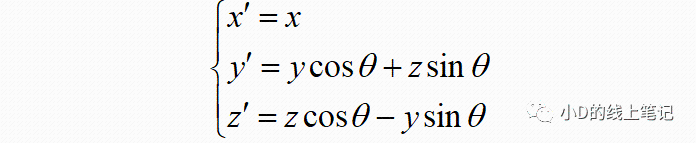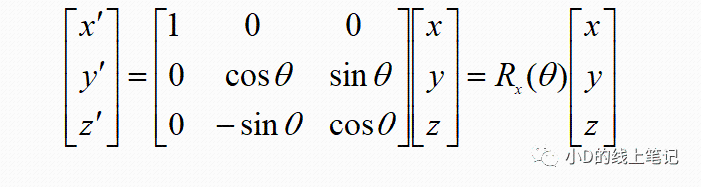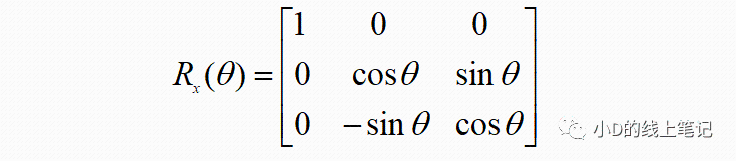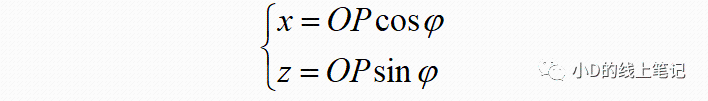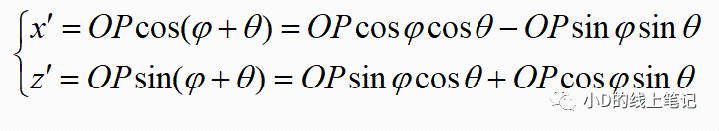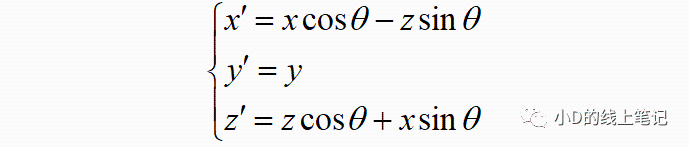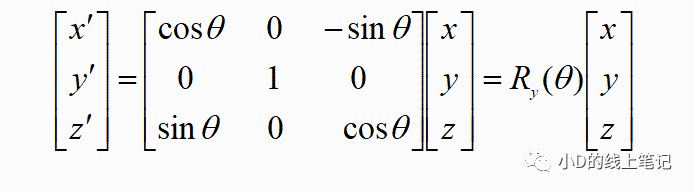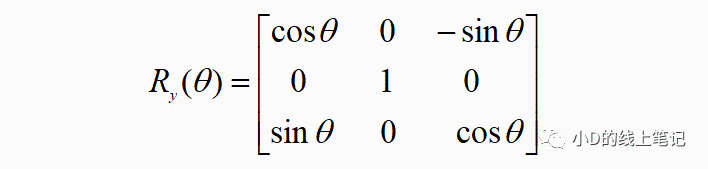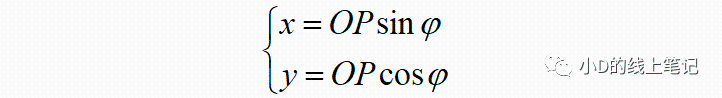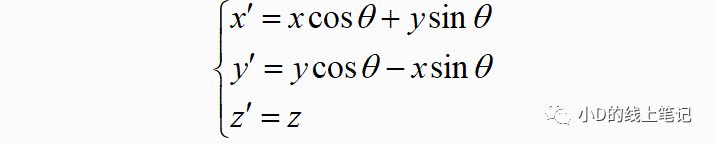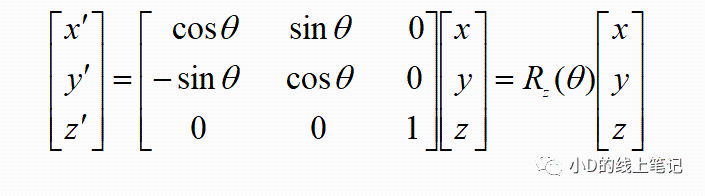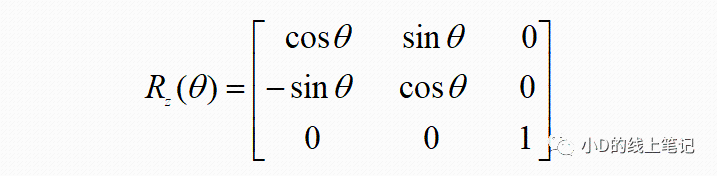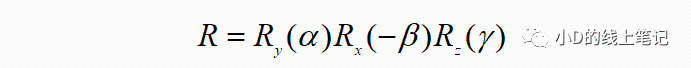坐标系平移旋转变换公式_求两个坐标系的转换矩阵

这次的文章，我们来看一看三维空间直角坐标系的平移和旋转变换，尽管这个内容早已见诸文献资料，但自己在看书籍以及期刊论文时，总是遇到让人百思不得其解的事情，就是不同的文献给出的同类型的旋转矩阵居然有不一样的，这让小D对文献中的公式产生了怀疑，也不知道哪个旋转矩阵才是对的。

于是，自己动手，丰衣足食，为了验证公式的正确性，小D把旋转矩阵推了个遍，包括文献中只给出了公式而没有过程的旋转矩阵的推导。

三维空间直角坐标系的平移变换

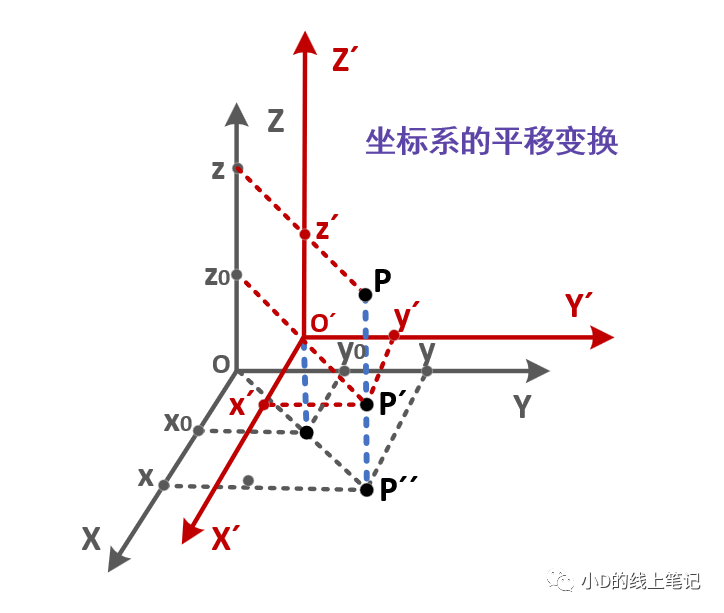
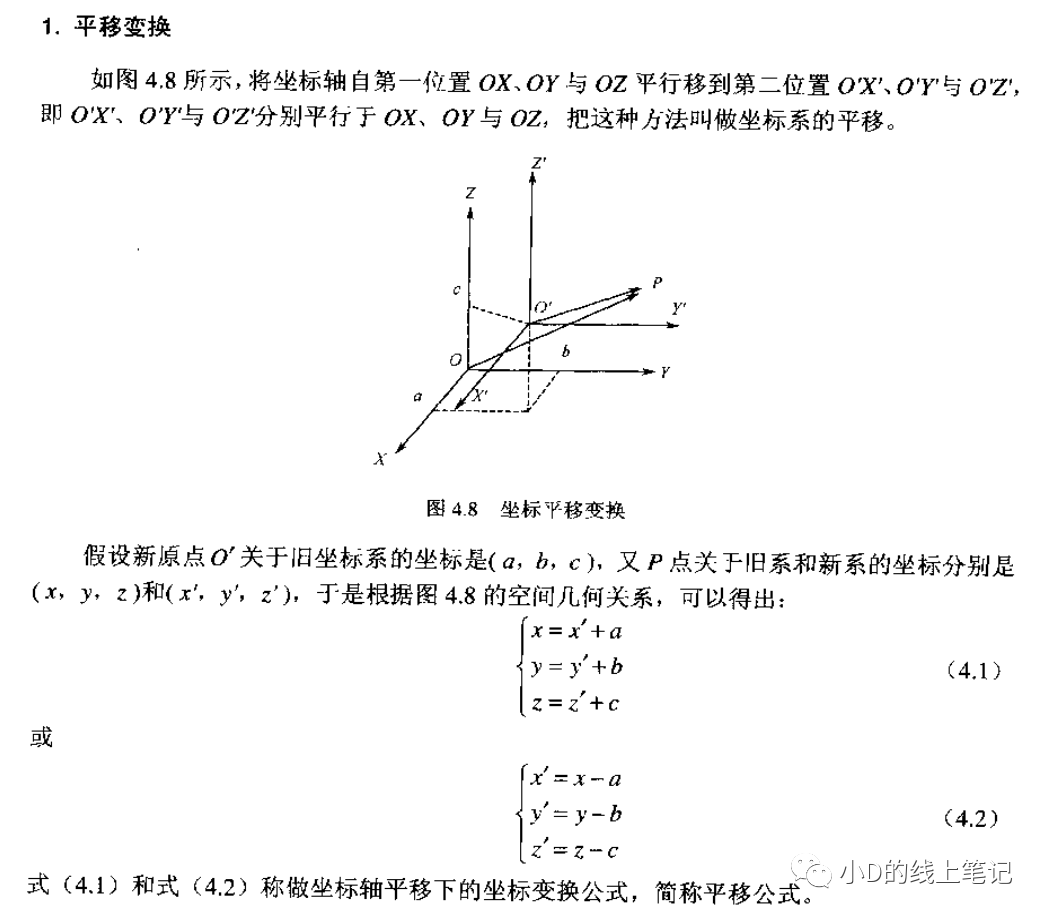
文章的开头，还是先讲讲坐标系的平移变换，平移变换的过程如下图所示：

假设点P是空间中的任意一点，其在XYZ坐标系中的坐标为(x, y, z)。现在点P不动，我们将XYZ坐标系做一个平移的操作，把XYZ平移到X´Y´Z´的位置，O´是平移后的坐标的原点，要注意的是，O´在XYZ中的坐标为(x0, y0, z0)。点P在XYZ坐标系中的坐标为(x, y, z)，点P在平移后的坐标系X´Y´Z´中的坐标为(x´, y´, z´)。根据上面这个示意图，聪明的你一下就可以发现：

通过上面的式子，我们可以求解出点P在X´Y´Z´坐标系中的坐标为：

把上面的式子转换成矩阵的形式就是：

这就是三维空间直角坐标系的平移变换了。

三维空间直角坐标系的旋转变换

下面我们来看看三维空间直角坐标系的旋转变换，小D最开始在研究旋转变换的时候，只推导了右手坐标系的旋转变换。有一次看到了一篇文献，它用的是左手坐标系，但小D对文献中给出的公式的正确性感到怀疑，而我们要在代码中用到相关的坐标转换，这意味着我们需要知道左手坐标系旋转矩阵的正确表达式，所以小D又把左手坐标系的旋转矩阵推导了一遍。

右手坐标系的旋转变换

右手坐标系的旋转过程有三个，分别是绕X,Y,Z轴旋转，右手坐标系在旋转时，通常规定以逆时针旋转方向为正方向。

①XYZ右手坐标系绕X轴逆时针旋转θ角

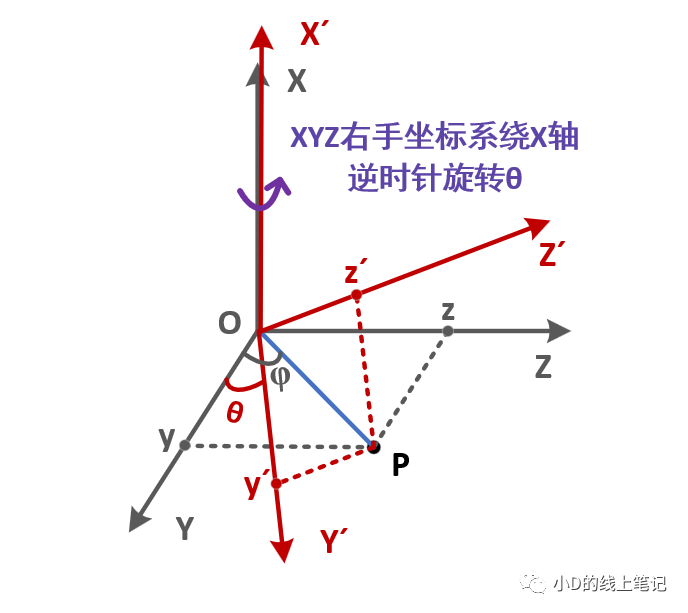
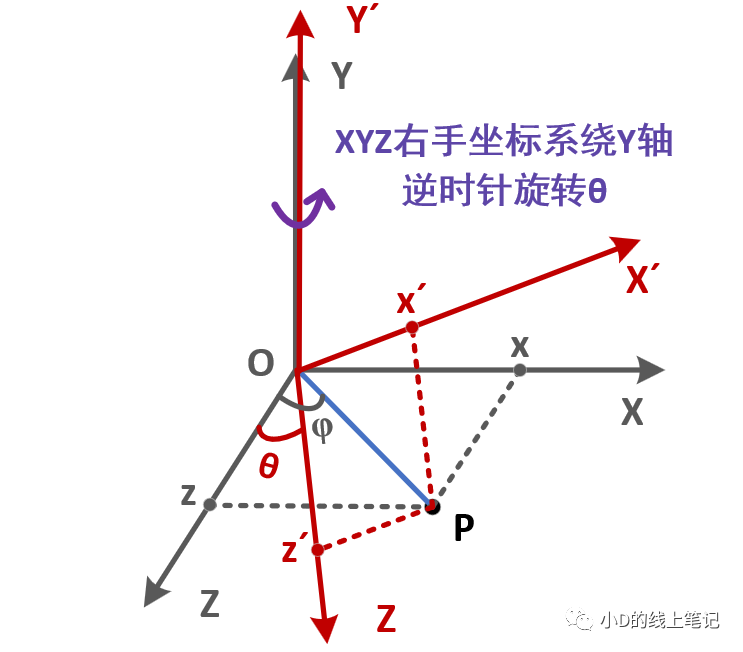
先来推导右手坐标系绕X轴旋转的旋转矩阵，这个过程可以用下面这个示意图表示：

假设P点为空间中任意一点，为了便于观察与推导，我们将P点放在YOZ平面内。P点在空间中保持不动，XYZ坐标系绕X轴逆时针旋转θ形成新的坐标系X´Y´Z´，P点在XYZ中的坐标为(x, y, z)，P点在X´Y´Z´中的坐标为(x´, y´, z´)，现在我们已知(x, y, z)、旋转角度θ和(x´, y´, z´)，求旋转矩阵Rx。在推导的过程中，我们还要假设一个变量，就是点P相对于Y轴正方向逆时针的夹角为φ。

很明显，点P在XYZ坐标系中的Y,Z轴坐标可以表示为：

点P在X´Y´Z´坐标系中Y´,Z´轴坐标为：

把x，y带入x´，y´中，同时P点在XYZ中X轴坐标与其在X´Y´Z´坐标系中的X´轴坐标是相等的，所以有：

把这个表达式表示成矩阵相乘的形式为：

上面的Rx就是XYZ右手坐标系绕X轴逆时针旋转θ角，空间中的点从XYZ坐标系变换到X´Y´Z´坐标系的旋转矩阵，Rx的表达式为：

②XYZ右手坐标系绕Y轴逆时针旋转θ角

有了前面的推导过程，XYZ右手坐标系绕Y轴逆时针旋转θ角的旋转矩阵的推导就一葫芦画瓢了。旋转过程如下图所示：

点P在XYZ右手坐标系中的X,Z轴坐标为：

点P在X´Y´Z´坐标系中的X,Z轴坐标为：

把x，z带入x´，z´中，同时P点在XYZ中的Y轴坐标与X´Y´Z´坐标系中的Y´轴坐标是相等的，所以有：

写成矩阵相乘的形式：

所以，XYZ右手坐标系绕Y轴逆时针旋转θ角的旋转矩阵Ry为：

③XYZ右手坐标系绕Z轴逆时针旋转θ角

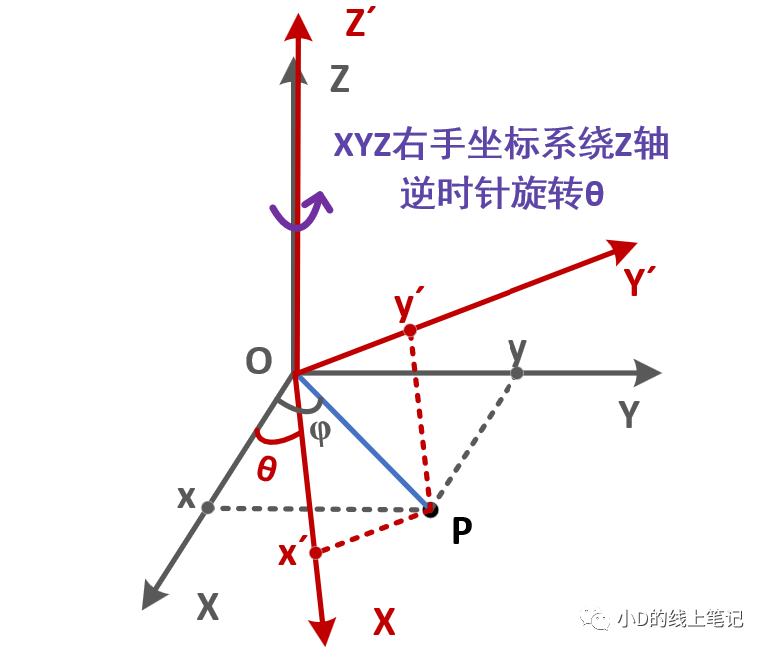
XYZ右手坐标系绕Z轴逆时针旋转θ的过程如下图所示：

点P在XYZ右手坐标系中的X,Y轴坐标为：

点P在X´Y´Z´坐标系中的x,y坐标为：

把x，y带入x´，y´中，同时P点在XYZ中的Z轴坐标与其在X´Y´Z´坐标系中的Z´轴坐标是相等的，所以有：

写成矩阵相乘的形式：

所以，XYZ右手坐标系绕Z轴逆时针旋转θ角的旋转矩阵Rz为：

左手坐标系的旋转变换

左手坐标系的旋转过程也是三个，分别是绕X,Y,Z轴旋转，左手坐标系在旋转时，通常规定以顺时针旋转方向为正方向。

①XYZ左手坐标系绕X轴顺时针旋转θ角

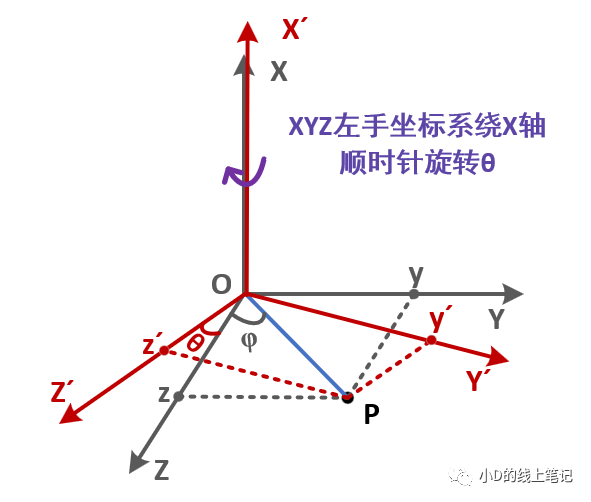
XYZ左手坐标系绕X轴顺时针旋转θ角的过程示意图如下所示：

上图中，点P为空间中任意一点，点P保持不动，XYZ左手坐标系绕X轴顺时针旋转θ角形成新的坐标系X´Y´Z´。已知点P在XYZ坐标系中的坐标为(x,y,z)，点P在X´Y´Z´中的坐标为(x´,y´,z´)，我们要求的是XYZ坐标系变换到X´Y´Z´坐标系这个过程中的旋转矩阵。

从图中可以看出，点P在XYZ坐标系中的Y,Z轴坐标为：

点P在X´Y´Z´坐标系中的Y,Z轴坐标为：

把y，z带入y´，z´中，同时P点在XYZ中的X轴坐标与其在X´Y´Z´中的X´轴坐标是相等的，所以有：

写成矩阵相乘的形式：

所以，XYZ左手坐标系绕X轴顺时针旋转θ角的旋转矩阵为：

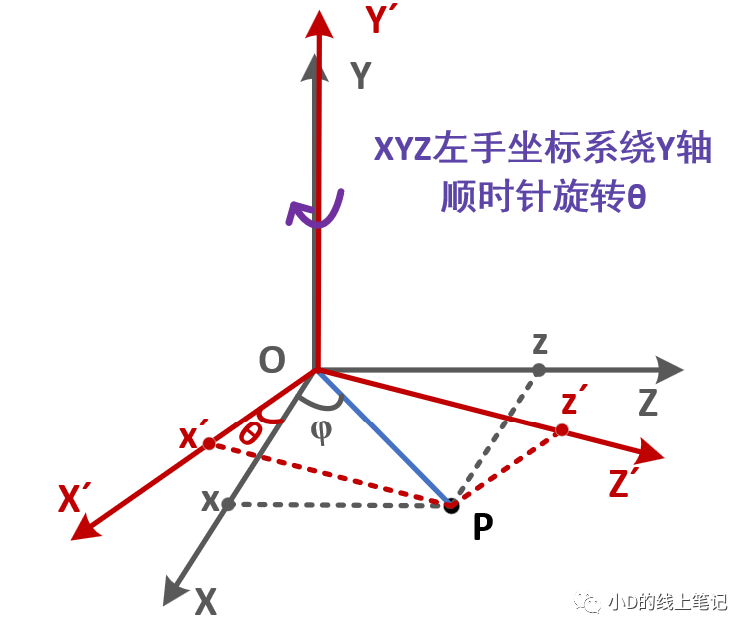
②XYZ左手坐标系绕Y轴顺时针旋转θ角

XYZ左手坐标系绕Y轴顺时针旋转θ角形成X´Y´Z´坐标系，其过程示意图如下所示：

点P在XYZ坐标系中的X,Z轴坐标为：

点P在X´Y´Z´坐标系中的X,Z轴坐标为：

把x，z带入x´，z´中，同时P点在XYZ中的Y轴坐标与其在X´Y´Z´坐标系中的Y´轴坐标是相等的，所以有：

以矩阵形式表示为：

所以，XYZ左手坐标系绕Y轴顺时针旋转θ角的旋转矩阵Ry为：

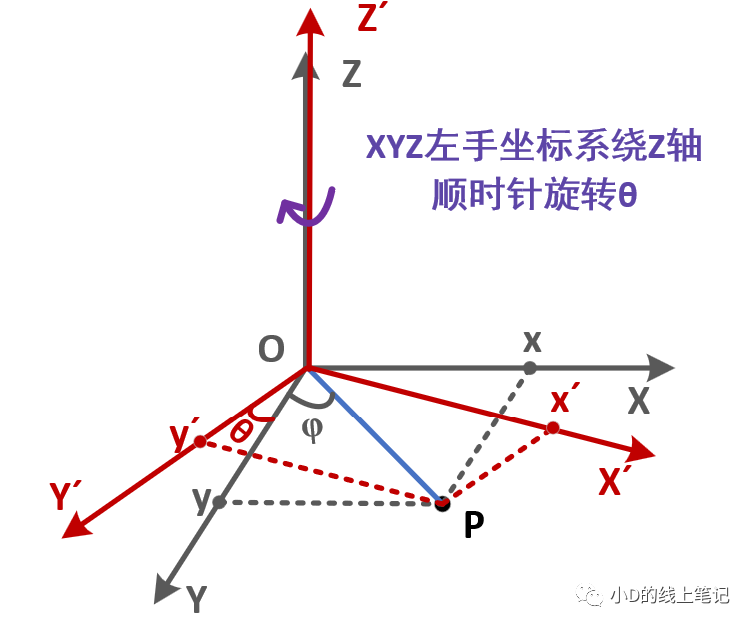
③XYZ左手坐标系绕Z轴顺时针旋转θ角

XYZ左手坐标系绕Z轴顺时针旋转θ角形成X´Y´Z´坐标系的过程示意图如下所示：

点P在XYZ坐标系中的X,Y轴坐标为：

点P在X´Y´Z´坐标系中的X,Y轴坐标为：

把x，y带入x´，y´中，同时P点在XYZ中的Z轴坐标与其在X´Y´Z´坐标系中的Z´轴坐标是相等的，所以有：

将上式表示成矩阵的形式为：

所以，XYZ左手坐标系绕Z轴顺时针旋转θ角的旋转矩阵Rz为：

左手坐标系的旋转矩阵到这里就推导完啦。

旋转矩阵的运用

实际中，当我们要推导两个不同的坐标系，比如地心地固坐标系和北东天、北东天坐标系和机体坐标系等坐标系之间的变换关系时，就要用到上面的旋转矩阵。一般的方法是，根据实际的旋转过程，按旋转的先后顺序计算旋转矩阵。

比如对于右手坐标系，如果有一个过程是先绕Y轴逆时针旋转α，再绕X轴顺时针旋转β，最后绕Z轴逆时针旋转γ，那么最终的旋转矩阵的表达就是：

在应用旋转矩阵的过程中，小D还总结了一个经验：不管是左手坐标系还是右手坐标系，假如绕X轴逆时针旋转θ角，相当于绕X轴顺时针旋转2π-θ角，同时也相当于绕X轴顺时针旋转-θ角。

旋转矩阵的验证

推导了这么多公式，那推导结果是否正确呢？我们可以从《雷达数据处理及应用》中找到相关内容：

从书中的截图中可以验证，自己推导的平移变换以及右手坐标系的旋转矩阵是没有问题的。但是左手坐标系的推导，小D至今没有找到相关文献，但小D相信肯定是有的。

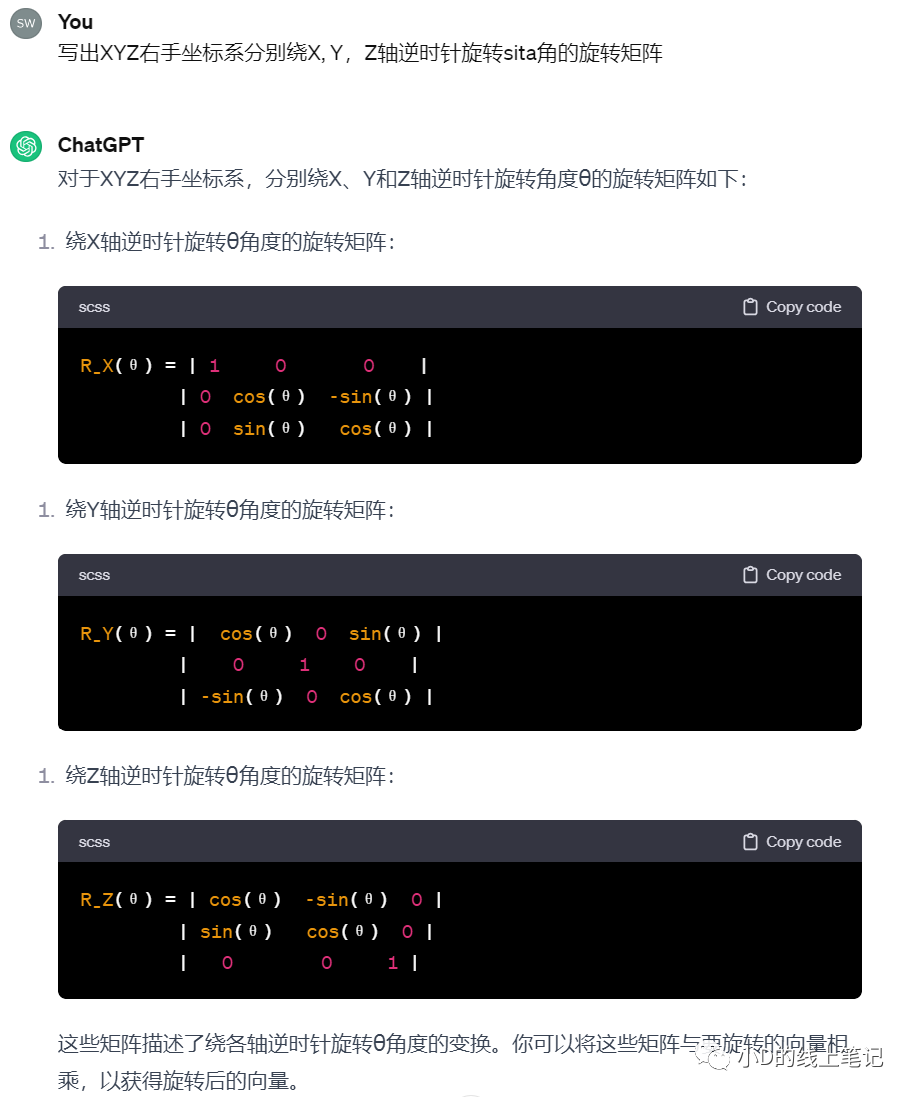
然后小D向gpt求证，gpt给出的答案是这样的：

很显然，gpt给出的右手坐标系的旋转矩阵不是小D上面推导的结果，也跟书中的结果不一样。于是小D又去问了gpt4，gpt4的回答是这样的：

gpt4的回答和gpt3.5的回答如出一辙，当时小D心想，gpt脑子估计又瓦特了。直到最近，小D看到了一本英文书籍Geometric Transformations for 3D Modeling_Michael Mortenson，小D才明白，原来gpt是没有正确理解问题，它给出的是坐标系中的点转动，坐标轴不动的情况。这本英文书籍中坐标转换相关的内容是这样的：