信息物理系统-Rijndael加密算法的实现:
概述:
AES标准的Rijndael算法是一种分组加密算法,本次实验通过PtolemyII软件,实现了明文长度为128位,密钥长度为128位的Rijndael加密算法。
实验的完成采取自底向上的,即先细分实现Rijndael算法的每个功能模块,通过一级一级地组合各个功能模块,从而实现整体的Rijndael加密算法;
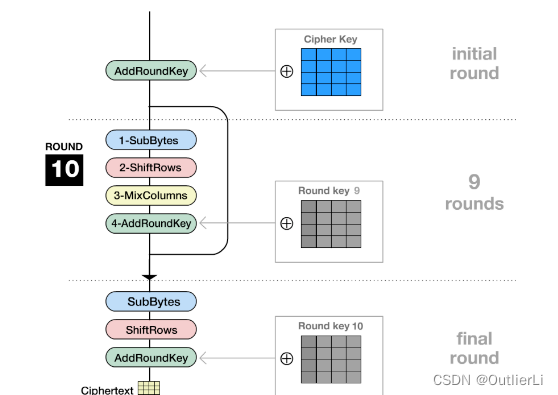
Rijndael加密算法的宏观流程:
很明显Rijndael被分成了三大块:第一块只有AddRoundKey(轮密钥加)一个子模块;第二块有四个子模块,分别是SubBytes(字节替换),ShiftRows(行移位),MixColumns(列混合),AddRoundKey(轮密钥加);第三块相比第二块,只少了一个列混合的子模块,所以我们完全可以把第二块的实现模块迁移到第三块。
各模块原理及PtolemyII实现:
一、输入:
原理分析:
输入分为明文输入和密钥输入,本实验实现的Rijndael算法的明文和密钥都是128bit,即16字节;每一个字节可以用2个十六进制数表示,如果将2个十六进制数分为一组,则需要16组;
考虑到PtolemyII中有较多的数组处理组件和函数,可以直接调用,使得后续步骤较容易实现;所以本实验采用一个有16个元素,每个元素为两个十六进制数的数组来保存128bit的信息;
具体实现:
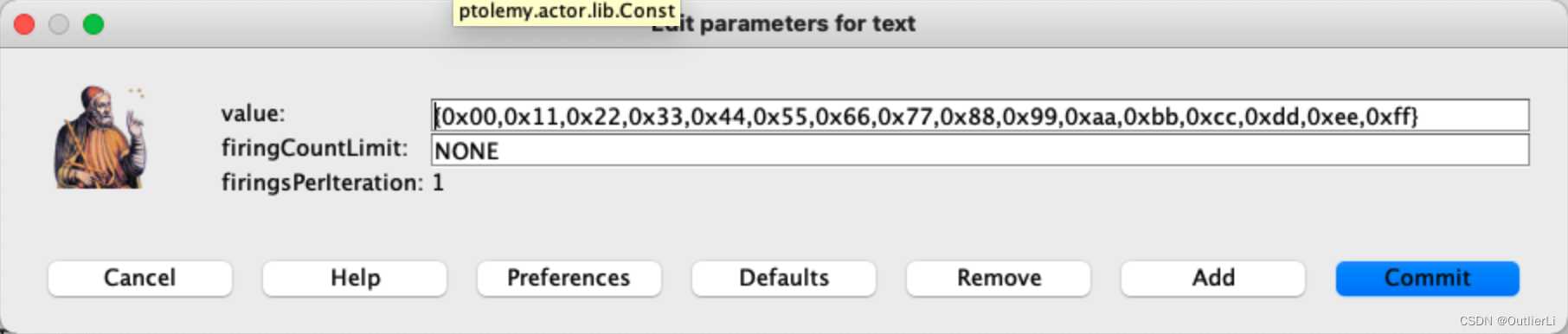
用const组件来保存数组常量,明文和密钥用两个const组件实现:
明文:
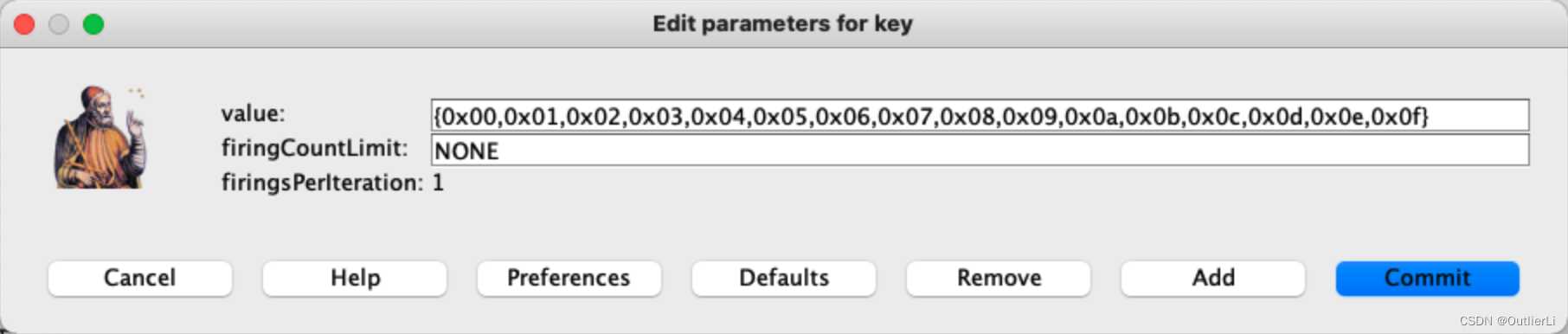
密钥:
二、轮密钥加(AddRoundKey):
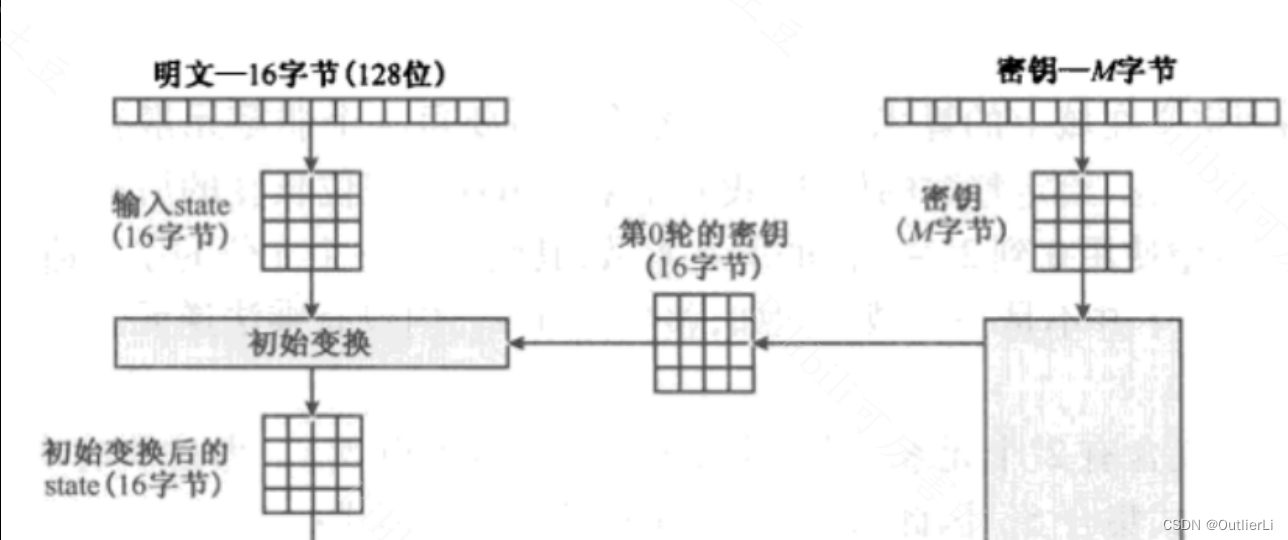
原理分析:
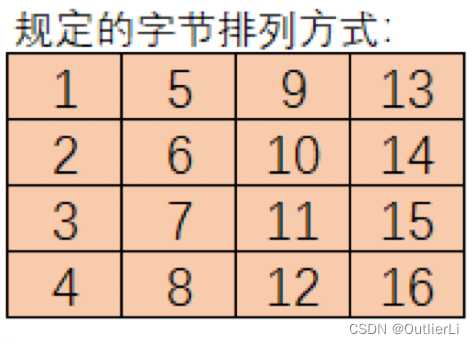
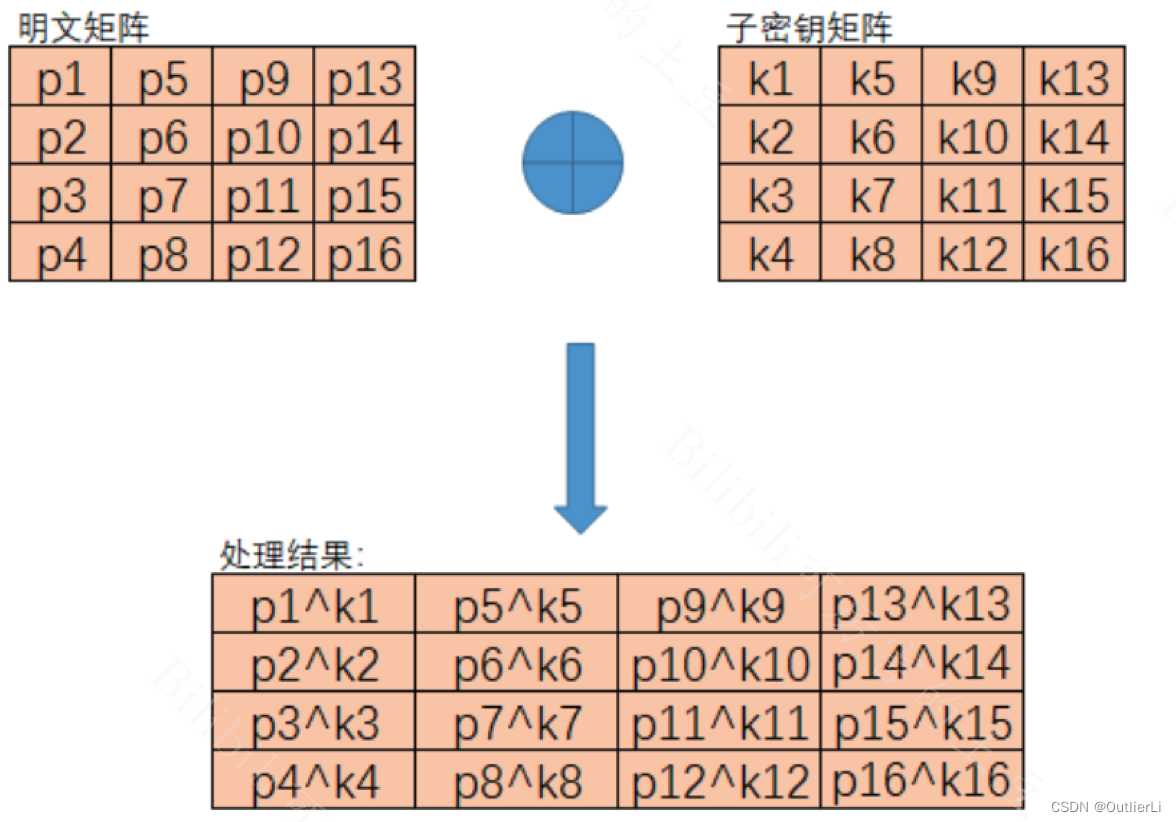
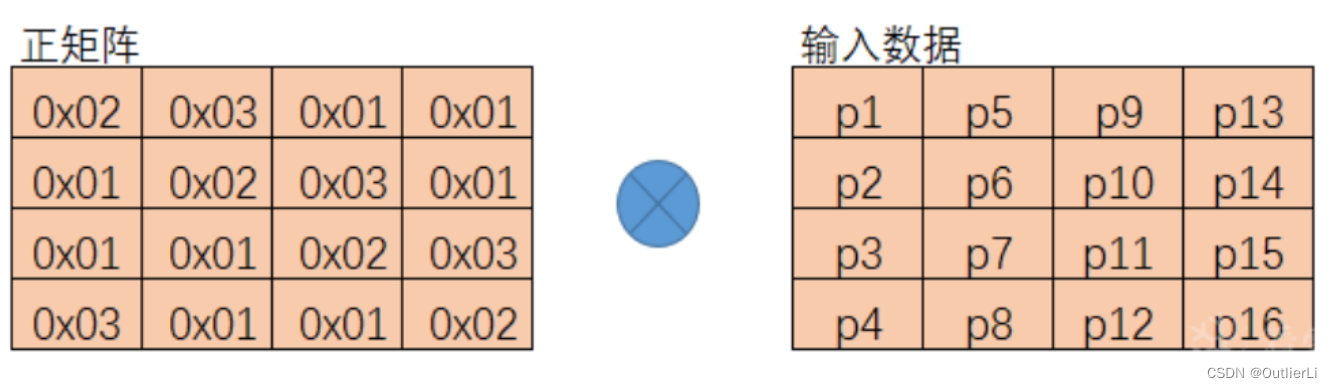
初始变换是将16字节的明文和16字节的密钥按照规定的字节排列方式(4*4矩阵),进行按字节异或;
矩阵的形式按字节异或和数组的形式按字节异或结果没有多大的区别,所以我们可以将矩阵异或转换成数组对应元素异或;
具体实现:
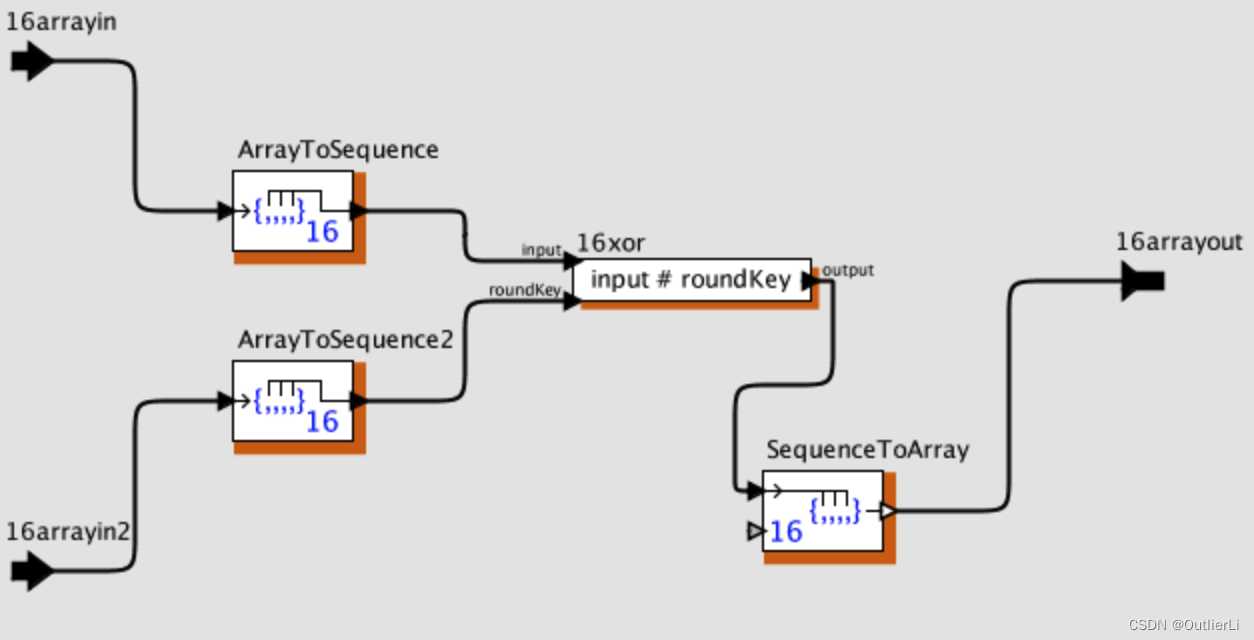
要实现在第一步中保存在两个const组件中的16个字节元素的数组的对应元素异或;就是要将数组中的元素都按顺序取出,然后按顺序异或,异或完成后再按顺序结合成一个数组,方便后续处理;
所以只需要:数组转序列,序列异或,异或后序列转数组;
三、字节替换(SubBytes):
原理分析:
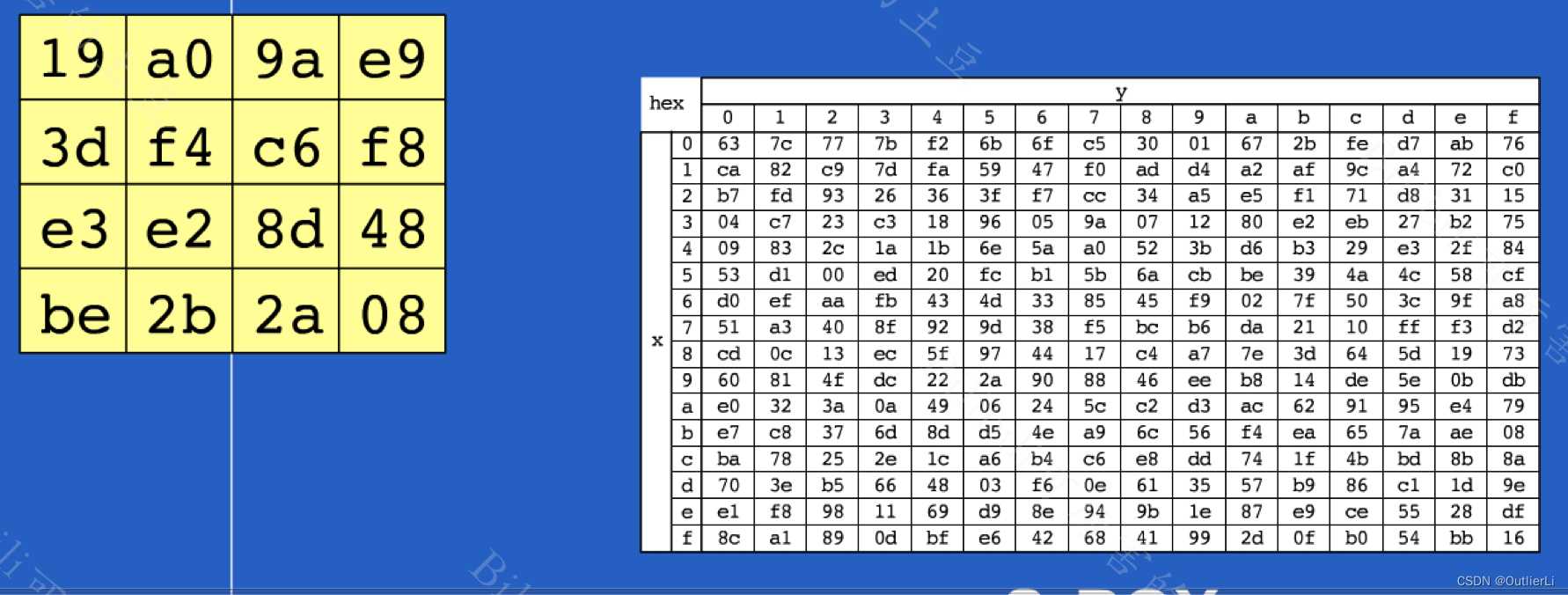
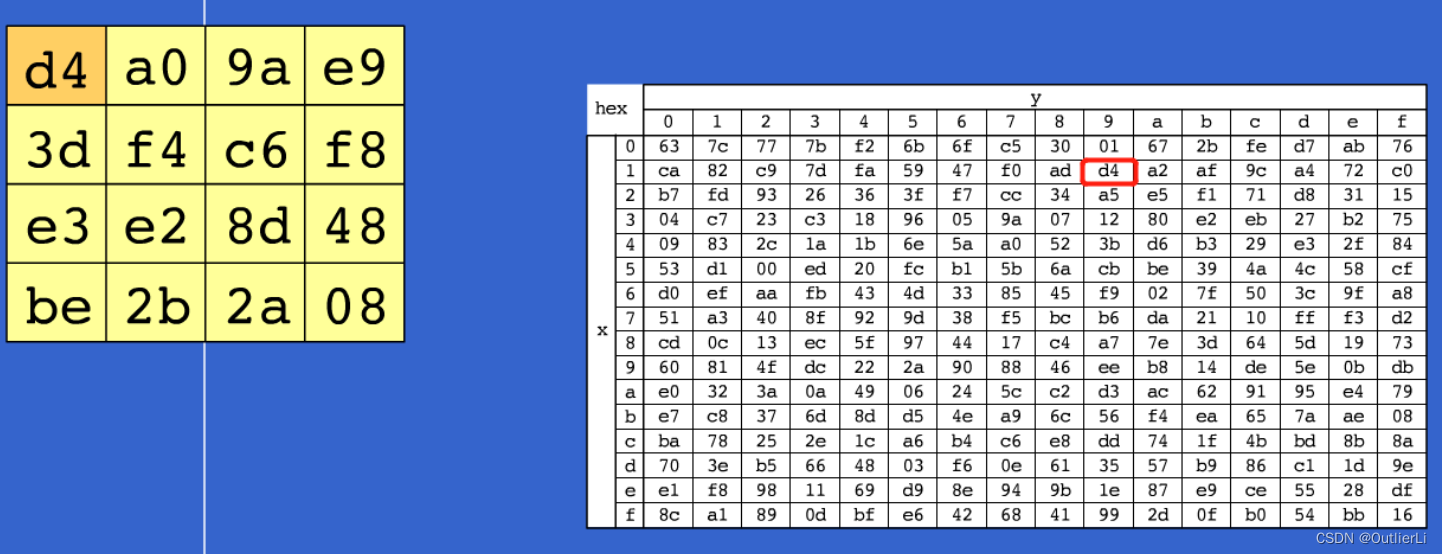
字节代换就是将矩阵(本实验中用数组模拟)中的每一个元素通过查表(查Sbox表)获取对应值进行代换;
如上图,矩阵中的第一个元素 0 X 19 0X19 0X19,高位为 1 1 1,低位为 9 9 9,查表即查找第1行,第九列的值,由图得该值为 d 4 d4 d4,所以将原矩阵中的 19 19 19换为 d 4 d4 d4;
实现过程:
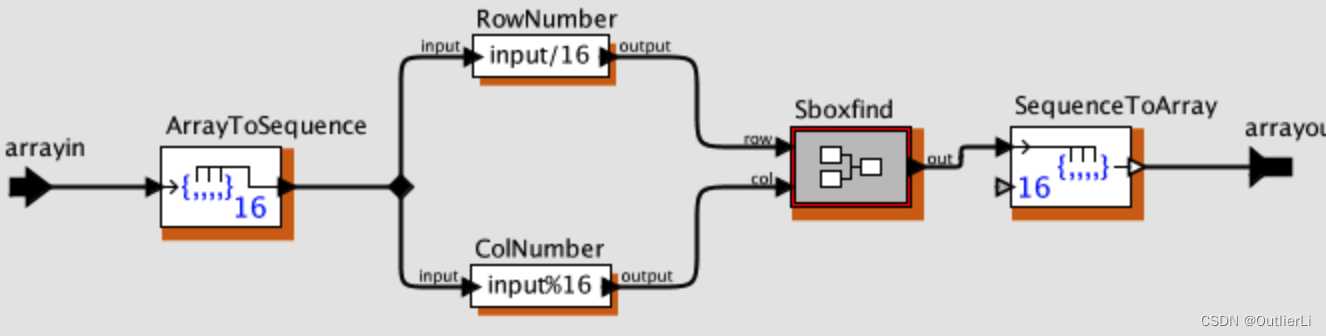
首先我们要知道行和列的序号,由于数组中元素在实际使用过程中会自动转换为10进制,所以我们要通过10进制,计算2位16进制数的高位和低位,作为Sbox的行和列;
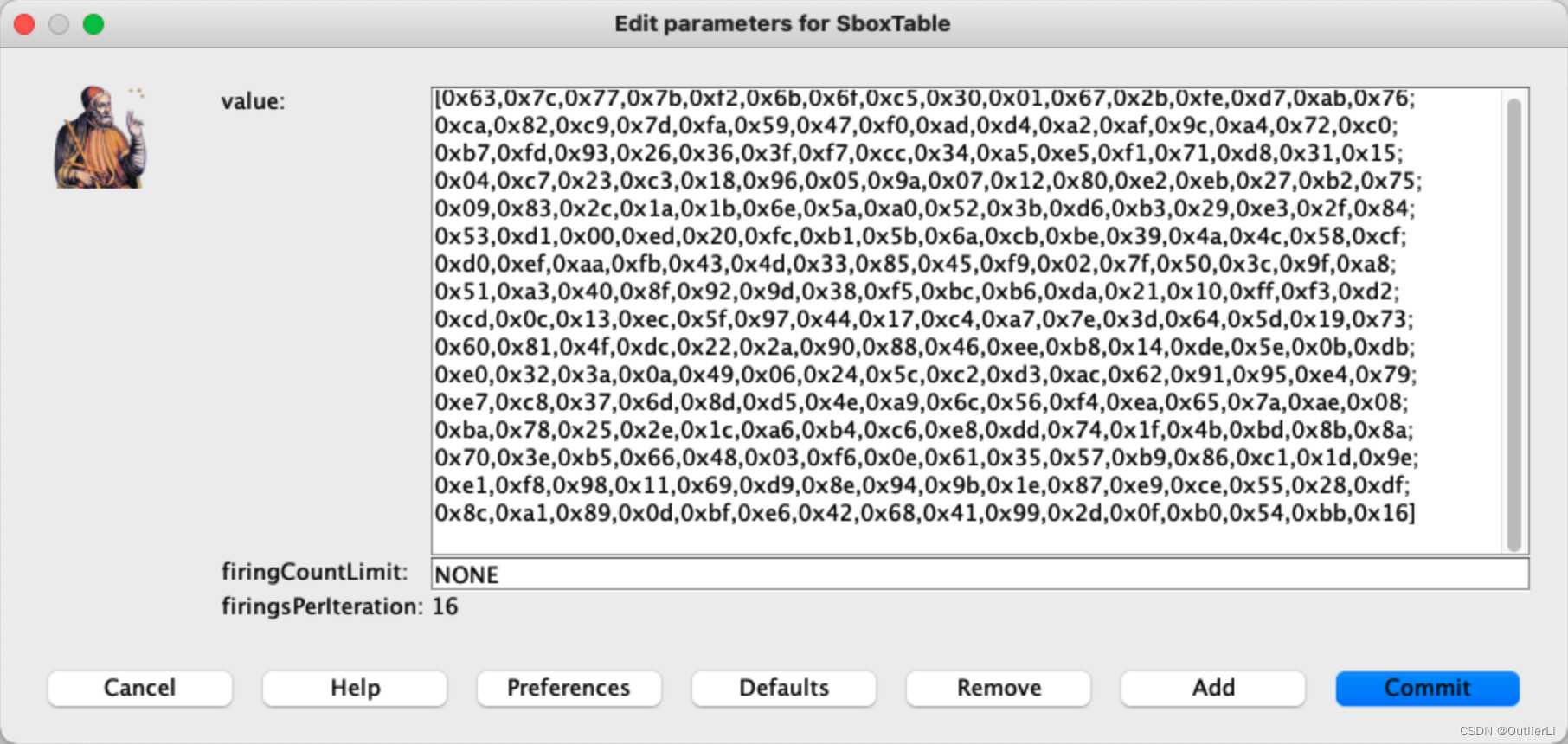
知道了行和列之后要做的就是保存Sbox表;Sbox表是一个固定的表,所以我们需要一个数据结构来存储这张表的数据,我们需要一个可以通过行和列来定位的数据结构,很显然选择矩阵;我们采用const常量来存储Sbox表的矩阵形式;
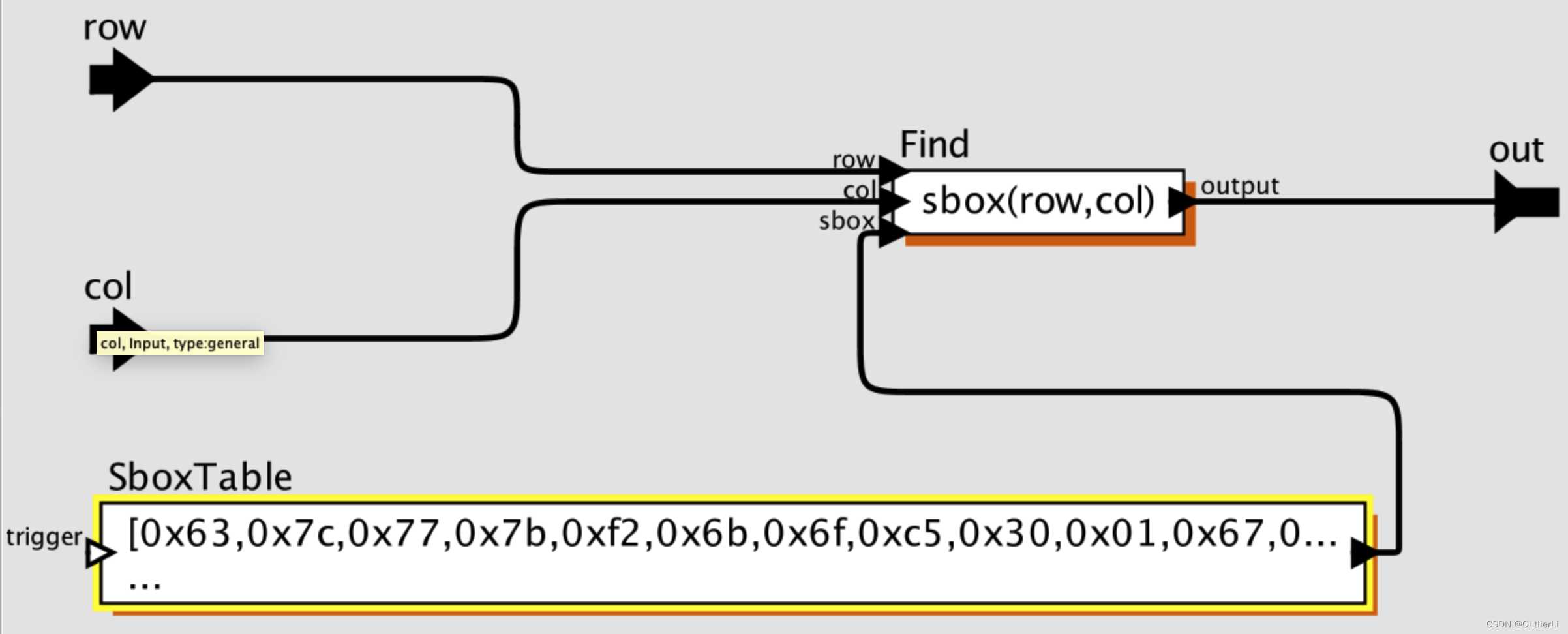
接下来就是组合上述两个模块,并用PtolemyII内置的查找矩阵元素的方法来实现查表功能;
如上图,查矩阵只需要用“矩阵名(行索引,列索引)”的表达式,即可在传入行索引、列索引、矩阵之后,传出对应位置的元素;
四、行移位(ShiftRows):
原理分析:
行位移的规则:
- 保持第一行不变;
- 第二行向左移动1个字节;
- 第三行向左移动2个字节;
- 第四行向左移动3个字节;
行位移的结果实质就是矩阵中元素位置的互换,即数组元素位置互换;实现行位移就是要实现数组元素位置互换;
具体实现:
PtolemyII中内置的extract函数可以根据数组索引提取数组元素并放置在一个新数组中;例如: { 1 , 2 , 3 } . e x t r a c t ( { 0 , 0 , 1 , 1 , 2 , 2 } ) = { 1 , 1 , 2 , 2 , 3 , 3 } \{1,2,3\}.extract(\{0,0,1,1,2,2\})=\{1,1,2,2,3,3\} {
1,2,3}.extract({
0,0,1,1,2,2})={
1,1,2,2,3,3};
原始矩阵从上到下,从左到右转换成数组为 { p 1 , p 2 , p 3 , . . . , p 1 6 } \{p_1,p_2,p_3,…,p_16\} {
p1,p2,p3,…,p16},对应数组下标为 { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 } \{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\} {
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},行位移之后的矩阵对应元素数组下标为 { 0 , 5 , 10 , 15 , 4 , 9 , 14 , 3 , 8 , 13 , 2 , 7 , 12 , 1 , 6 , 11 } \{0,5,10,15,4,9,14,3,8,13,2,7,12,1,6,11\} {
0,5,10,15,4,9,14,3,8,13,2,7,12,1,6,11},只需要用 e x t r a c t extract extract函数,提取原数组中的元素,放置在新数组中的对应位置;
五、列混合(MixColumns):
原理分析:
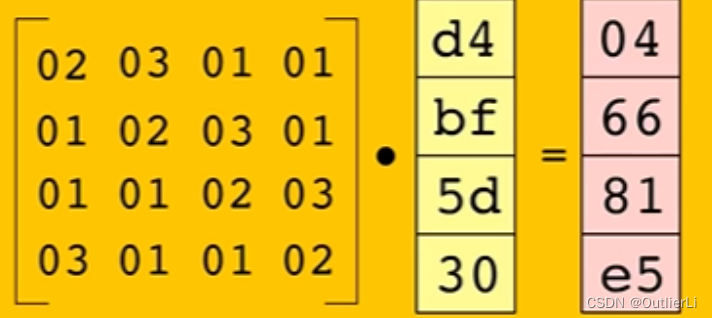
将输入的 4 ∗ 4 4*4 4∗4矩阵左乘一个给定的 4 ∗ 4 4*4 4∗4矩阵:
我们先只分析一列的情况:
由矩阵相乘的规则得, 04 = 02 ∗ d 4 + 03 ∗ b f + 01 ∗ 5 d + 01 ∗ 30 04=02*d4+03*bf+01*5d+01*30 04=02∗d4+03∗bf+01∗5d+01∗30;很显然如果是一般的乘法和加法,这个等式并不成立;事实上,此处的乘法和加法是定义在有限域上的二元运算,与普通的乘法和加法不同;
有限域上的加法:加号代表异或,即 1 + 1 1+1 1+1代表 1 x o r 1 1\ xor\ 1 1 xor 1;
有限域上的乘法:
1 1 1乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0等于 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0;
2 2 2乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0要先判断 a 7 a_7 a7,若 a 7 a_7 a7等于0,则左移一位作为结果,若 a 7 a_7 a7等于1,则左移一位后异或 00011011 00011011 00011011作为结果;
3 3 3乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0等于 2 2 2乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0后加(此处加定义为异或) 1 1 1乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0;
同理, 4 4 4乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0可以换成两个 2 2 2乘以 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0后异或;
具体实现:
左乘一个给定矩阵,由于矩阵是不变的,我们考虑采用const组件保存为常量数组类型;
观察矩阵,矩阵中元素只有三种类型: 0 X 01 , 0 X 02 , 0 X 03 0X01,0X02,0X03 0X01,0X02,0X03,为了简化模型,我们也只考虑这三种情况的乘法;
1. 被乘数为1的情况下的PtolemyII实现:
直接输入等于输出;
2. 被乘数为2的情况下的PtolemyII实现:
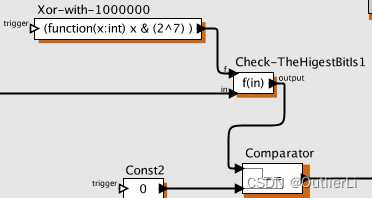
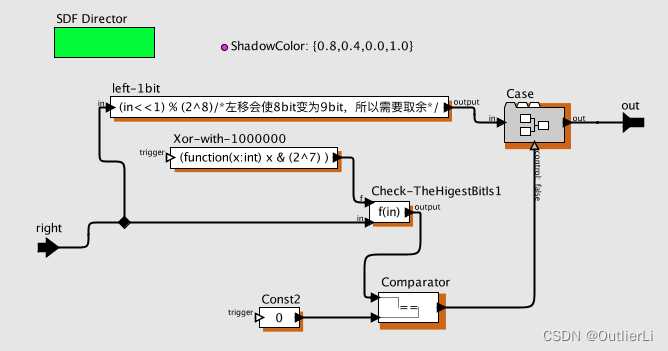
先要判断 a 7 a_7 a7的值,将 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 a_7a_6a_5a_4a_3a_2a_1a_0 a7a6a5a4a3a2a1a0按位与 1000 0000 (即 2 7 ) 1000\ 0000(即2^7) 1000 0000(即27)后判断是否为0:若结果为 T r u e True True,则说明 a 7 = 0 a_7=0 a7=0,直接左移一位后输出;若结果为 F a l s e False False则说明 a 7 = 1 a_7=1 a7=1,需要左移一位后异或 00011011 00011011 00011011;
左移操作虽然PtolemyII中有左移操作符 < < << <<,但是 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 < < 1 a_7a_6a_5a_4a_3a_2a_1a_0<<1 a7a6a5a4a3a2a1a0<<1实际上变成了 a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 a_7a_6a_5a_4a_3a_2a_1a_00 a7a6a5a4a3a2a1a00,而不是我们想要的 a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 a_6a_5a_4a_3a_2a_1a_00 a6a5a4a3a2a1a00,所以我们需要左移之后取余来去除最高位 a 7 a_7 a7;
根据 a 7 a_7 a7的值实现分支控制:
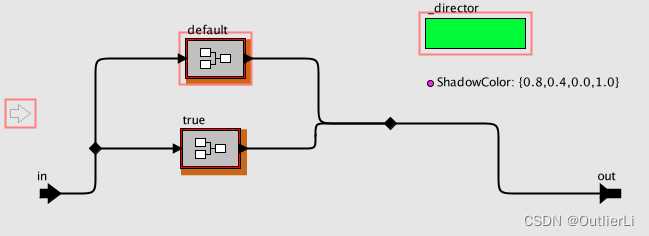
c a s e case case组件可以在SDF域上使用,实现类似select组件的选择功能;通过设置 c a s e case case的值,输入输出会进入 c a s e case case内部不同的复合组件执行;实际上就是就是选择的功能;只需要将 a 7 = = 0 a_7==0 a7==0作为控制信号,来执行 a 7 = 0 a_7=0 a7=0和 a 7 = 1 a_7=1 a7=1两种不同情况的计算;
c a s e case case组件内部:
a 7 a_7 a7为1时,执行 d e f a u l t default default组件内内容:
a 7 a_7 a7为0时,执行 t r u e true true组件内容:
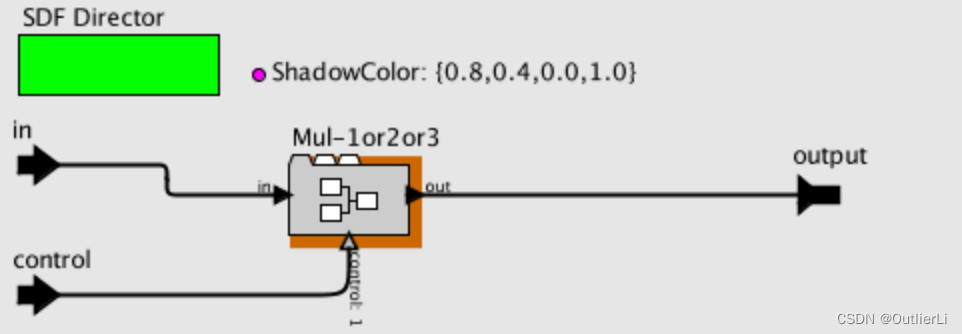
3. 被乘数为3的情况下的PtolemyII实现:
只需要组合前两种情况即可:
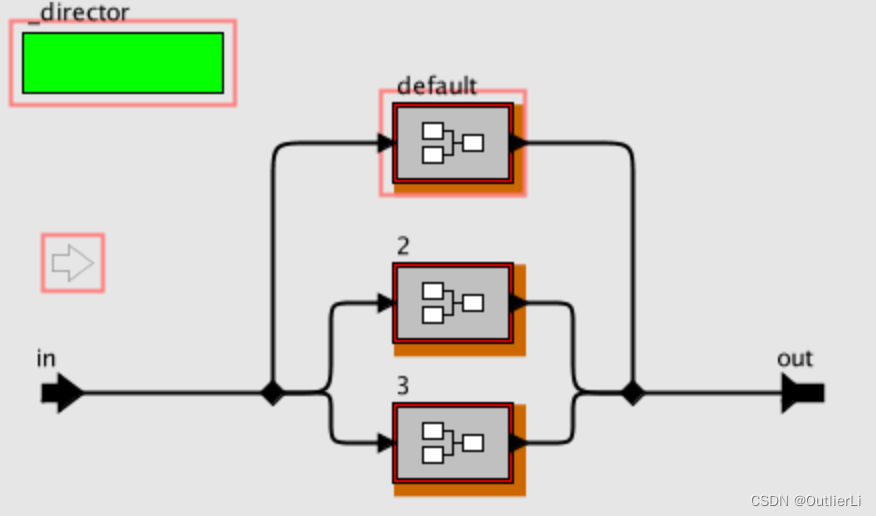
同样,采用 c a s e case case组件对三种被乘数乘法进行分支选择:
此时,我们仅仅实现了两个元素之间的,在有限域上的乘法,而下一步,我们要实现1行元素和1列元素的矩阵乘法;
而这只需要每4个元素进行一次异或就可以实现;
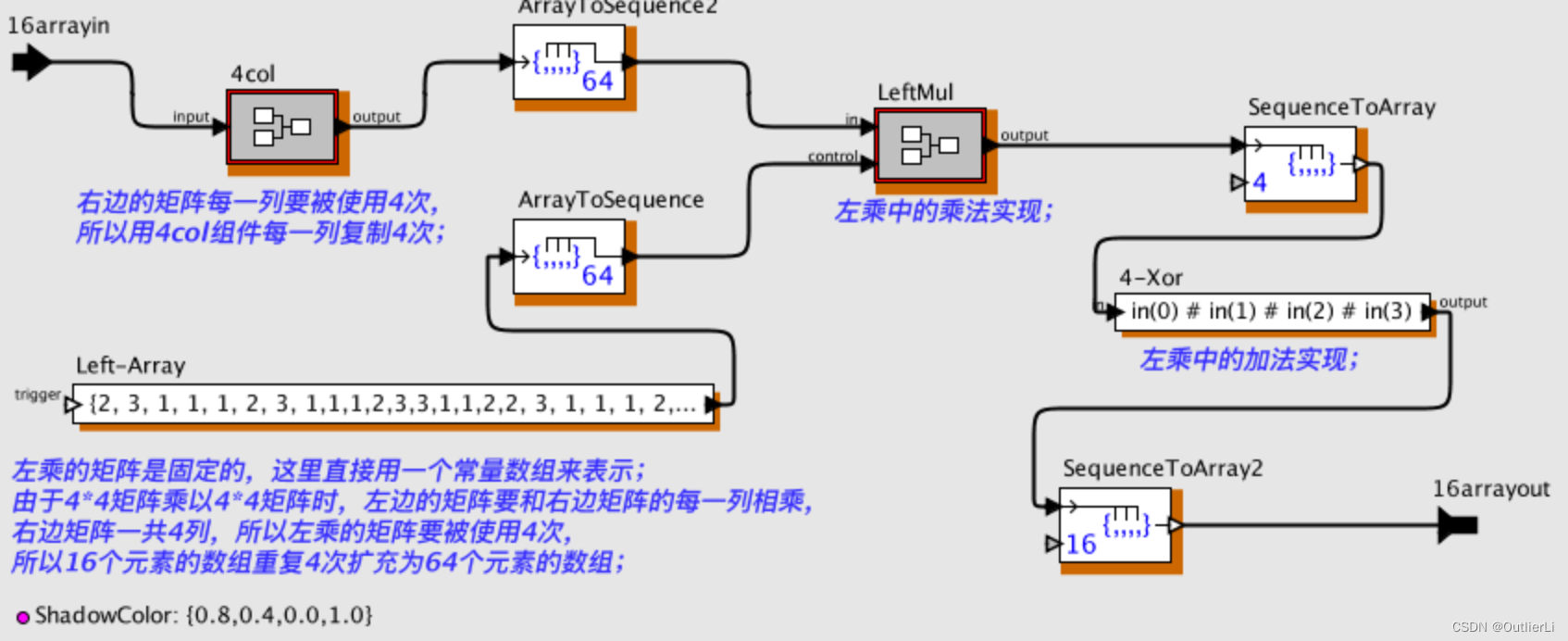
矩阵乘法中,左边矩阵每一行都要和右边矩阵的第一列相乘才能获得新矩阵的第一列,所以右边矩阵的第一列会被连续使用4次,考虑到循环可能并不容易实现,所以我们之间把右边矩阵的每一列都复制4次,然后构成新的 4 ∗ 16 4*16 4∗16的矩阵,体现为 64 64 64个元素的数组;
同样,左边矩阵要和右边矩阵的每一列都要相乘一次,一共被相乘4次,所以左边矩阵也直接整体复制4次;
如此一来,列混合就得到了实现;
六:轮密钥加(AddRoundKey):
该步的轮密钥加与第二步的轮密钥加操作过程一样,但是轮密钥发生了改变;所以完全可以复用第二步的模块,只需要添加一个轮密钥生成模块(密钥扩展);
密钥扩展:
原理分析:
很显然密钥扩展要分两种情况,假设现在时第一次轮密钥扩展,则第五列(列标号为4)可以由前4列得到的;而第六、七、八列可以由上一步得到的第五列和前四列得到;如此一来,4列的原始密钥扩展为8列,而我们只用保留后4列扩展出来的,前4列可以直接丢弃;
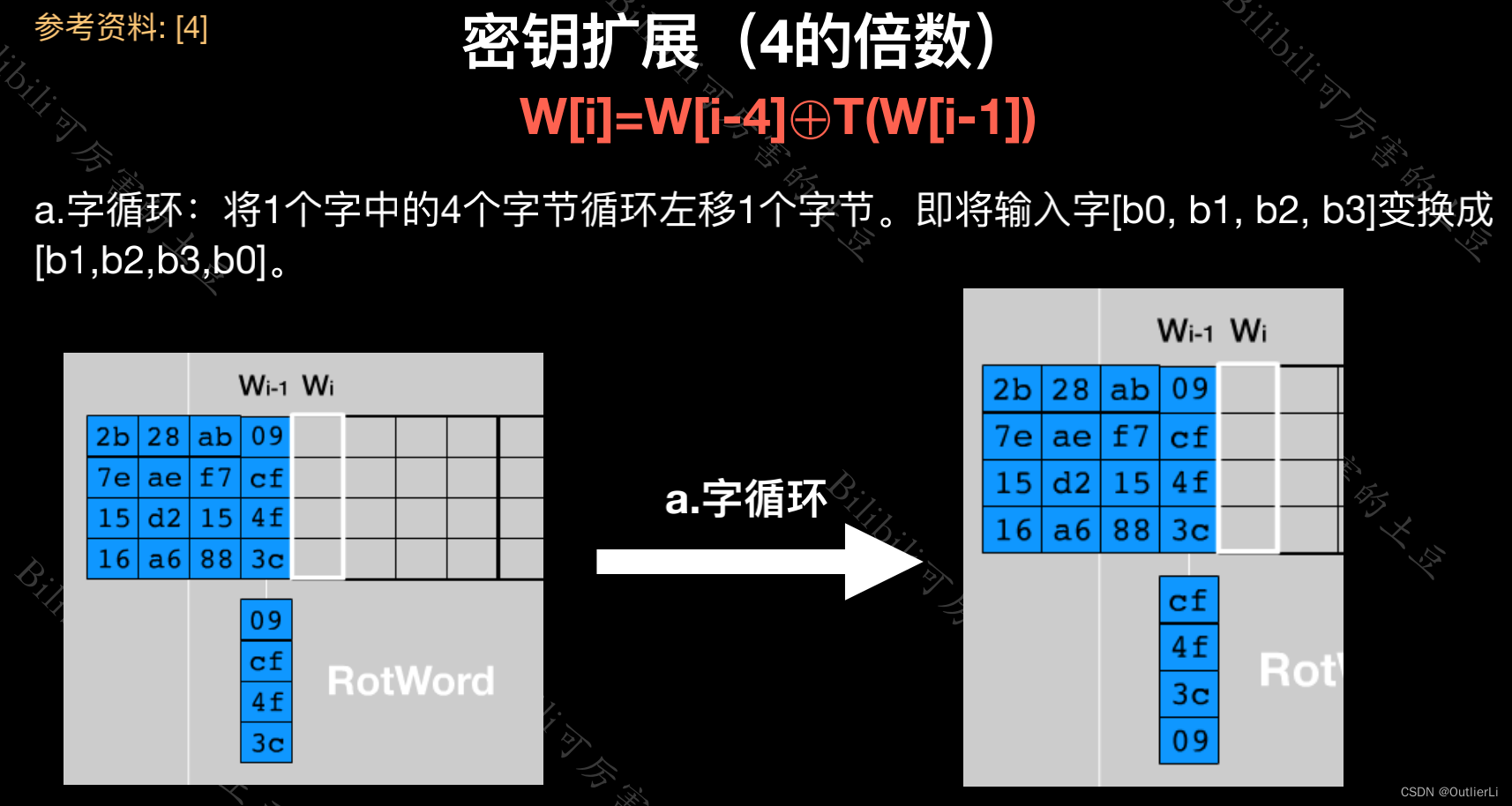
如果列标号是4的倍数时,出现了一个 T 函数 T函数 T函数, T 函数 T函数 T函数的定义如下:
字循环的实现事实上和行移位的思路一致,就是调换数组的顺序,所以直接使用 e x t r a c t ( ) extract() extract()函数;
字节代换实现思路和9轮循环中的字节替换一致,9轮循环中的字节替换是替换16字节的数组,而本次字节代换只用替换4字节;
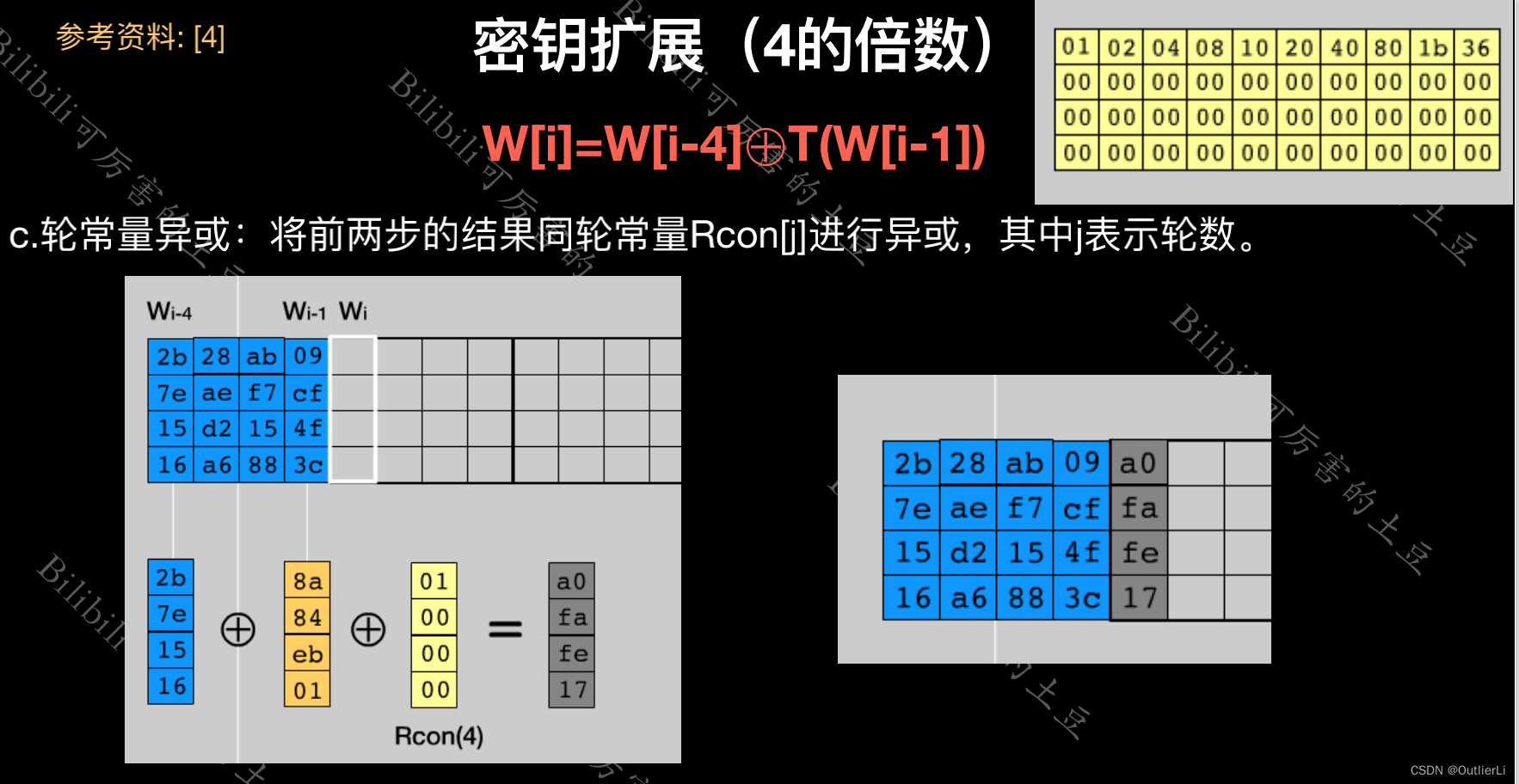
轮常量异或轮常量是固定的,所以我们可以用const组件进行保存,在需要异或时,计算出要异或的第一个元素的序号,然后依次取出一共4个元素进行异或;
具体实现:
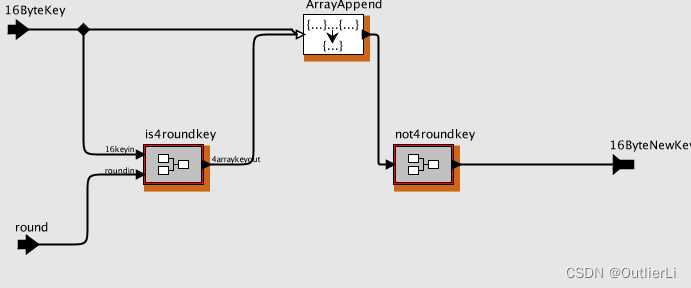
如下图,16字节的密钥先通过 i s 4 r o u n d k e y is4roundkey is4roundkey组件扩展了4字节,扩展的4字节和原始的16字节合并后通过 n o t 4 r o u n d k e y not4roundkey not4roundkey,输出16字节的扩展后的密钥;
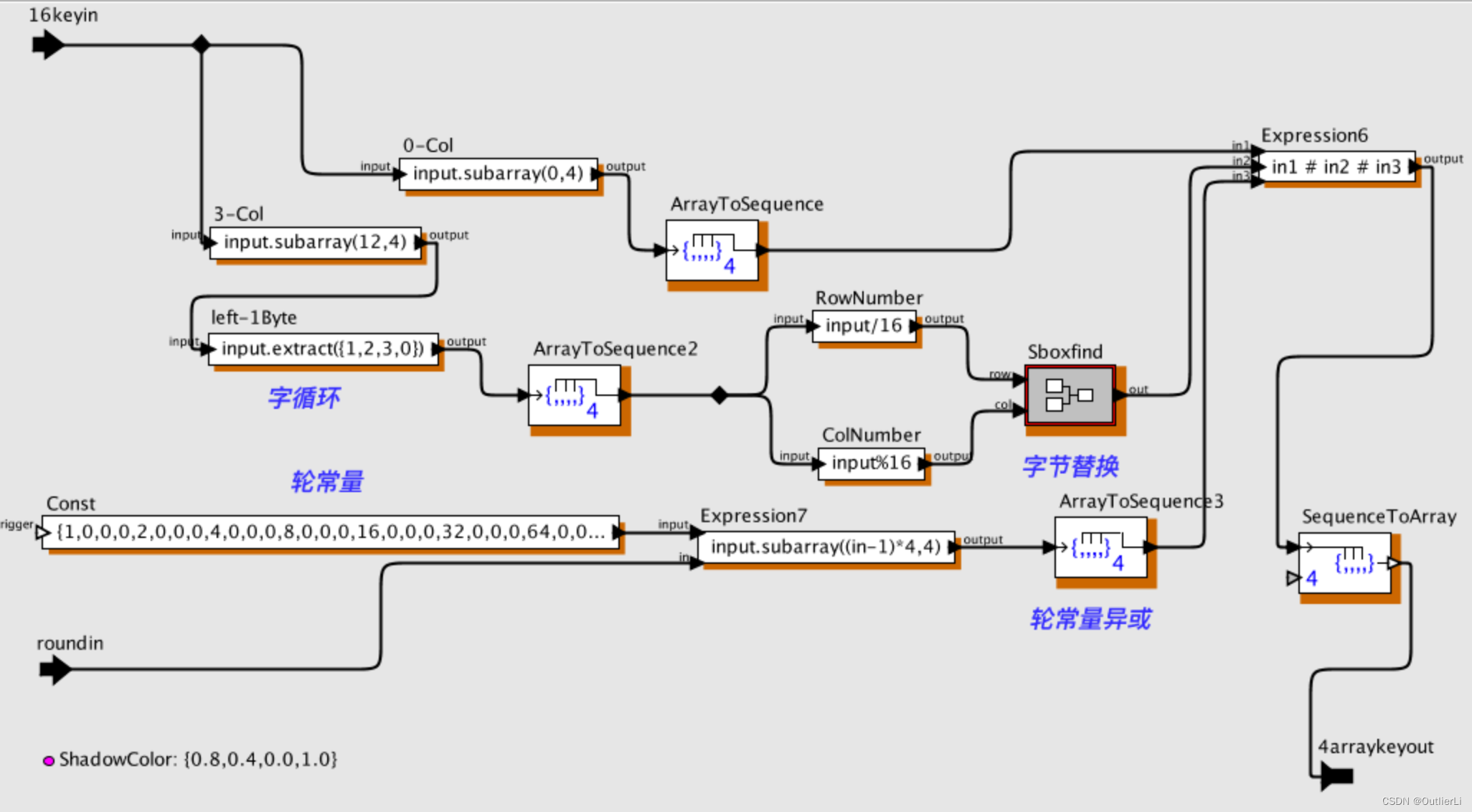
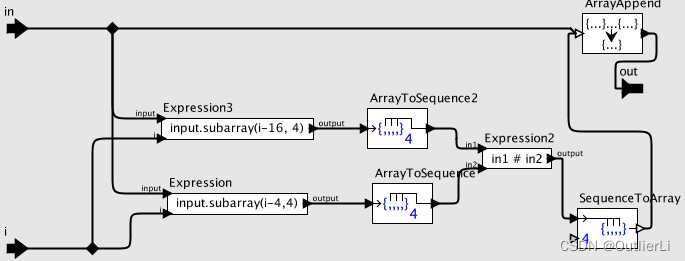
i s 4 r o u n d k e y is4roundkey is4roundkey组件内部构造如下图:
n o t 4 r o u n d k e y not4roundkey not4roundkey组件内部构造如下图:
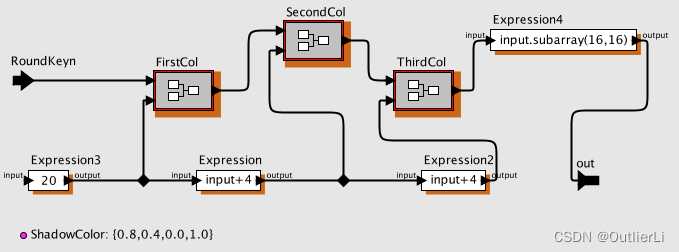
FirstCol和SecondCol和ThirdCol组件结构相同,扩展密钥的后三列分别由这三个组件完成,主要功能是取出两列异或后输出,内部构造如下图:
各个模块的功能基本已经实现,组织这些模块可以使用模态模型,模态模型内部维护一个有限状态机,而每一个模式(状态)的内部又可以细化,执行不同的功能;
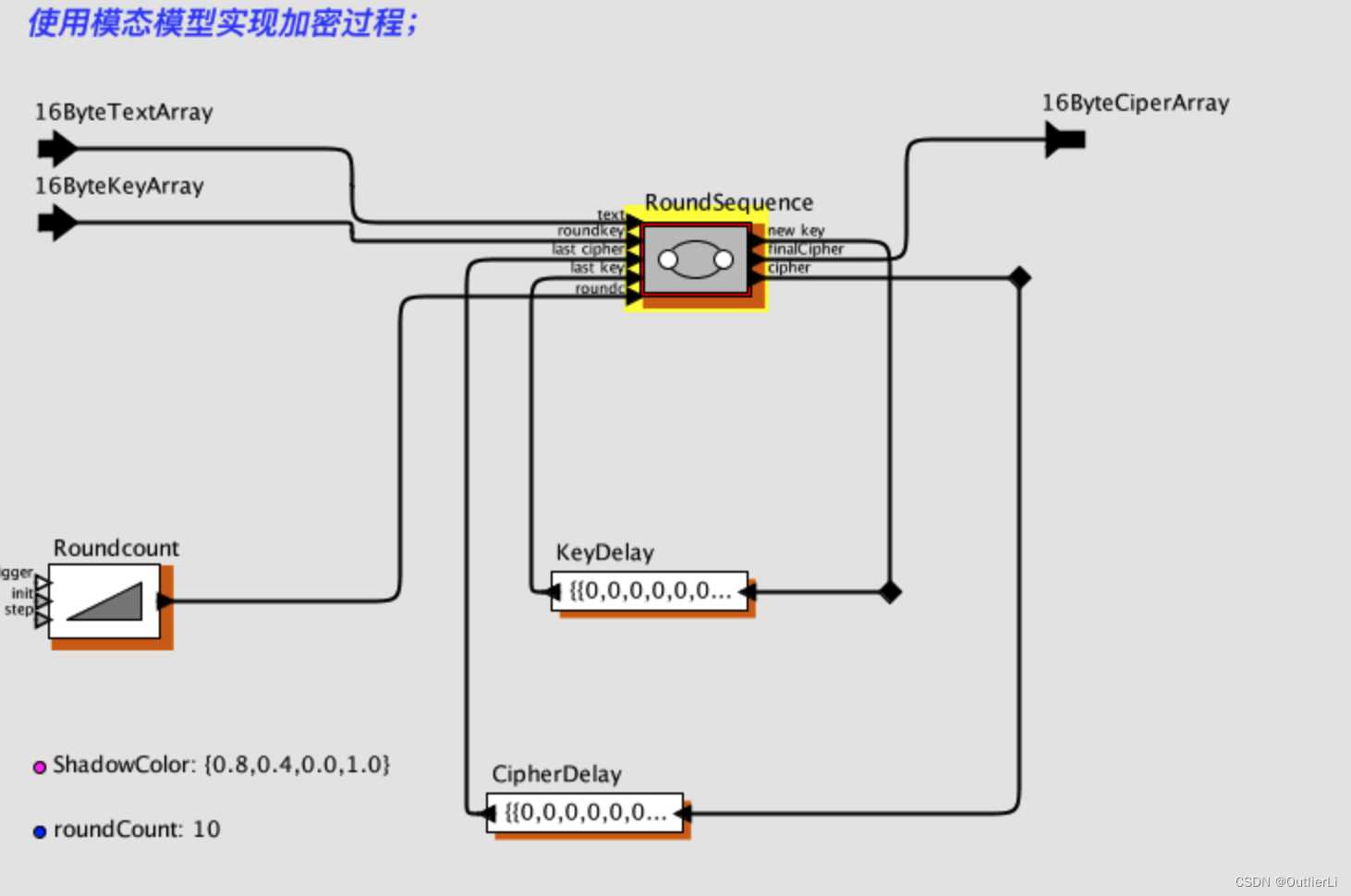
模态模型组织各模块:
上图中,模态模型 R o u n d S e q e n c e RoundSeqence RoundSeqence有五个输入端,分别输入明文、密钥、上一轮加密后的密文、下一轮的密钥,轮数;有三个输出端,分别是新密钥,最终加密的密文,本轮加密后的密文;
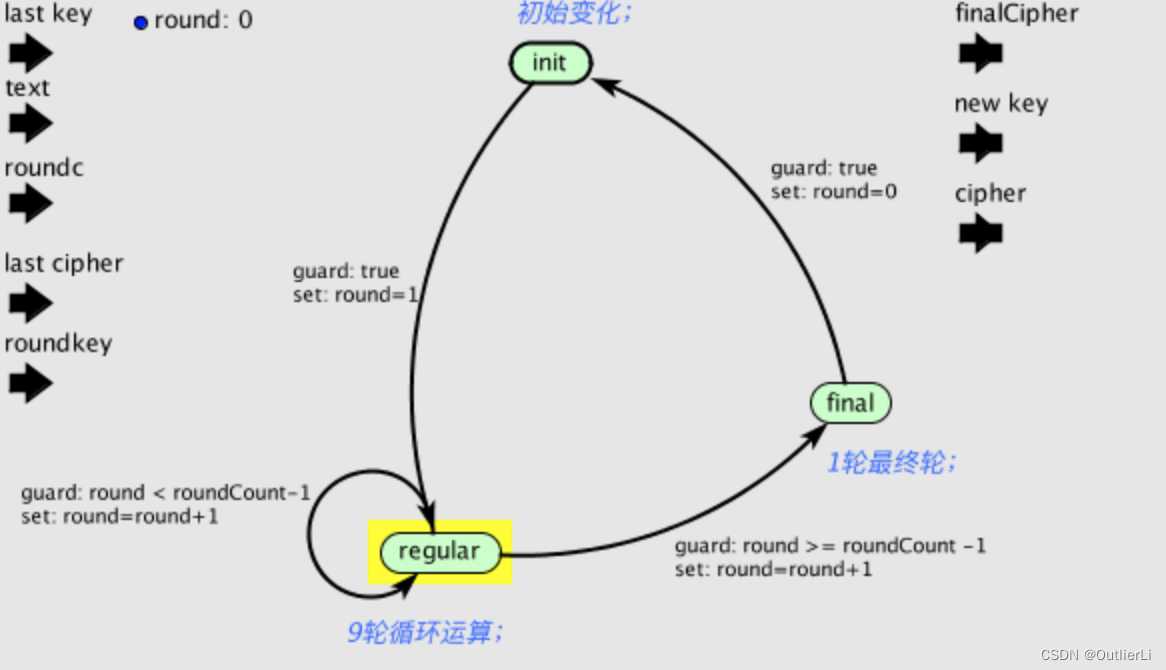
如上图, i n i t init init为初始变换, r e g u l a r regular regular代表9轮循环运算, f i n a l final final代表1轮最终轮;变量 r o u n d round round用于维护状态之间的转移;
控制和各功能模块都实现了,只需要加以组合就可以实现最终的Rijndael加密算法;
功能测试:
一组输入输出示例:
明文:{0x00,0x11,0x22,0x33,0x44,0x55,0x66,0x77,0x88,0x99,0xaa,0xbb,0xcc,0xdd,0xee,0xff}
密钥:{0x00,0x01,0x02,0x03,0x04,0x05,0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f}
密文:{“69”, “c4”, “e0”, “d8”, “6a”, “7b”, “04”, “30”, “d8”, “cd”, “b7”, “80”, “70”, “b4”, “c5”, “5a”}
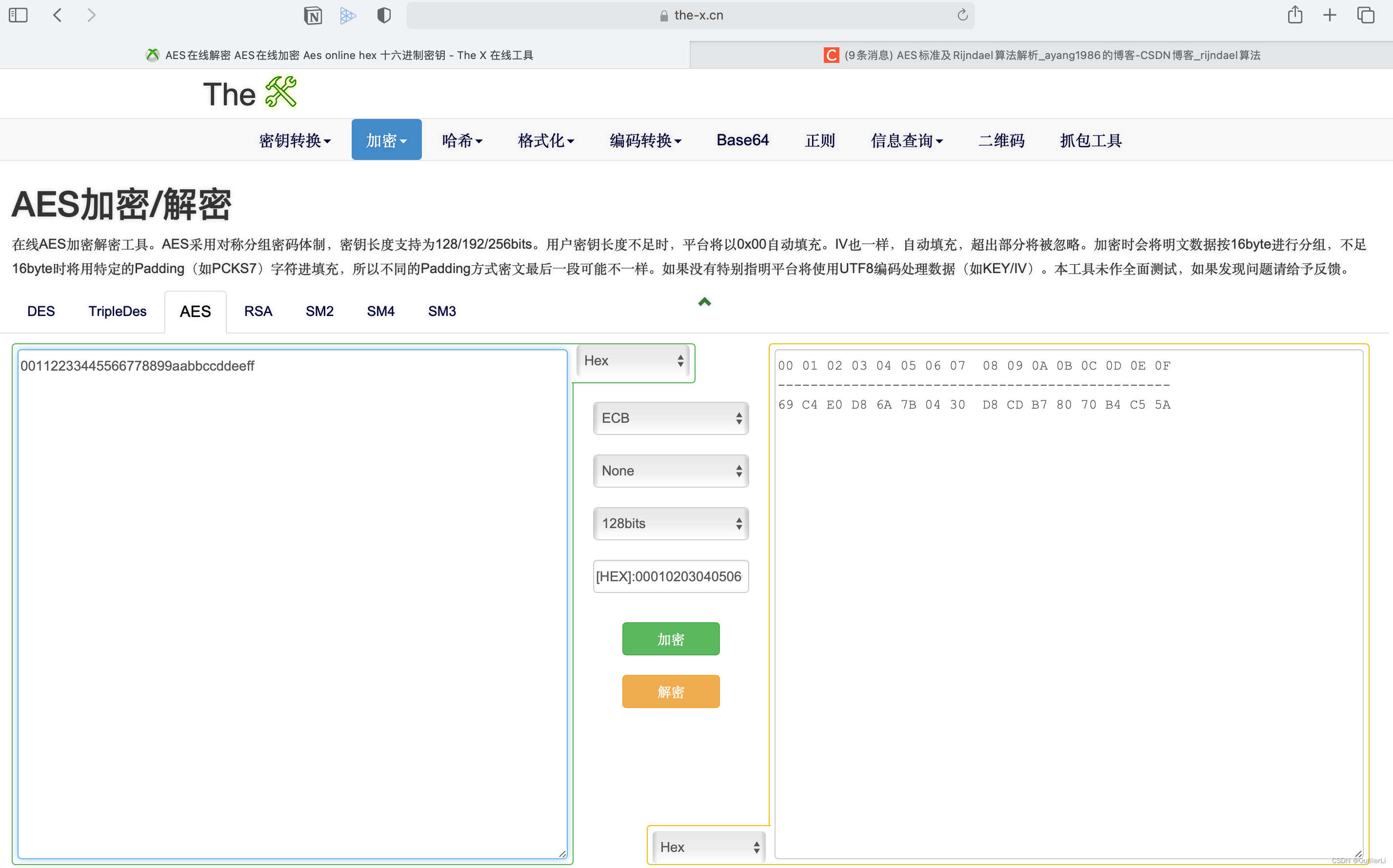
用AES在线加密工具测试:
明文:00112233445566778899aabbccddeeff
密钥:000102030405060708090a0b0c0d0e0f
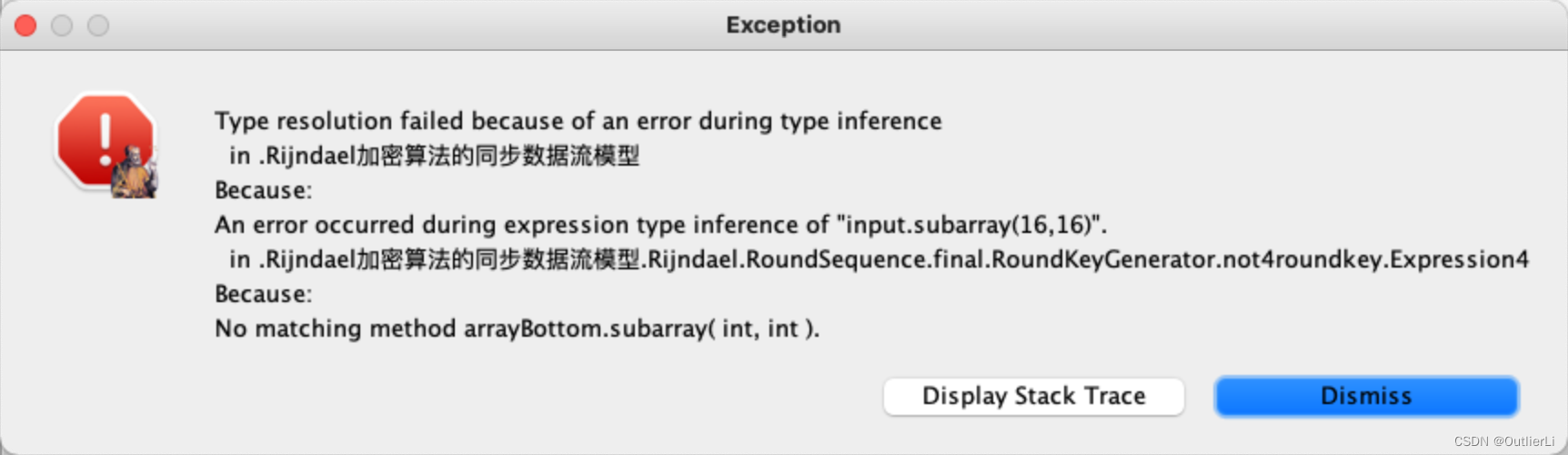
报错:
在文件打开之后第一次运行时可能会出现上图的报错,但是在关闭文件,重新打开之后该报错消失,可以正常执行;可能是源文件放的目录位置不对;可以放在bin目录下;
参考资料:
AES加密算法-Bilibili-可厉害的土豆
AES加密算法详解- CSDN
《信息物理融合系统(CPS)设计、建模与仿真》
源代码:https://github.com/OutlierLi/–Rijndael-
今天的文章信息加密领域算法_非对称加密算法有哪些分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87803.html