用cramer法则解线性方程组_jacobi迭代法求解线性方程组

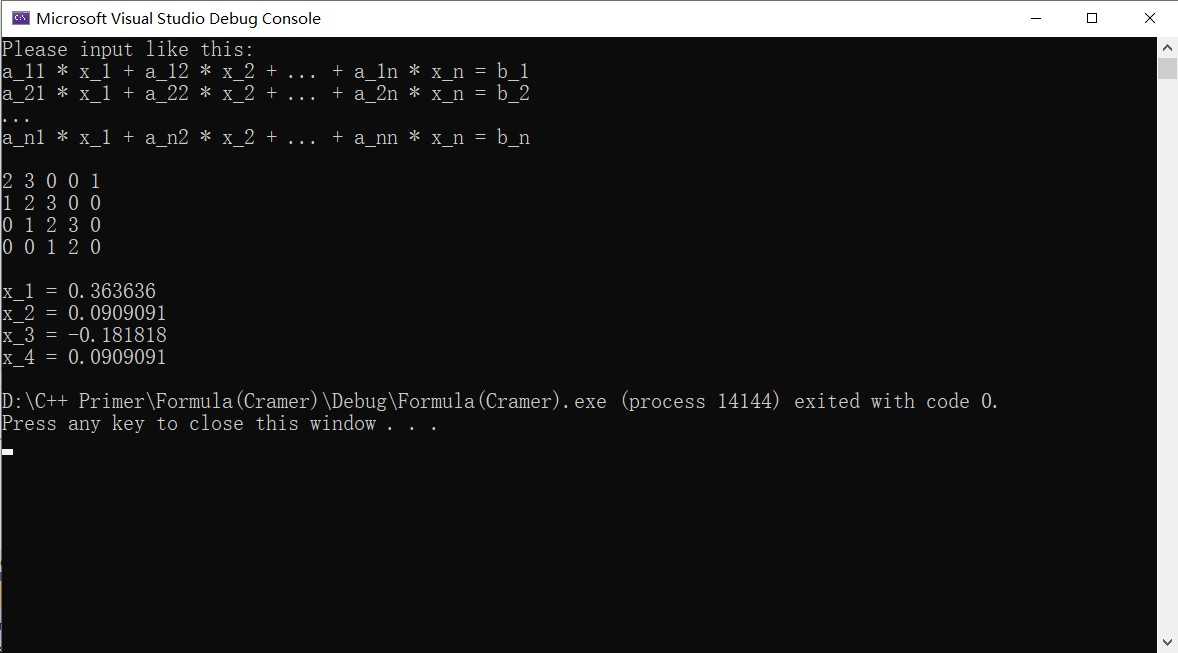
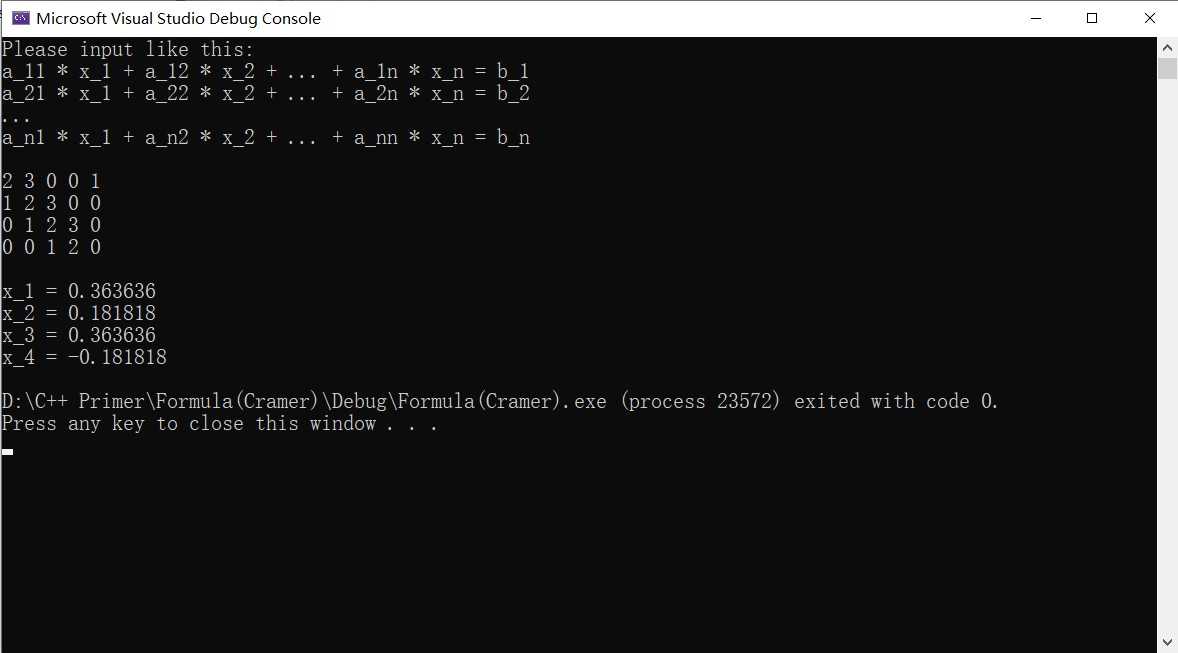
求解结果为小数。结果为分数和小数兼容的程序详见我的博客 【C++ 程序】 解线性方程组（Cramer法则）（分数形式结果）。

程序

Source.cpp

#include <iostream>
#include "Det.h"
using namespace std;

int main()
{ 
   
	int num;
	unsigned m = 0;
	deque<deque<double>> mat;
	deque<deque<deque<double>>> D;

	// instruction
	cout << "Please input like this:\n"
		<< "a_11 * x_1 + a_12 * x_2 + ... + a_1n * x_n = b_1\n"
		<< "a_21 * x_1 + a_22 * x_2 + ... + a_2n * x_n = b_2\n"
		<< "...\n"
		<< "a_n1 * x_1 + a_n2 * x_2 + ... + a_nn * x_n = b_n"
		<< "\n" << endl;

	// input
	while (1)
	{ 
   
		deque<double> row;
		while (cin >> num)
		{ 
   
			row.push_back(num);
			if (getchar() == '\n') break;
		}
		mat.push_back(row);
		m = (row.size() > m) ? row.size() : m;
		if (mat.size() >= m - 1) break;
	}

	// calculate & print
	for (unsigned i = 0; i < m; i++)
	{ 
   
		deque<deque<double>> temp = mat; // D[m - 1][m]
		for (unsigned j = 0; j != m - 1; j++)
		{ 
   
			if (i) temp[j][i - 1] = mat[j][m - 1];
			temp[j].pop_back();
		}
		D.push_back(temp);
	}
	double D0 = det_is(D[0]);
	if (D0 != 0)
	{ 
   
		cout << endl;
		for (unsigned i = 1; i < m; i++)
		{ 
   
			cout << "x_" << i << " = " << det_is(D[i]) / D0 << endl;
		}
	}
	else cout << "\nNo finite solution!" << endl;
	return 0;
}

Det.h
见我的博客 【C++ 程序】 行列式。

输出示例

分析

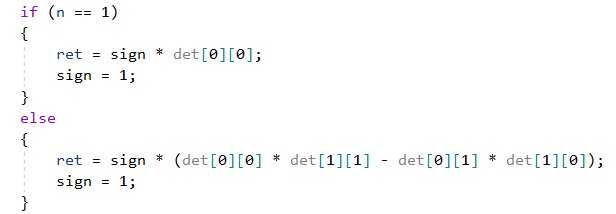
• 一开始老是错：
  

查了半天发现错误在头文件中：

一开始一直没加sign = 1的语句，造成了全局变量sign一直处于一个错误的位置。
启示：每一次调用头文件函数时，并不是重新运行的！运行一次造成的影响会带给下一次运行。

• 这里面运用到行列式的求法。
• （其他分析以后继续）

ALL RIGHTS RESERVED © 2020 Teddy van Jerry
欢迎转载，转载请注明出处。

See also

Teddy van Jerry 的导航页

今天的文章用cramer法则解线性方程组_jacobi迭代法求解线性方程组分享到此就结束了，感谢您的阅读。